P7706 文文的摄影布置 题解
读完题,发现是线段树。单点修改+区间查询。
不过查询的值有些奇怪,就是了,我们考虑用线段树维护这个 ψ 值(下称待求值)。
对于一个区间的待求值,大概有四种情况:
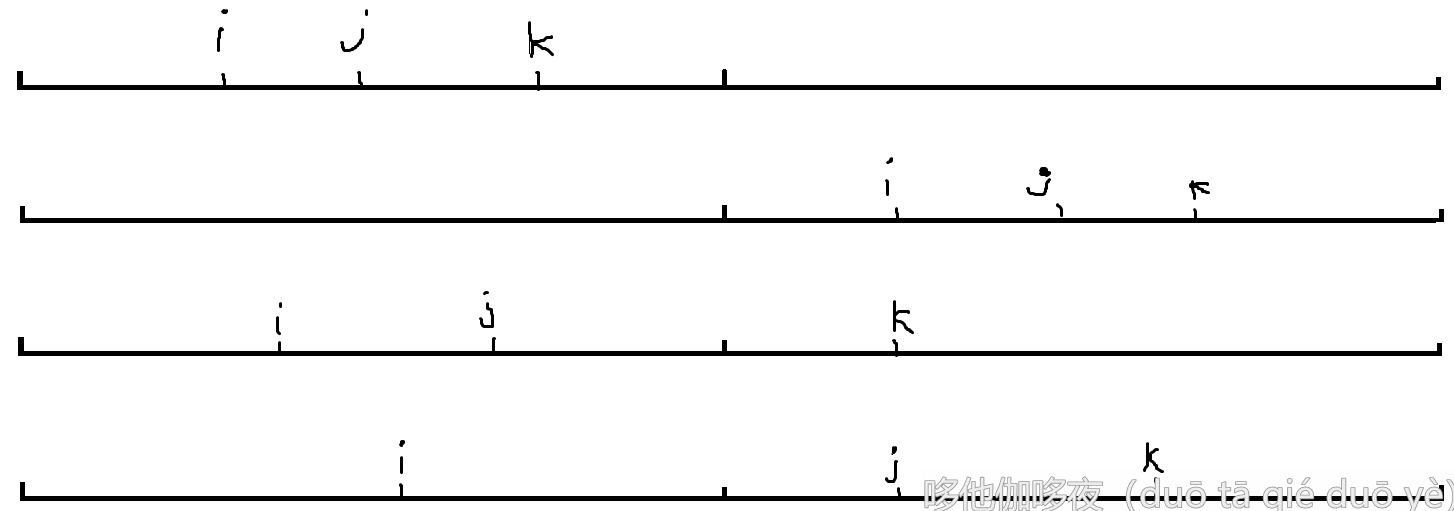
如上图四种情况分别为:
- 待求值最大值在左区间
- 待求值最大值在右区间
- \(a_i与b_j\) 在左区间
- \(b_j与a_k\) 在右区间
考虑合并的方式:
对于1,2,返回左右区间的较大的待求值。
对于3,4,维护左右区间的 \(lt\) 与 \(rt\) ,分别代表,较大的 \(a_i-b_j\) 及 较大的 \(a_k-_j\) ,更新时加上另一侧较大值即可。
由此,得出线段树结构体需要维护的值有:\(maxx,minn,lt,rt,mx\) ,分别为最大的 \(a\) ,最小的 \(b\) ,较大的 \(a_i-b_j\) 及 较大的 \(a_k-_j\) ,和本区间的最大待求值。
于是可得代码:
cpp
#include <bits/stdc++.h>
#define seq(q, w, e) for (int q = w; q <= e; q++)
#define ll long long
using namespace std;
const int maxn = 5e5+10;
const ll inf=-1e8-10;
struct pect{
ll s,b; //存图片
}a[maxn];
struct node{
ll maxx,minn; //maxx为区间a最大,minn为区间b最小
ll lt,rt,mx; //lt为区间 min(bj)-ai,rt为区间 ak-min(bj)
}tree[maxn<<2];
ll ls(ll p){return p<<1;}
ll rs(ll p){return p<<1|1;}
node up_date(node a,node b){
node p;
p.maxx=max(a.maxx,b.maxx);
p.minn=min(a.minn,b.minn);
p.lt=a.maxx-b.minn;
p.rt=b.maxx-a.minn;
p.lt=max(p.lt,max(a.lt,b.lt)); //三种情况取最大
p.rt=max(p.rt,max(a.rt,b.rt));
p.mx=max(a.lt+b.maxx,b.rt+a.maxx); //情况取最大
p.mx=max(p.mx,max(a.mx,b.mx));
return p;
}
void push_up(ll p){
tree[p]=up_date(tree[ls(p)],tree[rs(p)]);
}
void build(ll p,ll pl,ll pr){
if(pl==pr){
tree[p].maxx=a[pl].s;
tree[p].minn=a[pl].b;
tree[p].lt=tree[p].rt=tree[p].mx=inf;
return;
}
ll mid=(pl+pr)>>1;
build(ls(p),pl,mid);
build(rs(p),mid+1,pr);
push_up(p);
}
void change(ll x,ll d,ll p,ll pl,ll pr,ll op){
if(pl==pr){
if(op==1) tree[p].maxx=d;
if(op==2) tree[p].minn=d;
return;
}
ll mid=(pl+pr)>>1;
if(x<=mid) change(x,d,ls(p),pl,mid,op);
else change(x,d,rs(p),mid+1,pr,op);
push_up(p);
}
node query(ll l,ll r, ll p,ll pl,ll pr){
if(l<=pl&&r>=pr)
return tree[p];
ll mid=(pl+pr)>>1;
if(l>mid) return query(l,r,rs(p),mid+1,pr);
if(r<=mid) return query(l,r,ls(p),pl,mid);
return up_date(query(l,r,ls(p),pl,mid),query(l,r,rs(p),mid+1,pr));
}
ll n,m,op;
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m;
seq(i,1,n){
cin>>a[i].s;
}
seq(i,1,n){
cin>>a[i].b;
}
build(1,1,n);
while(m--){
int x,y;
cin>>op>>x>>y;
if(op==1){
change(x,y,1,1,n,1);
}
if(op==2){
change(x,y,1,1,n,2);
}
if(op==3){
cout<<query(x,y,1,1,n).mx<<endl;
}
}
return 0;
}