一、一览
二、遗传算法流程
**种群初始：**随机生成一组N个DNA，每个DNA上都有S个基因，每个DNA都有自己的r值（适度值）。r最大的DNA为种群最优。
**选择操作：**将每个DNA的r值占总体的比例作为新一代选取的概率，再生成一组N个DNA，这些DNA都是从种群的概率选取来的。例如：上一代3号DNA的r3值占总r值为r3/r=1/6，则这一代中3号DNA就有大约1/6N个。
**交叉操作：**选择相邻的两个DNA，随机选择某段基因进行等位交换，让新的种群有更多的DNA样本。交叉率较高。
**变异操作：**随机选择DNA的某段基因进行变异。变异率较低。
三、算法介绍
3.1编码、解码
本文用一元函数模拟在指定区间求最值，函数y=f(x),x∈lower,upper，保留Accuracy位小数点精度，可将区间划分(upper-lower)*10^Accuracy等份，因为需要用二进制编码，所以编码长度n=Log2((upper-lower)*10^Accuracy)，此编码实质是将区间lower,upper内对应的实数x转化为一个二进制串：
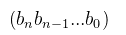
例如，保留精度6位，区间-1,2，则串长n=22
我们知道不管是int类型还是long类型，我们可以直接转二进制，而且二进制的长度可以计算，如下：
但是，对于函数y=f(x),x∈lower,upper，区间是未知的，说明有可能为负号，且对于实数x而言，在设计的时候为了追求精度，可能设计成单精度或双精度，那么该如何编码或解码？如何利用到上面已知的编码、解码方式？
我们知道数据很大的时候一般会把数据01化，如下公式：
这样的话就可以把实数x经过g(x)映射到0,1内，记为x->g(x)，以就成了正数，但是还没有达到整数。
对于函数y=f(x)，x∈lower,upper，我们一般需要保留n位小数，那么我们就可以把g(x)扩大10^n 倍，为了统一编码长度，就应该扩大(upper-lower)*10^n 倍。
此时二进制串的长度=log2((upper-lower)*10^n)，值x->G(x)=g(x)*(upper-lower)*10^n ,这样既保证了长度，也保证了符号。（这里的n指精度）
代码实现
geneMinLength指二进制串长度，代码如下：
3.2种群初始化
PopulationSize为种群大小，在区间lower,upper上随机生成实数x，然后编码、计算适应度值，如下：
3.3选择操作
我们将r值（适应度值）所占总体的比例计算出来，然后利用累积概率随机选择DNA。r值（适应度值）所占总体的比例越大，越容易被选择。选择操作时保留精英代，下一次操作直接加入种群。
3.4交叉操作
3.5变异操作：
这里采用多点变异，变异时直接取反，例如：0->1，1->0
3.6适应度函数
适应度函数采用目标函数+指数函数，如下：
这里采用目标函数外，为什么还需要用指数函数？因为我们在选取时，需要适应度为正数且函数值有正负，例如在指定区间找最小值，越小的值(有正负)，指数函数(0<a<1)映射的值越大，以就是权重越大，被选择的概率就越大。
指数函数：
经过一次迭代后再次回到3.3选择操作，直到迭代结束。
迭代代码如下：
这里种群大小为50，迭代200，交叉率0.75，变异率0.05作为测试。