输入序列连续的序列检测
描述
请编写一个序列检测模块,检测输入信号a是否满足01110001序列,当信号满足该序列,给出指示信号match。
模块的接口信号图如下:

模块的时序图如下:

请使用Verilog HDL实现以上功能,并编写testbench验证模块的功能
输入描述:
clk:系统时钟信号
rst_n:异步复位信号,低电平有效
a:单比特信号,待检测的数据
输出描述:
match:当输入信号a满足目标序列,该信号为1,其余时刻该信号为0
解题思路
思路一:经典有限状态机三段式
可设置以下状态:
IDLE(S0):初始状态,表示电路还没有收到任何一个有效数值;
S1 :表示电路收到一个有效的"0";
S2 :表示电路收到两个有效的"01";
S3 :表示电路收到三个有效的"011";
S4 :表示电路收到四个有效的"0111";
S5 :表示电路收到五个有效的"01110";
S6 :表示电路收到六个有效的"011100";
S7 :表示电路收到七个有效的"0111000";
S8 :表示电路收到七个有效的"01110001";
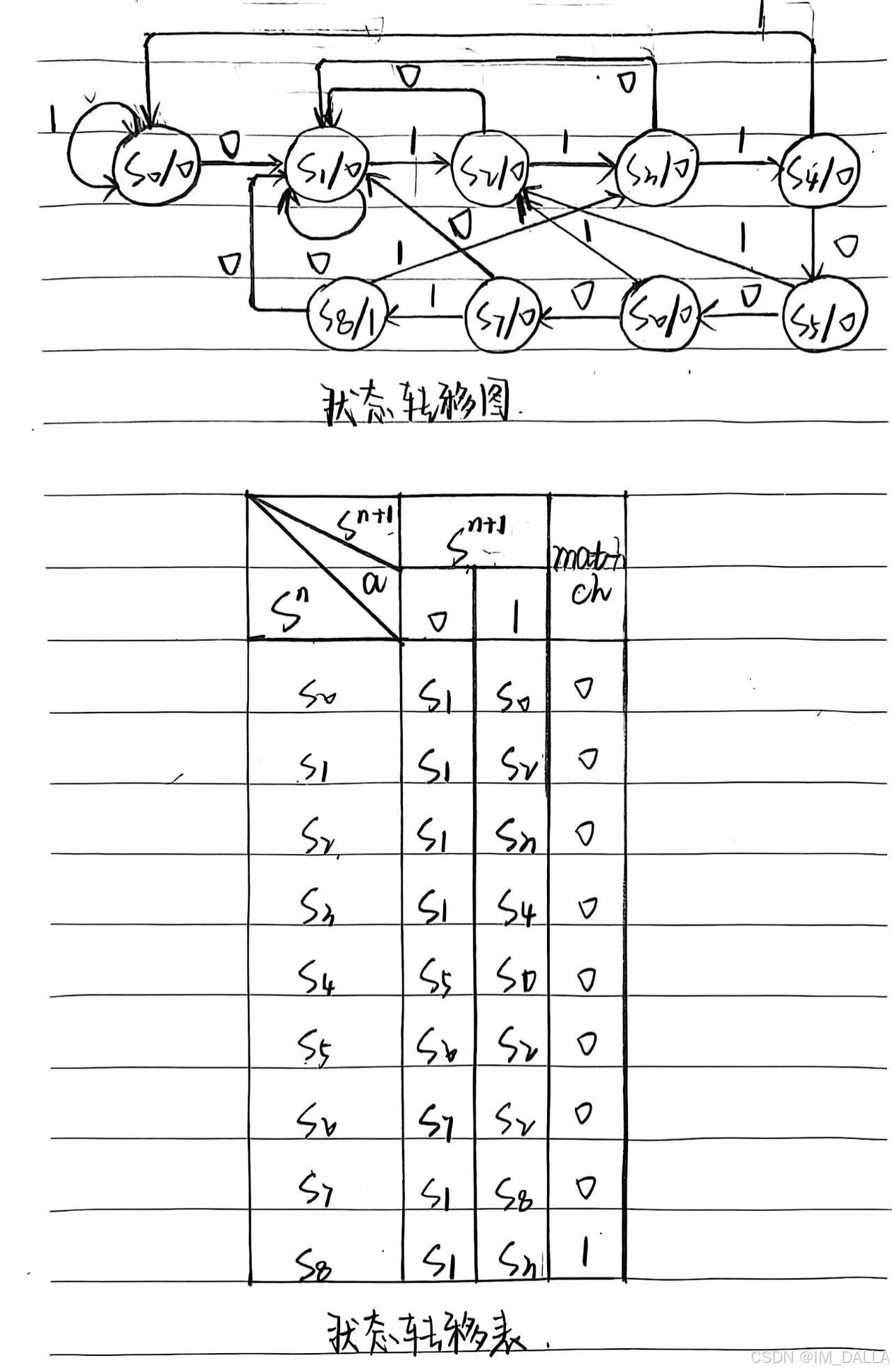
根据输出表述,"当输入信号a满足目标序列时,match信号为1," 因此可画出如下所示的状态转移图 和状态转移表;
格雷码的相关知识
++Gray码也称为循环码,++ 其最基本的特性是任何相邻的两组代码中,仅有一位数码不同 ,因而又称为单位距离码。减少了产生毛刺和一些暂态的可能。
Gray码的编码方式有多种,典型的格雷码如下所示:
|------|----|----|----|----|-------|-------|-------|-------|
| 十进制数 | 二进制码 |||| Gray码 ||||
| 十进制数 | B3 | B2 | B1 | B0 | G3 | G2 | G1 | G0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 3 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 5 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 7 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 8 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| 10 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 11 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 |
| 12 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 13 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 14 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 15 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
从上述表中可以看出,这种编码除了具有单位距离码的特点之外,还有一个特点就是具有反射特性 ;例如上表中的不同颜色的字体部分(红、蓝、橙),除最高位互补反射外,其余低位数沿对称轴镜像对称、++利用这一反射特性可以方便地构成位数不同的Gray码++;
Gray码的单位距离特性 具有很重要的意义。假如两个相邻的十进制数13和14,相应的二进制码为1101 和1110 ;若使用二进制数进行加1计数时,如果从13变成14,二进制码的最低两位都要改变,但实际上两位改变不可能完全同时发生,若先最低位置0,然后次低位再置1,则中间会出现1101-1100-1110,即++出现短暂的1100++ ;由于++格雷码只有一位编码,因此完全杜绝了这种错误的发生++;
代码如下
cpp
`timescale 1ns/1ns
module sequence_detect(
input clk,
input rst_n,
input a,
output reg match
);
reg [3:0] current_state, next_state;
//格雷码
parameter [3:0] IDLE = 4'b0000;
parameter [3:0] S1 = 4'b0001;
parameter [3:0] S2 = 4'b0011;
parameter [3:0] S3 = 4'b0010;
parameter [3:0] S4 = 4'b0110;
parameter [3:0] S5 = 4'b0111;
parameter [3:0] S6 = 4'b0101;
parameter [3:0] S7 = 4'b0100;
parameter [3:0] S8 = 4'b1100;
always @(posedge clk or negedge rst_n) begin
if (!rst_n) current_state <= IDLE;
else current_state <= next_state;
end
always @(*) begin
case(current_state)
IDLE: if (a == 1'b0) next_state = S1; else next_state = IDLE;
S1: if (a == 1'b1) next_state = S2; else next_state = S1;
S2: if (a == 1'b1) next_state = S3; else next_state = S1;
S3: if (a == 1'b1) next_state = S4; else next_state = S1;
S4: if (a == 1'b0) next_state = S5; else next_state = IDLE;
S5: if (a == 1'b0) next_state = S6; else next_state = S2;
S6: if (a == 1'b0) next_state = S7; else next_state = S2;
S7: if (a == 1'b1) next_state = S8; else next_state = S1;
S8: if (a == 1'b0) next_state = S1; else next_state = S3;
default: next_state = IDLE;
endcase
end
always @(posedge clk or negedge rst_n) begin
if (!rst_n) match <= 1'b0;
else begin
case (current_state)
IDLE: match = 1'b0;
S1: match = 1'b0;
S2: match = 1'b0;
S3: match = 1'b0;
S4: match = 1'b0;
S5: match = 1'b0;
S6: match = 1'b0;
S7: match = 1'b0;
S8: match = 1'b1;
default: match = 1'b0;
endcase
end
end
endmodule思路二:使用移位寄存器
移位寄存器可以用来实现数据的串并转换 ,也可以构成移位行计数器 ,进行计数 、分频 ,还可以构成序列码发生器、序列码检测器等,它也是数字系统中应用非常广泛的时序逻辑之一;
代码如下:
根据检测序列位数确定寄存器的位数;
cpp
`timescale 1ns/1ns
module sequence_detect(
input clk,
input rst_n,
input a,
output reg match
);
//代码二
//使用8位移位寄存器
reg [7:0] shift_q;
//注意:必须使用非阻塞赋值语句(若使用 "="会报错)
always @(posedge clk or negedge rst_n) begin
if (!rst_n) begin shift_q <= 8'b0000_0000; match <= 1'b0; end
else begin
shift_q [7:0] <= {shift_q[6:0], a};
if (shift_q == 8'b0111_0001) match <= 1'b1;
else match <= 1'b0;
end
end
endmodule