详解残差网络为什么有用?
为什么ResNets 能有如此好的表现,来看个例子,它解释了其中的原因,至少可以说明,如何构建更深层次的ResNets 网络的同时还不降低它们在训练集上的效率。通常来讲,网络在训练集上表现好,才能在Hold-Out 交叉验证集或dev 集和测试集上有好的表现,所以至少在训练集上训练好ResNets是第一步。
先来看个例子,一个网络深度越深,它在训练集上训练的效率就会有所减弱,这也是有时候不希望加深网络的原因。而事实并非如此,至少在训练ResNets网络时,并非完全如此,举个例子。
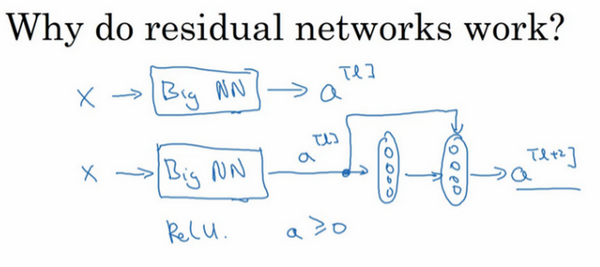
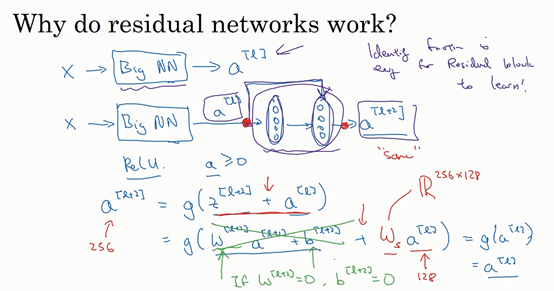
假设有一个大型神经网络,其输入为\(X\),输出激活值\(a^{[l]}\)。假如想增加这个神经网络的深度,那么用Big NN 表示,输出为 a\^{\\left\\lbrack l\\right\\rbrack}\\(。再给这个网络额外添加两层,依次添加两层,最后输出为\\)a\^{\\left\\lbrack l + 2 \\right\\rbrack}\\(,可以把这两层看作一个\*\*ResNets\*\*块,即具有捷径连接的残差块。为了方便说明,假设在整个网络中使用\*\*ReLU\*\*激活函数,所以激活值都大于等于0,包括输入\\)X的非零异常值。因为ReLU激活函数输出的数字要么是0,要么是正数。
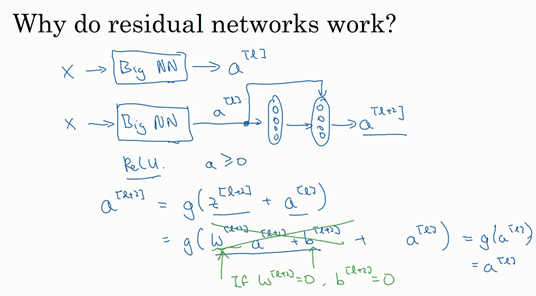
看一下\(a^{\left\lbrack l + 2\right\rbrack}\)的值,即\(a^{\left\lbrack l + 2\right\rbrack} = g(z^{\left\lbrack l + 2 \right\rbrack} + a^{\left\lbrack l\right\rbrack})\),添加项\(a^{\left\lbrack l\right\rbrack}\)是刚添加的跳跃连接的输入。展开这个表达式\(a^{\left\lbrack l + 2 \right\rbrack} = g(W^{\left\lbrack l + 2 \right\rbrack}a^{\left\lbrack l + 1 \right\rbrack} + b^{\left\lbrack l + 2 \right\rbrack} + a^{\left\lbrack l\right\rbrack})\),其中\(z^{\left\lbrack l + 2 \right\rbrack} = W^{\left\lbrack l + 2 \right\rbrack}a^{\left\lbrack l + 1 \right\rbrack} + b^{\left\lbrack l + 2\right\rbrack}\)。注意一点,如果使用L2 正则化或权重衰减,它会压缩\(W^{\left\lbrack l + 2\right\rbrack}\)的值。如果对\(b\)应用权重衰减也可达到同样的效果,尽管实际应用中,有时会对\(b\)应用权重衰减,有时不会。这里的\(W\)是关键项,如果\(W^{\left\lbrack l + 2 \right\rbrack} = 0\),为方便起见,假设\(b^{\left\lbrack l + 2 \right\rbrack} = 0\),这几项就没有了,因为它们(\(W^{\left\lbrack l + 2 \right\rbrack}a^{\left\lbrack l + 1 \right\rbrack} + b^{\left\lbrack l + 2\right\rbrack}\))的值为0。最后 a\^{\\left\\lbrack l + 2 \\right\\rbrack} = \\ g\\left( a\^{\[l\]} \\right) = a\^{\\left\\lbrack l\\right\\rbrack}\\(,因为假定使用\*\*ReLU\*\*激活函数,并且所有激活值都是非负的,\\)g\\left(a\^{\[l\]} \\right)\\(是应用于非负数的\*\*ReLU\*\*函数,所以\\)a\^{\[l+2\]} =a\^{\[l\]}。
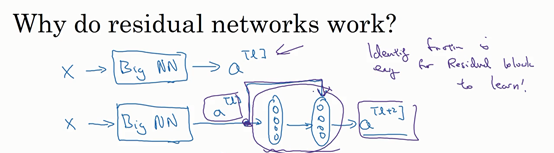

结果表明,残差块学习这个恒等式函数并不难,跳跃连接使很容易得出 a\^{\\left\\lbrack l + 2 \\right\\rbrack} = a\^{\\left\\lbrack l\\right\\rbrack}\\(。这意味着,即使给神经网络增加了这两层,它的效率也并不逊色于更简单的神经网络,因为学习恒等函数对它来说很简单。尽管它多了两层,也只把\\)a^{\[l\]}的值赋值给a^。所以给大型神经网络增加两层,不论是把残差块添加到神经网络的中间还是末端位置,都不会影响网络的表现。
当然,目标不仅仅是保持网络的效率,还要提升它的效率。想象一下,如果这些隐藏层单元学到一些有用信息,那么它可能比学习恒等函数表现得更好。而这些不含有残差块或跳跃连接的深度普通网络情况就不一样了,当网络不断加深时,就算是选用学习恒等函数的参数都很困难,所以很多层最后的表现不但没有更好,反而更糟。
认为残差网络起作用的主要原因就是这些残差块学习恒等函数非常容易,能确定网络性能不会受到影响,很多时候甚至可以提高效率,或者说至少不会降低网络的效率,因此创建类似残差网络可以提升网络性能。
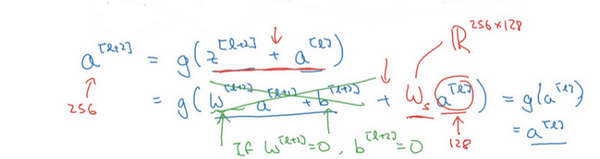
除此之外,关于残差网络,另一个值得探讨的细节是,假设 z\^{\\left\\lbrack l + 2\\right\\rbrack}\\(与\\)a^{\[l\]}具有相同维度,所以**ResNets**使用了许多**same**卷积,所以这个a^的维度等于这个输出层的维度。之所以能实现跳跃连接是因为same卷积保留了维度,所以很容易得出这个捷径连接,并输出这两个相同维度的向量。
如果输入和输出有不同维度,比如输入的维度是128, a\^{\\left\\lbrack l + 2\\right\\rbrack}\\(的维度是256,再增加一个矩阵,这里标记为\\)W_{s}\\(,\\)W_{s}\\(是一个256×128维度的矩阵,所以\\)W_{s}a\^{\\left\\lbrack l\\right\\rbrack}\\(的维度是256,这个新增项是256维度的向量。不需要对\\)W_{s}\\(做任何操作,它是网络通过学习得到的矩阵或参数,它是一个固定矩阵,\*\*padding\*\*值为0,用0填充\\)a\^{\[l\]},其维度为256,所以者几个表达式都可以。
最后,来看看ResNets 的图片识别。这些图片是从何凯明等人论文中截取的,这是一个普通网络,给它输入一张图片,它有多个卷积层,最后输出了一个Softmax。

如何把它转化为ResNets 呢?只需要添加跳跃连接。这里只讨论几个细节,这个网络有很多层3×3卷积,而且它们大多都是same 卷积,这就是添加等维特征向量的原因。所以这些都是卷积层,而不是全连接层,因为它们是same卷积,维度得以保留,这也解释了添加项 z\^{\\left\\lbrack l + 2 \\right\\rbrack} + a\^{\\left\\lbrack l\\right\\rbrack}(维度相同所以能够相加)。
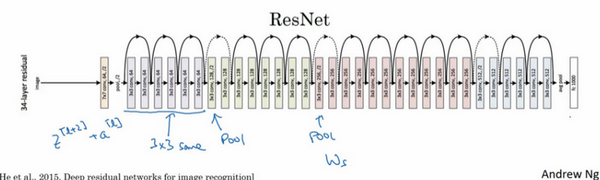
ResNets 类似于其它很多网络,也会有很多卷积层,其中偶尔会有池化层或类池化层的层。不论这些层是什么类型,都需要调整矩阵\(W_{s}\)的维度。普通网络和ResNets 网络常用的结构是:卷积层-卷积层-卷积层-池化层-卷积层-卷积层-卷积层-池化层......依此重复。直到最后,有一个通过softmax进行预测的全连接层。