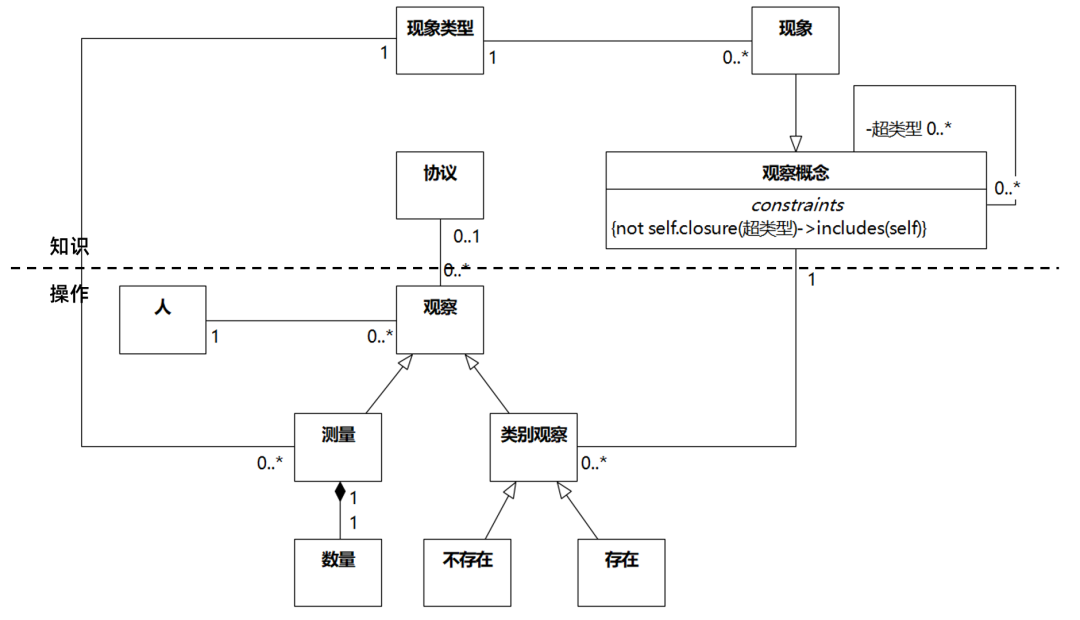
"Analysis Patterns"的第3章的图3.10,原图如下:
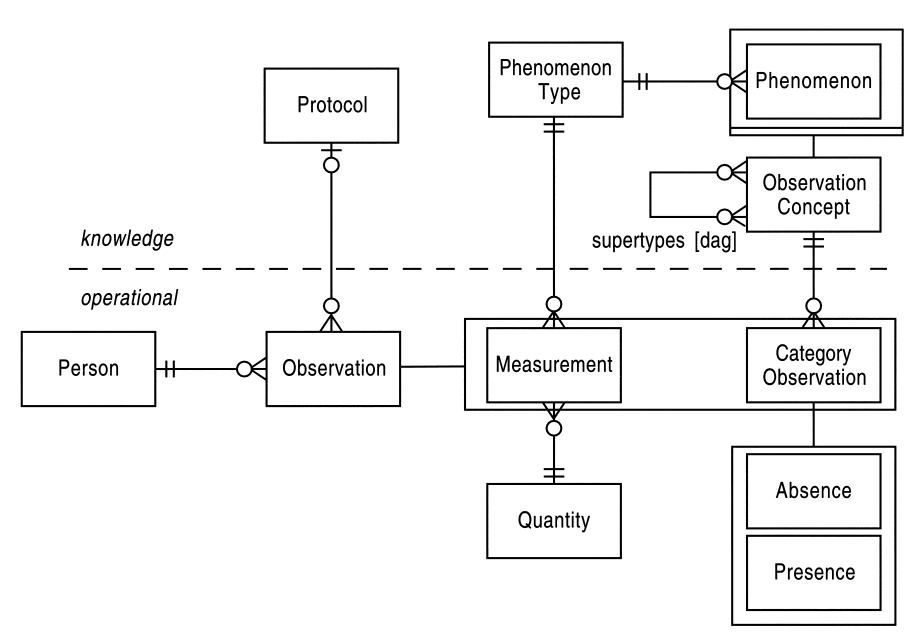
2004和2020中译本都只是翻译了文字,在2024中译本中,我们先照猫画虎用UML改编如下:
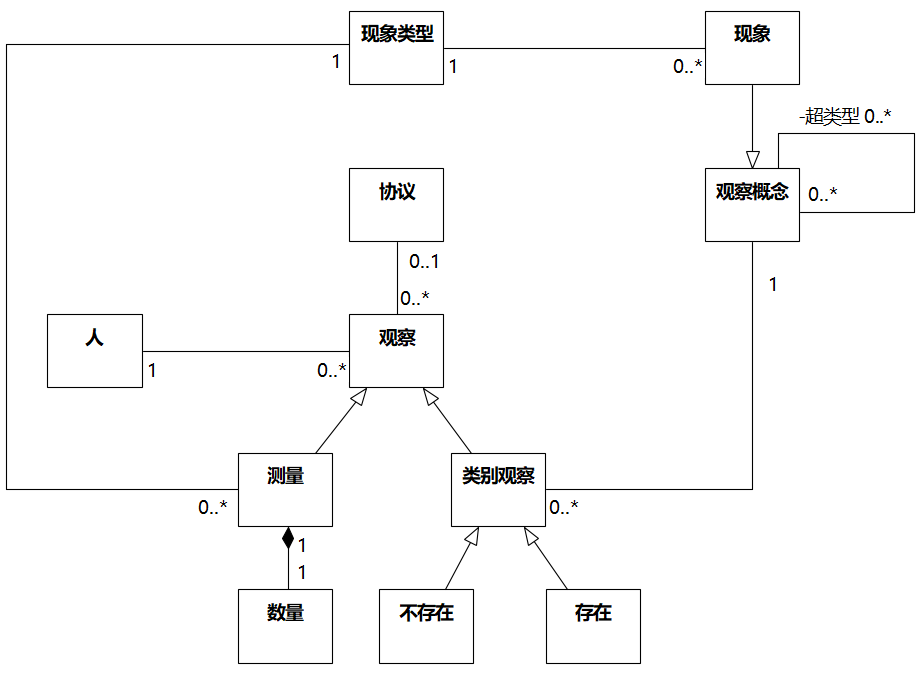
但还有一个问题没有解决,在"观察概念"的自反关联中,Fowler标了一个[dag]:

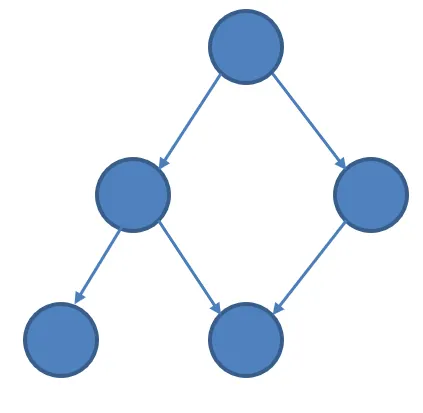
DAG即有向无环图(Directed Acyclic Graph),意思是"观察概念"自反关联组成的对象图应该是一个有向无环图,像下面这样:
这个约束是为了防止出现某个实例的超类型直接或间接地又把该实例作为超类型。
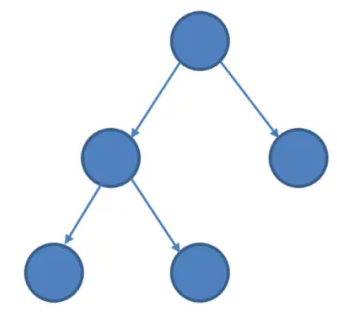
之所以是有向无环图,是因为"超类型"一端的多重性可以为"多",如果最多为1,那就是一棵有向树,例如:
虽然Fowler在附录中有说明,[dag]是类别图的一个约束标记,但这样表示是不严谨的。
之前漫谈文章中评点过图3.5,图上也放了一个标记[bag]:
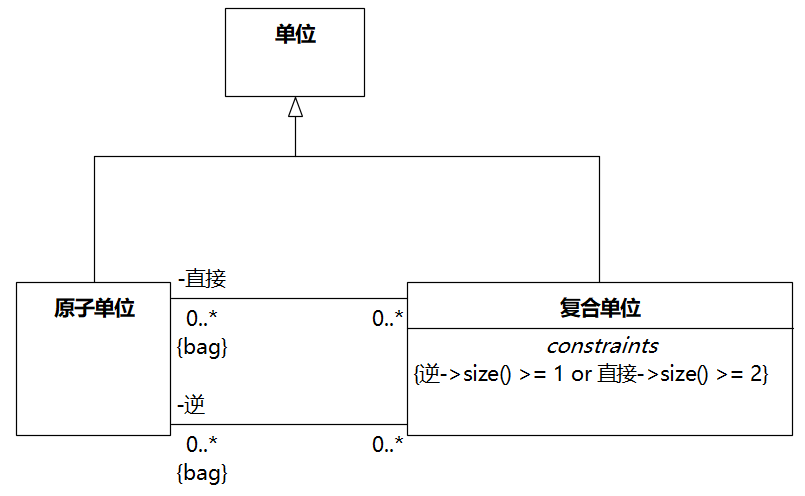
这是可以的,因为它约束的是某个"复合单位"链接到的"原子单位"集合(无序、可重复)。
而本文开头图3.10中的[dag]并不是对某个"观察概念"的"超类型"集合的约束,而是描述存在图中所定义自反关联的所有"观察概念"以及它们之间的链接所形成的图,在"超类型"那里简单这样标一下是不合适的。
如果想更严谨地表达这个约束,可以用OCL,如下:
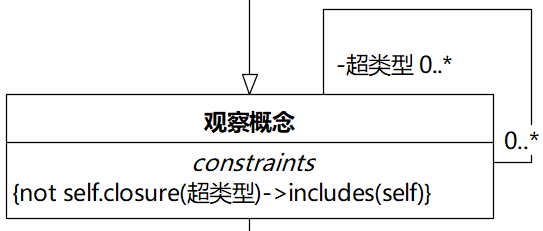
意思是,对于任何一个"观察概念",不允许出现这样的情况:求它的"超类型"闭包所得的"观察概念"集合中包含它自己。
最后得到的图3.10如下: