
上一篇:《搞清楚这个老六的真面目!逐层'剥开'人工智能中的卷积神经网络(CNN)》
序言:现在让我们开始走进卷积神经网络(CNN)的世界里。和传统编程完全不同,在人工智能的程序代码里,您看不到明确的算法规则,看到的只是神经网络的配置说明。这里的代码不会像传统编程那样去具体实现每个功能。比如说,如果您想让电脑分辨猫和狗,您不需要写代码去解释猫和狗长得什么样,而是通过描述神经网络的配置,让它在训练过程中通过数据自己学会。描述就像艺术,如何恰到好处地增添一笔,才能带来非凡的效果?这正是设计人工智能的精髓!!
(点一点关注,避免未来更新无法及时通知您)
在前面的知识中,我们创建了一个能够识别时装图像的神经网络。为了方便,这里是完整的代码:
import tensorflow as tf
data = tf.keras.datasets.fashion_mnist
(training_images, training_labels), (test_images, test_labels) = data.load_data()
training_images = training_images / 255.0
test_images = test_images / 255.0
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(input_shape=(28, 28)),
tf.keras.layers.Dense(128, activation=tf.nn.relu),
tf.keras.layers.Dense(10, activation=tf.nn.softmax)
])
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model.fit(training_images, training_labels, epochs=5)
要将其转换为卷积神经网络,我们只需在模型定义中使用卷积层。同时,我们还会添加池化层。
要实现一个卷积层,您将使用 tf.keras.layers.Conv2D 类型。它接受一些参数,比如层中要使用的卷积数量、卷积的大小、激活函数等。
例如,下面是一个作为神经网络输入层的卷积层:
tf.keras.layers.Conv2D(64, (3, 3), activation='relu',
input_shape=(28, 28, 1)),
在这里,我们希望这一层学习到 64 个卷积。它会随机初始化这些卷积,并随着时间推移,学习出最适合将输入值与其标签匹配的滤波器值。(3, 3) 表示滤波器的大小。之前我展示过 3 × 3 的例子。
在这里,我们指定滤波器大小为 3 × 3,这也是最常见的滤波器大小;您可以根据需要更改,但通常会看到像 5 × 5 或 7 × 7 这样的奇数轴,因为滤波器会从图像边缘去除像素,稍后您会看到具体效果。
activation 和 input_shape 参数与之前相同。因为我们在这个示例中使用的是 Fashion MNIST,所以形状仍然是 28 × 28。不过要注意,因为 Conv2D 层是为多色图像设计的,所以我们将第三维指定为 1,因此输入形状是 28 × 28 × 1。彩色图像的第三参数通常是 3,因为它们以 R、G、B 三个通道的值存储。
接下来是在神经网络中使用池化层的方法。通常您会在卷积层之后立即使用它:
tf.keras.layers.MaxPooling2D(2, 2),
在图 3-4 的示例中,我们将图像分成 2 × 2 的小块,并在每个小块中选取最大值。这个操作可以参数化,以定义池的大小。这里的 (2, 2) 表示我们的池大小为 2 × 2。
现在,让我们来看看使用 CNN 处理 Fashion MNIST 的完整代码:
import tensorflow as tf
data = tf.keras.datasets.fashion_mnist
(training_images, training_labels), (test_images, test_labels) = data.load_data()
training_images = training_images.reshape(60000, 28, 28, 1)
training_images = training_images / 255.0
test_images = test_images.reshape(10000, 28, 28, 1)
test_images = test_images / 255.0
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(64, (3, 3), activation='relu',
input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(2, 2),
tf.keras.layers.Conv2D(64, (3, 3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation=tf.nn.relu),
tf.keras.layers.Dense(10, activation=tf.nn.softmax)
])
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model.fit(training_images, training_labels, epochs=50)
model.evaluate(test_images, test_labels)
classifications = model.predict(test_images)
print(classifications[0])
print(test_labels[0])
这里有一些需要注意的地方。还记得之前我说过输入图像的形状必须与 Conv2D 层的预期相匹配吗?我们将其更新为 28 × 28 × 1 的图像吗?数据也需要相应地重塑。28 × 28 表示图像的像素数量,而 1 表示颜色通道的数量。对于灰度图像,通常为 1;对于彩色图像,则为 3,因为它有三个通道(红色、绿色和蓝色),数字表示该颜色的强度。
因此,在对图像进行归一化之前,我们还需要将每个数组重塑为带有额外维度的形状。以下代码将我们的训练数据集从 60,000 张每张 28 × 28 的图像(因此是一个 60,000 × 28 × 28 的数组)更改为 60,000 张每张 28 × 28 × 1 的图像:
training_images = training_images.reshape(60000, 28, 28, 1)
然后我们对测试数据集执行相同的操作。
还要注意,在最初的深度神经网络(DNN)中,我们在将输入传递到第一个 Dense 层之前使用了一个 Flatten 层。而这里的输入层中,我们省略了这一层,只需指定输入形状。注意,在经过卷积和池化后,在进入 Dense 层之前,数据将被展平。
将该网络在相同的数据上训练 50 个周期,与第 2 章中展示的网络相比,我们可以看到准确率有显著提升。之前的例子在 50 个周期后在测试集上达到了 89% 的准确率,而这个网络在大约一半的周期(24 或 25 个)就能达到 99%。所以我们可以看到,添加卷积层确实提高了神经网络的图像分类能力。接下来让我们看看图像在网络中的传递过程,以更深入理解其工作原理。
探索卷积网络
您可以使用 model.summary 命令检查您的模型。当您在我们一直在处理的 Fashion MNIST 卷积网络上运行它时,您会看到类似这样的结果:
Model: "sequential"
Layer (type) Output Shape Param #
=================================================================
conv2d (Conv2D) (None, 26, 26, 64) 640
max_pooling2d (MaxPooling2D) (None, 13, 13, 64) 0
conv2d_1 (Conv2D) (None, 11, 11, 64) 36928
max_pooling2d_1 (MaxPooling2 (None, 5, 5, 64) 0
flatten (Flatten) (None, 1600) 0
dense (Dense) (None, 128) 204928
dense_1 (Dense) (None, 10) 1290
=================================================================
Total params: 243,786
Trainable params: 243,786
Non-trainable params: 0
我们先来看一下"输出形状"列,以了解这里发生了什么。我们的第一层会处理 28 × 28 的图像,并应用 64 个滤波器。但是,由于滤波器是 3 × 3 的,图像周围会丢失 1 像素的边框,从而将整体信息减少到 26 × 26 像素。参考图 3-6,如果我们将每个方框看作图像中的一个像素,第一个可能的滤波操作会从第二行、第二列开始。右侧和底部也会出现相同的情况。
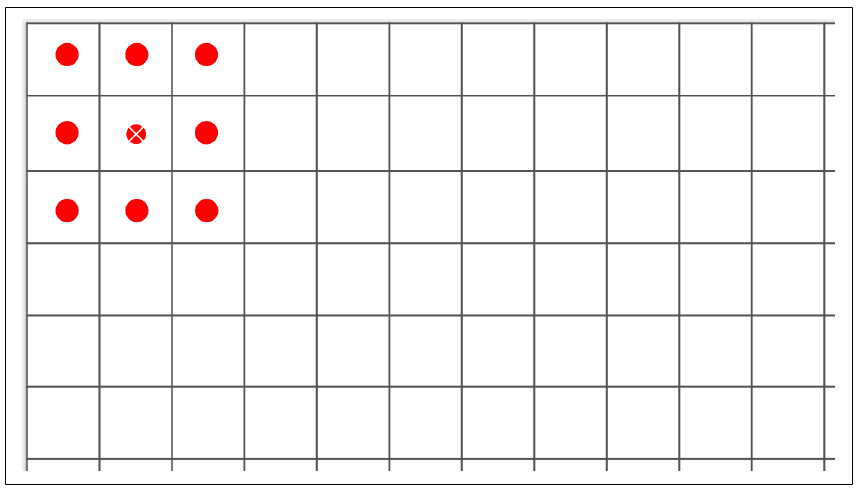
图 3-6:运行滤波器时丢失像素因此,一个 A × B 像素大小的图像在经过 3 × 3 滤波器后会变成 (A--2) × (B--2) 像素。同样地,5 × 5 的滤波器会将其变成 (A--4) × (B--4),依此类推。由于我们使用的是 28 × 28 的图像和 3 × 3 的滤波器,所以我们的输出现在是 26 × 26。
接下来,池化层是 2 × 2 的,因此图像在每个轴上会缩小一半,变成 (13 × 13)。下一个卷积层会进一步缩小到 11 × 11,而下一个池化层再进行四舍五入后,会将图像缩小到 5 × 5。
这样一来,当图像经过两层卷积后,结果将会是多个 5 × 5 的小图像。那么会有多少个呢?我们可以在参数数列(Param #)中看到。
每个卷积是一个 3 × 3 的滤波器,加上一个偏置。还记得之前在密集层中,公式是 Y = mX + c 吗?其中 m 是我们的参数(即权重),c 是偏置。这里的原理类似,只不过滤波器是 3 × 3 的,因此需要学习 9 个参数。因为我们定义了 64 个卷积,总共有 640 个参数(每个卷积有 9 个参数加一个偏置,总共 10 个,然后有 64 个卷积)。
MaxPooling 层并不会学习任何内容,它只是缩小图像的尺寸,因此没有学习参数,所以显示为 0。
接下来的卷积层有 64 个滤波器,但每一个滤波器都会跨前一个 64 个滤波器进行相乘,每个滤波器有 9 个参数。我们为新的 64 个滤波器中的每一个都增加一个偏置,因此参数总数应为 (64 × (64 × 9)) + 64,得出 36,928 个需要网络学习的参数。
如果这里有些复杂,您可以尝试将第一层的卷积数量改为一个不同的值,比如 10。您会发现第二层的参数数量变为 5,824,即 (64 × (10 × 9)) + 64。
当我们完成第二次卷积时,图像变为 5 × 5,且我们有 64 个这样的图像。将这些相乘后,我们得到 1,600 个值,这些值会传入一个包含 128 个神经元的密集层。每个神经元有一个权重和一个偏置,总共 128 个神经元,因此网络要学习的参数数量是 ((5 × 5 × 64) × 128) + 128,得出 204,928 个参数。
最后一层密集层有 10 个神经元,接受前一个 128 个神经元的输出,因此学习的参数数量为 (128 × 10) + 10,即 1,290。
总参数数量就是这些的总和:243,786。
训练这个网络需要我们学习这 243,786 个参数的最佳组合,以便将输入图像与标签匹配。由于参数更多,训练过程会更慢,但从结果可以看到,它也构建了更准确的模型!
当然,在这个数据集中我们仍然受限于图像是 28 × 28、单色且居中的。接下来我们将使用卷积来探索更复杂的数据集,其中包含马和人的彩色图像,我们会尝试判断图像中是马还是人。在这种情况下,主体不一定会像 Fashion MNIST 那样居中,所以我们必须依赖卷积来捕捉辨别特征。
本篇我们自己动手描述了一个卷积神经网络,下一篇,我们就用这个CNN神经网络去分辨出人类与动物(马)。