蚁群算法（Ant Colony Optimization）详细解读

蚁群算法（Ant Colony Optimization, ACO）是一种基于自然界中蚂蚁觅食行为的优化算法，主要用于解决组合优化问题，特别是旅行商问题（TSP）等路径优化问题。算法通过模拟蚂蚁释放和跟随信息素（Pheromone）的行为，实现多个解的迭代优化，具有强大的全局搜索能力。

1. 算法思想

在自然界中，蚂蚁通过释放信息素来标记行走的路径，其他蚂蚁倾向于选择信息素浓度更高的路径。随着时间的推移，信息素浓度高的路径会吸引更多的蚂蚁，使得蚂蚁逐渐趋向于较短的路径。蚁群算法模拟这种信息素机制，用于寻优问题。

2. 核心概念

蚂蚁（Ant）：在算法中，每只蚂蚁代表一个解。算法会在每轮迭代中派遣多个蚂蚁寻找路径，每只蚂蚁基于信息素和启发函数选择下一步。
信息素（Pheromone）：每条路径上会有一定浓度的信息素，表示蚂蚁对路径的偏好。路径上信息素越多，蚂蚁选择该路径的概率越大。
启发式信息（Heuristic Information）：为加强局部选择性，算法中通常引入距离、成本等启发信息，帮助蚂蚁判断路径的吸引力。
信息素更新（Pheromone Update）：每轮迭代结束后，算法会根据路径质量更新信息素，优秀路径的信息素增加，较差路径的信息素则因挥发而减少。

3. 蚁群算法的步骤

初始化

初始化参数：设定信息素浓度、蚂蚁数量、信息素挥发系数等参数。
初始化信息素矩阵：通常初始化所有路径的初始信息素浓度为相同值。

迭代过程

每一轮迭代中，算法执行以下步骤：

路径选择：每只蚂蚁从一个起点开始，根据信息素浓度和启发式信息选择下一节点，构建完整的解。
- 路径选择的概率计算公式通常为：

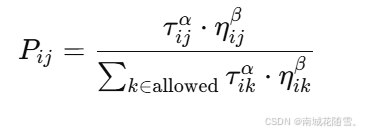
- 其中：
  - τij 表示路径 i 到 j 的信息素浓度；
  - ηij 是启发式信息（如距离的倒数）；
  - α 和 β 是调整信息素和启发式信息重要性的参数。
路径评估：所有蚂蚁构建完解后，评估每条路径的质量（如路径总长度、路径花费等）。
信息素更新：
- 信息素挥发：对所有路径信息素进行衰减，防止信息素无限增加导致过早收敛。

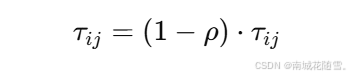
其中，ρ 是信息素挥发率。
信息素增加：对本轮迭代中的优秀路径增加信息素，通常使用每条路径的总花费倒数表示贡献

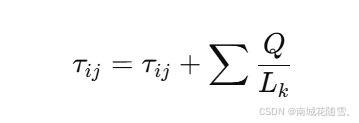
- 其中 L 是路径的长度，Q 是信息素增强常数。
迭代：重复上述过程，直到满足终止条件（如达到最大迭代次数或找到满足条件的解）。

4. 参数设置

信息素重要性参数 α：影响蚂蚁对信息素的依赖程度。值越大，蚂蚁对信息素的依赖越强。
启发信息重要性参数 β：影响蚂蚁对启发信息（如距离）的依赖程度。值越大，蚂蚁更倾向于选择近距离的节点。
信息素挥发系数 ρ：控制信息素的衰减速率，值越小保留的信息素越多，影响路径的多样性。
信息素增强常数 Q：决定信息素增加量，通常根据问题的规模和路径的质量设置。

5. Java 实现示例（旅行商问题）

以下代码示例展示了蚁群算法解决旅行商问题的核心逻辑：

java 复制代码

import java.util.Random;

public class AntColonyTSP {
    private static final int CITIES = 5;
    private static final int ANTS = 10;
    private static final int MAX_ITERATIONS = 1000;
    private static final double ALPHA = 1.0; // 信息素重要性
    private static final double BETA = 5.0;  // 启发信息重要性
    private static final double EVAPORATION = 0.5; // 信息素挥发率
    private static final double Q = 100;     // 信息素增强常数

    private double[][] distances;
    private double[][] pheromones;

    private Random random = new Random();

    public AntColonyTSP(double[][] distances) {
        this.distances = distances;
        this.pheromones = new double[CITIES][CITIES];

        // 初始化信息素矩阵
        for (int i = 0; i < CITIES; i++) {
            for (int j = 0; j < CITIES; j++) {
                pheromones[i][j] = 1.0;
            }
        }
    }

    public void solve() {
        int[] bestTour = null;
        double bestTourLength = Double.MAX_VALUE;

        for (int iteration = 0; iteration < MAX_ITERATIONS; iteration++) {
            int[][] tours = new int[ANTS][CITIES];
            double[] tourLengths = new double[ANTS];

            // 每只蚂蚁生成一条路径
            for (int ant = 0; ant < ANTS; ant++) {
                tours[ant] = constructTour();
                tourLengths[ant] = calculateTourLength(tours[ant]);
                
                // 更新最佳路径
                if (tourLengths[ant] < bestTourLength) {
                    bestTourLength = tourLengths[ant];
                    bestTour = tours[ant];
                }
            }

            // 更新信息素
            evaporatePheromones();
            for (int ant = 0; ant < ANTS; ant++) {
                depositPheromones(tours[ant], tourLengths[ant]);
            }
        }

        // 输出最优解
        System.out.println("Best tour length: " + bestTourLength);
        System.out.print("Best tour: ");
        for (int city : bestTour) {
            System.out.print(city + " ");
        }
        System.out.println();
    }

    private int[] constructTour() {
        boolean[] visited = new boolean[CITIES];
        int[] tour = new int[CITIES];
        int currentCity = random.nextInt(CITIES);

        tour[0] = currentCity;
        visited[currentCity] = true;

        for (int i = 1; i < CITIES; i++) {
            int nextCity = selectNextCity(currentCity, visited);
            tour[i] = nextCity;
            visited[nextCity] = true;
            currentCity = nextCity;
        }

        return tour;
    }

    private int selectNextCity(int currentCity, boolean[] visited) {
        double[] probabilities = new double[CITIES];
        double sum = 0.0;

        for (int city = 0; city < CITIES; city++) {
            if (!visited[city]) {
                probabilities[city] = Math.pow(pheromones[currentCity][city], ALPHA) *
                                      Math.pow(1.0 / distances[currentCity][city], BETA);
                sum += probabilities[city];
            } else {
                probabilities[city] = 0.0;
            }
        }

        double rand = random.nextDouble() * sum;
        for (int city = 0; city < CITIES; city++) {
            if (!visited[city]) {
                rand -= probabilities[city];
                if (rand <= 0.0) {
                    return city;
                }
            }
        }
        return -1;
    }

    private double calculateTourLength(int[] tour) {
        double length = 0.0;
        for (int i = 0; i < CITIES - 1; i++) {
            length += distances[tour[i]][tour[i + 1]];
        }
        length += distances[tour[CITIES - 1]][tour[0]];
        return length;
    }

    private void evaporatePheromones() {
        for (int i = 0; i < CITIES; i++) {
            for (int j = 0; j < CITIES; j++) {
                pheromones[i][j] *= (1 - EVAPORATION);
            }
        }
    }

    private void depositPheromones(int[] tour, double tourLength) {
        double pheromoneToDeposit = Q / tourLength;
        for (int i = 0; i < CITIES - 1; i++) {
            pheromones[tour[i]][tour[i + 1]] += pheromoneToDeposit;
            pheromones[tour[i + 1]][tour[i]] += pheromoneToDeposit;
        }
        pheromones[tour[CITIES - 1]][tour[0]] += pheromoneToDeposit;
        pheromones[tour[0]][tour[CITIES - 1]] += pheromoneToDeposit;
    }

    public static void main(String[] args) {
        double[][] distances = {
            {0, 2, 2, 5, 7},
            {2, 0, 4, 8, 2},
            {2, 4, 0, 1, 3},
            {5, 8, 1, 0, 2},
            {7, 2, 3, 2, 0}
        };
        AntColonyTSP tsp = new AntColonyTSP(distances);
        tsp.solve();
    }
}

6. 蚁群算法的优缺点

优点

全局搜索能力强：通过信息素累积和随机选择，使得蚁群算法具有较强的全局搜索能力。
动态适应性：路径上的信息素会逐渐调整，使算法在搜索过程中动态适应局部环境。

缺点

参数敏感：信息素衰减率、信息素和启发信息权重等参数选择对算法效果影响大。
收敛速度：可能收敛较慢，尤其在早期迭代中探索较多，适用于解决规模适中的问题。

7. 应用

蚁群算法适用于多种组合优化问题，尤其是在路径规划、调度、网络路由等方面。