多校A层冲刺NOIP2024模拟赛18
T1 选彩笔(rgb)
签到题,但是没签上。。。
没想到三维前缀和,直接上了个bitset。
就是直接二分答案,然后枚举这三维每维的区间的起点,前缀和查数量是否 大于等于 K 即可,也可以把二分答案改为第一维的双指针,少一个 log 。
T2 兵蚁排序(sort)
比T1还签到,但是没写 freopen 挂 100。
从 b 数组里挨个去在 a 数组里匹配,然后 O(n) 拉过来就行。
T3 人口局 DBA(dba)
数学推式子。
但是有很多部分分的数位DP,骗了 97 分。
简单来说就是解一个方程满足 x_1 + x_2 + x_3 + ······ + x_{n-1} + x_{n} = sum , x1 \\lt p , \\forall \\ \\ i ∈ \[1,n\] \\ \\ 0 \\le x_i \\lt m 的解的个数。
首先不考虑 x1 \\lt p 的限制,然后你就可以容斥,钦定有 k 个 x 是 大于 m 的,把他们斥掉,然后就有一个式子(直接插板):
\[f_{a,s} \sum_{k=0}^{a} (-1)^k \binom{a}{k} \binom{s-km+a-1}{a-1} \]
如果考虑上 x1 \\lt p 的限制,那就可以直接枚举 x1 ,所以有:
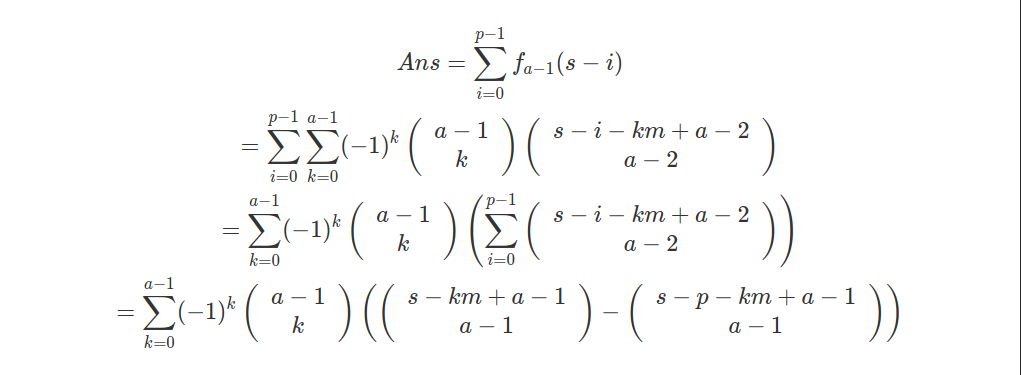
那个后面求和式的化简就是因为 组合数的下面那个不变,所以在杨辉三角上就是竖着的一列
如图:
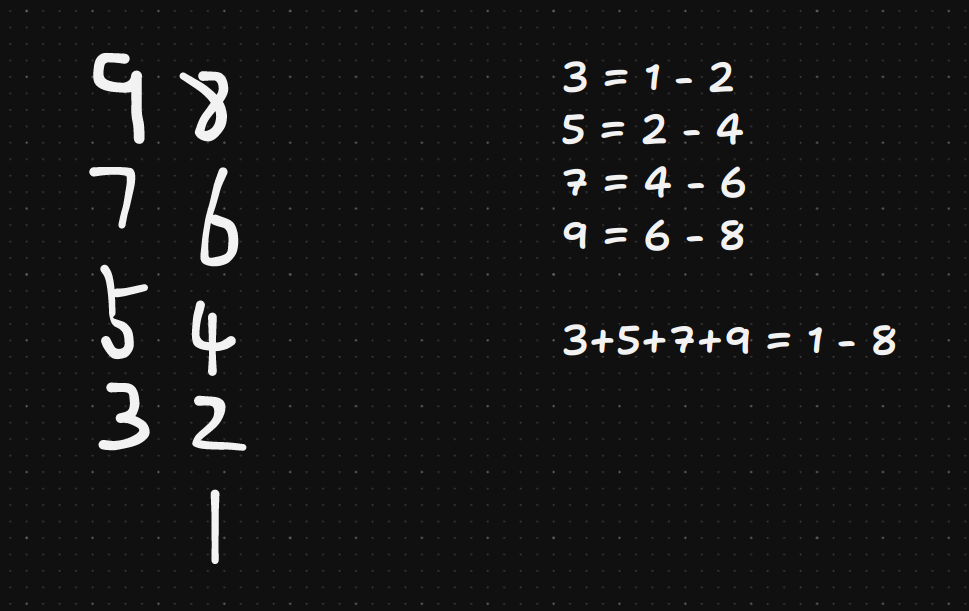
T4 银行的源起(banking)
因为讲过了,所以这篇讲的简单点。 算了,还是稍微详细点吧。
首先考虑只有一个银行的时候怎么求,那肯定是所有人都往一个银行跑,所以枚举点然后算贡献?
其实这种题有 O (n) 做法。
首先以 1 为根,我们直接考虑每条边的贡献,对于一条边,他的权值是 w ,连接着点 j 和他的父亲 fa_j 。

对于这条边,要么是 j 和他的子树里面的点往上走经过这条边,要么是上面的点下来,这时候我们设 sz_j 是 j 及其子树里面的点的权值之和, tot 表示整棵树的权值和,直接取 w \\times \\min( sz_j , tot - sz_j) , 作为这条边的贡献即可。
为什么对,来证明一下:
上面的式子只能保证对于一条边来说是最优的,但是不能保证全局都是这样的,但其实全局最优可以被证明只有在每个都最优的时候才成立。

证毕。此时我们得到了 O(n) 解决一个银行的问题的方法。那如果有两个银行呢,这个时候也一定存在一条边没有人走,所以我们枚举一条边并把它断开,然后对于两棵树分别求贡献加和,即可 O(n\^2) 解决。
O(n\^2) 解决不了,那就看看能不能上数据结构优化。
优化肯定要从贡献方面入手,那就再看看那个贡献的式子, ans_j = w_j \\times \\min( sz_j , tot - sz_j ) ,这个 min 就很难直接优化,那就分讨, 如果 sz_j \\le \\frac{tot}{2} , ans_j = w_j \\times sz_j ,否则 ans_j = w_j \\times (tot - sz_j ) ,那么这东西可以上值域线段树,具体来说,对于 sz 开一颗值域线段树,然后维护好 \\sum w_j 、 \\sum w_j \\times sz_j 然后就可以做了。
主体思路有了,具体的分析一下:
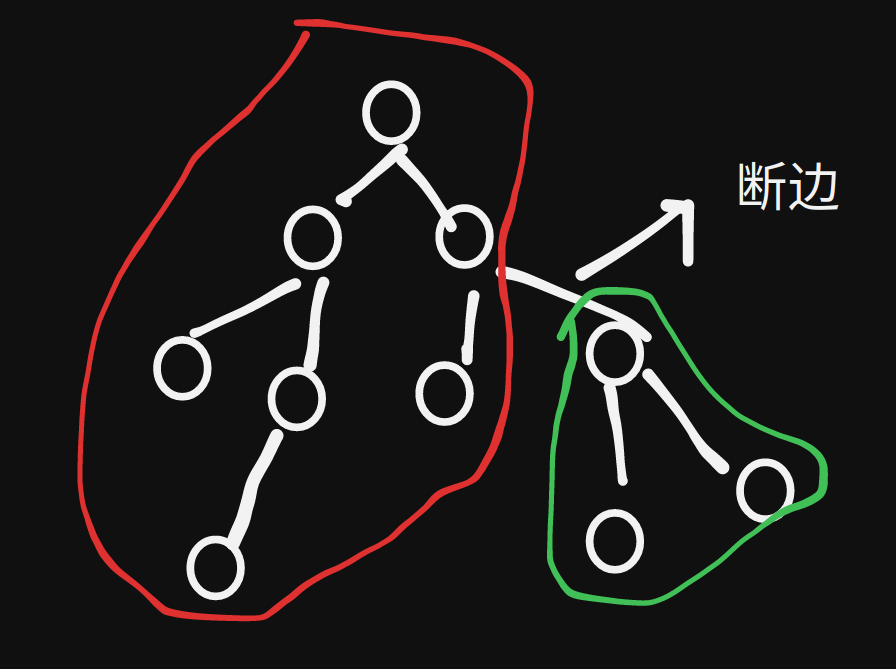
在这个图里面,我们将这棵树分成了两部分,一颗红的,一颗绿的,我们分别求贡献。
对于绿色的部分很好求,就用刚才的至于线段树就行,dfs时线段树合并 n( log (n) ) ,对于红色的部分稍微麻烦一点。
首先考虑红色的部分相对于原树有哪些变化:
红树的 tot = sz_1 - sz_j
对于绿树中的根 j ,从他的父亲 x 到 1 的这条链上面的点 i , sz_i 都减少了 sz_j 。
首先链上的点的贡献肯定得单求,可以维护一颗树状数组,然后每次查询时先链减 ,然后问,但是一个技巧可以不用链减,现在的分讨条件是 sz_i - sz_j \\le \\frac{tot}{2} ,那么直接移项,分讨条件变为 sz_i \\le \\frac{tot}{2} + sz_j ,同时最后求的答案要用 减去 sz_j 之后的值。(写出式子来就会了)
接下来就是红树中除了链上的部分了,我们发现这部分很难直接求,线段树也不好维护,但是他就是全局除了链上和绿树上以外的所有点,所以我们求出全局对于 \\frac{tot}{2} 的贡献,这部分可以弄一颗静态的全局线段树,也可以直接离散化后前缀和 ,然后减去 链上以及绿树中对于 \\frac{tot}{2} 的贡献即可,这部分都可以用刚才维护的东西直接求。
那我们就求完了,这道题主要是多注意注意细节就行了。