本文是对公开论文的核心提炼，旨在进行学术交流。如有任何侵权问题，请及时联系号主以便删除。

来源：晓飞的算法工程笔记公众号，转载请注明出处

论文: Open-RAG: Enhanced Retrieval-Augmented Reasoning with Open-Source Large Language Models

论文地址：https://arxiv.org/abs/2410.01782
论文代码：https://openragmoe.github.io

创新性

\({\tt Open-RAG}\) 具备以下特点：

将任意稠密的LLM转变为参数高效的稀疏专家混合（sparse mixture of experts，MoE）模型，能够处理复杂的推理任务，包括单步和多步查询。
特别地训练模型应对看似相关但实际上具有误导性的挑战性干扰，同时仅在适配器中扩展MoE，保持模型的规模。
通过结合结构学习、架构转换和基于反思的生成，利用潜在嵌入学习动态选择相关专家并有效整合外部知识，以实现更准确和上下文支持的响应生成及其有效性的估计。
通过一种混合自适应检索方法，以确定检索的必要性，并在性能提升与推理速度之间取得平衡。

内容概述

检索增强生成（Retrieval-Augmented Generation，RAG）能够提高大型语言模型（Large Language Models，LLMs）的准确性，但现有方法往往在有效利用检索证据方面表现出有限的推理能力，尤其是在使用开源LLMs时。

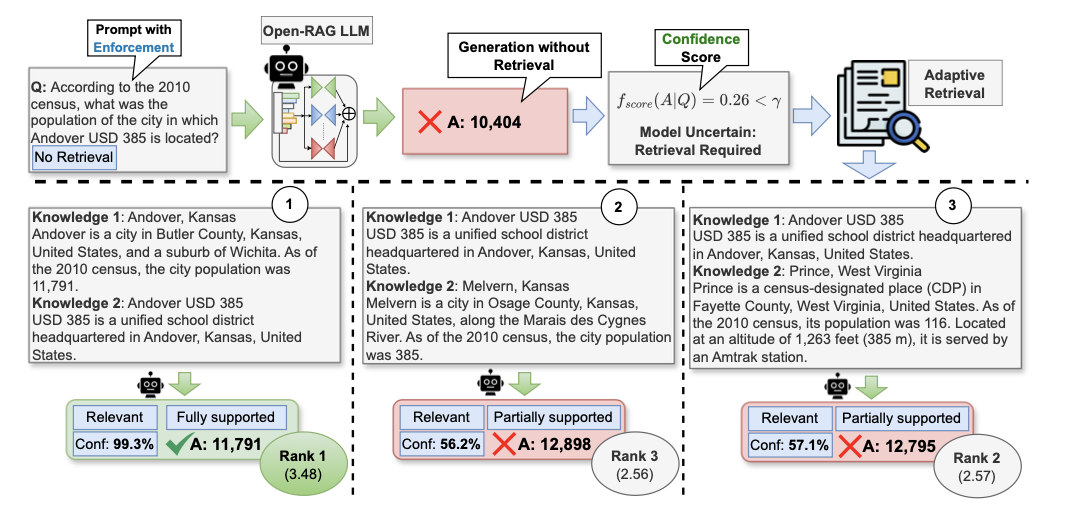
论文提出 \({\tt Open-RAG}\) ，旨在增强开源LLMs中RAG的推理能力。为了控制开源LLMs的行为，生成更具上下文支持的响应，采用来自Self-RAG的基于反思的生成方法，用四种特殊的反思标记类型增强输出词汇（对应上图中的蓝色部分）：检索（Retrieval）、相关性（Relevance）、基础（Grounding）和实用（Utility）。

将 \({\tt Open-RAG}\) LLM 定义为一个模型 \(\mathcal{M}_{G}\) ，该模型在给定输入查询 \(q\) 的情况下，目标生成一个包含 \(m\) 个标记的输出序列 \(o = [o_1, o_2, ..., o_m]\) ，其处理过程如下：

在训练过程中，模型学习生成指示是否需要检索以回答 \(q\) 的检索标记（[RT]/[NoRT]）。在推理过程中，则采用混合自适应检索方案，综合检索标记和模型置信度判断是否需要检索。
如果不需要检索， \(\mathcal{M}{G}\) 仅使用LLM的参数知识生成响应（即将 \(o\) 作为 \(y{pred}\) 返回）。
如果需要检索，对于来自外部知识源 \(D = \{d_i\}{i=1}^{N_d}\) 的单步或多步，使用用户定义的冻结检索器 \(R\) 来检索前 \(k\) 个文档 \(S = \{s_t\}{t=1}^{k}\) ，其中每个 \(s_t\) 由 \(\{r_j\}_{j=1}^{N_H}\) 组成， \(r_j \in D\) ， \(N_H\) 表示步数。
- 对于每个检索到的内容 \(s_t\) ， \(\mathcal{M}_{G}\) 生成一个相关性标记、输出响应 \(y_t\) 、一个基础标记和一个实用标记。
  - 相关性标记（[Relevant/Irrelevant]）指示 \(s_t\) 是否与 \(q\) 相关。
  - 基础标记（[Fully Supported/Partially Supported/No Support]）指示 \(y_t\) 是否得到 \(s_t\) 的支持。
  - 实用标记（[U:1]-[U:5]）定义 \(y_t\) 对 \(q\) 的有用程度。
- 并行处理每个 \(s_t\) 并通过对它们（即所有 \(y_t\) ）进行排名来生成最终答案 \(y_{pred}\) ，排名依据是对应预测的相关性、基础和实用标记的归一化置信度的加权和。

Open-RAG

数据收集

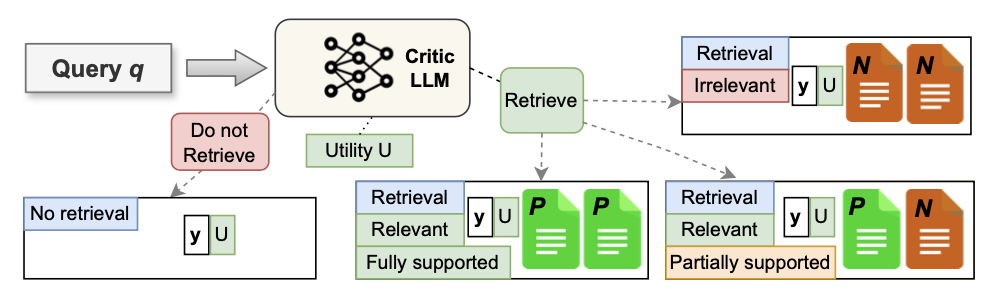
为了使 \({\tt Open-RAG}\) 能够处理无检索查询，以及需要检索的单步和多步查询，使用各种类型的任务和数据集构建训练数据。给定原始数据集中的输入输出数据对 ( \(q\) , \(y\) )，通过利用真实标签注释或LLM \(C\) 生成标记来增强数据，从而创建监督数据。

如果 \(C\) 添加的相应检索标记是 [RT]，则会进一步增强数据，根据以下方式创建三种不同的新标记。

使用 \(R\) 检索前 \(k\) 个文档 \(S\) 。对于每个检索到的文档 \(s_t\) ， \(C\) 评估 \(s_t\) 是否相关，并返回相关性标记。为了解决单步和多步查询的问题，为数据管道配备了一个步数统一启发式：如果至少有一个段落 \(\{r_j\} \in s_t\) 是相关的，则将相关性标记添加为 [Relevant]，否则使用 [Irrelevant]。
当预测为 [Relevant] 时，为了使 \(\mathcal{M}_{G}\) 能够在 \(s_t\) 中更细致地区分有用和干扰上下文，设计了一个数据对比启发式：（i）对于单步RAG数据集，直接使用 \(C\) 来标记基础标记；（ii）对于多步RAG数据集，如果所有段落 \(\{r_j\} \in s_t\) 被单独预测为 [RT]，那么将 [Fully Supported] 添加为基础标记；否则，使用 [Partially Supported]。
无论相关性标记的预测如何，都使用 \(C\) 为 \(y\) 提供相对于 \(q\) 的实用分数。

参数高效的`MoE`微调

RAG任务本质上是复杂的，由单一（单步）或多个（多步）段落的查询等各种组件组成。根据这些复杂性选择性地利用模型的不同部分，可以促进对多样化输入上下文的更自适应和更细致的推理能力。

因此，论文采用稀疏升级（sparse upcycling）将 \(\mathcal{M}_{G}\) 转换为MoE架构，并根据需要动态学习为每个具有多样化复杂性的查询（例如，单步/多步）选择性激活最合适的专家。这种选择性激活是通过前面量身定制的训练数据进行学习（微调）的，确保模型能够区分有用信息和误导信息。

稀疏MoE \({\tt Open-RAG}\) 模型通过一个参数高效的MoE转换块增强了密集主干LLM的FFN层，该转换块由一组专家层 \(\mathbf{E} = \{\mathcal{E}e\}{e=1}^{N_E}\) 以及有效的路由机制组成。

每个专家层包含一个复制的原始共享FFN层权重，通过具有参数 \(\theta_e\) 的适配器模块 \(\mathcal{A}{e}\) 进行了适配。为了确保参数高效性，在每个专家中保持FFN层不变，仅训练适配器模块 \(\mathcal{A}{e}\) 。通过这种方式，只需存储一个FFN副本，保持模型大小不变，除了适配器和路由模块中参数的增加。其余层，例如Norm和Attention，则从密集模型中复制。

\[\begin{equation} \mathcal{A}{e}(x) = \sigma(x W{e}^{down}){W_{e}^{up}} + x. \end{equation} \]

对于给定输入 \(x\) ，路由模块 \(\mathcal{R}\) 根据注意力层的归一化输出 \(x_{in}\) 从 \(N_E\) 个专家中激活 \(\texttt{Top-}k\) 个专家。考虑 \(W_{|\cdot|}\) 表示相应专家模块的权重，将路由模块定义如下：

\[\begin{equation} \mathcal{R}(x_{in}) = \text{Softmax}(\texttt{Top-}k(W_{\mathcal{R}} \cdot x_{in})) \end{equation} \]

\({\tt Open-RAG}\) 模型的高效性源于以下设置： \(|\theta_e| = |W_{e}^{down}| + |W_{e}^{up}| \ll |\phi_o|\) ，其中在微调过程中保持密集LLM的 \(\phi_o\) 不变。

最后，将参数高效的专家模块的输出 \(y\) 表达为：

\[\begin{equation} y = \sum_{e=1}^{N_E} \mathcal{R}(x)_e \mathcal{A}_e (\mathcal{E}_e(x)). \end{equation} \]

混合自适应检索

由于LLM具有不同的参数知识，论文提出了一种混合自适应检索方法，该方法基于模型信心提供两种阈值选择，按需检索并平衡性能和速度。

在训练过程中， \(\mathcal{M}{G}\) 学习生成检索反映标记（[RT] 和 [NoRT]）。在推理时，通过将 [NoRT] 添加到输入中，测量基于强制不检索设置的输出序列 \(o\) 的信心，从而得出 \(\hat{q} = q \oplus \texttt{[NoRT]}\) 。设计了两种不同的信心分数 \(f{|\cdot|}\) ： (i) \(f_{minp}\) ，即单个标记概率的最小值，以及 (ii) \(f_{meanp}\) ，即生成序列中单个标记概率的几何平均值。

\[\begin{align} \label{eq:meanpscore} f_{minp}(o | \hat{q}) &= \min_{i=1}^{m} p(o_i|\hat{q}, o_{<i}) \\ f_{meanp}(o| \hat{q}) &= \sqrt[m]{\prod_{i=1}^{m} p(o_i|\hat{q}, o_{<i})} \end{align} \]

通过可调阈值 \(\gamma\) 控制检索频率，当 \(f_{|\cdot|}<\gamma\) 时进行检索。

主要实验

如果本文对你有帮助，麻烦点个赞或在看呗～

更多内容请关注微信公众号【晓飞的算法工程笔记】

Open-RAG：将开源LLM模型集成为高效RAG模型 | ENMLP'24