医疗花费预测（保姆级教程）

目标

想要一开始快速抓住一个实验的方向，我觉得一个好方法就是抓住实验目的。

本实验：根据一个人的年龄、性别、BMI、子女个数、是否吸烟和生活地区，预测这个人在医疗方面花费的金额。

线性回归

这里我想问个问题，线性回归是什么，或者说针对于DBSCAN聚类算法之后得到的样本，进行线性回归的作用？

线性回归是一种统计分析方法，用于通过一个或多个自变量（特征值）和因变量（目标值）之间的线性关系进行建模

针对本实验：DBSCAN聚类算法可以将数据集划分为不同的簇，线性回归操作为每个簇建立一个特定的线性关系模型，从而更准确地分析和预测每个簇内的数据点。

追根溯源的了解

因为我们小组负责的是三部分：线性回归、结果预测、结果分析。

经过上述的解释，我们会发现，要想实现准确的线性回归、相对合理的结果分析，其实需要从头全方位，做完成前面所有的步骤，包括：数据读取、预处理、分析。

数据读取

import pandas as pd
train = pd.read_csv("E:/《数据分析与可视化》/第6章 医疗花费预测/train.csv")
train.head(5)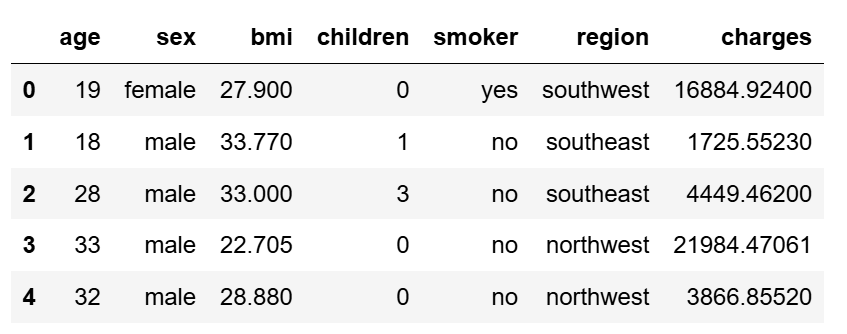

数据预处理

from sklearn.preprocessing import OrdinalEncoder
import numpy as np
encoder = OrdinalEncoder(dtype=np.int)
train[['sex', 'smoker', 'region']] = \
    encoder.fit_transform(train[['sex', 'smoker', 'region']])
train.head(5)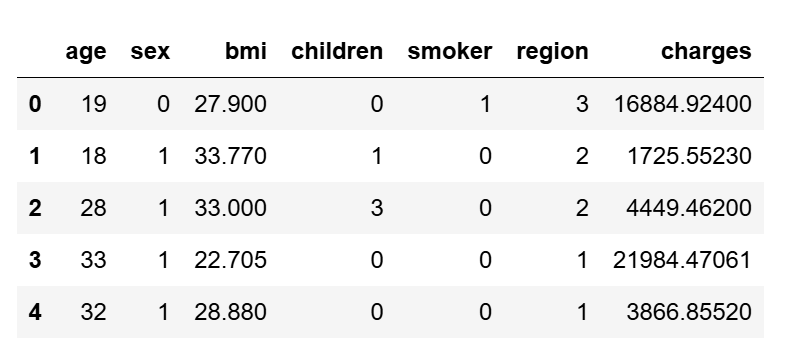

查看数据分布

在处理完字符串类型的转换后,对其余数据进行观察,发现age、bmi和charges属于连续数据,而children是离散数据。

这边老师说过：离散数据是整数等只能取特定值的数据

这边我从导数（瞬时变化率）方面来解释一下：

离散数据：不能直接求导，相邻点的之间只能用差分来求解瞬时变化率

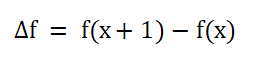
连续数据：能直接求导，用导数来表示瞬时变化率

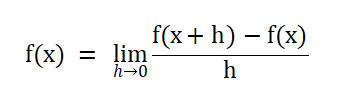
在本案例中,使用seaborn库对连续数据的分布进行可视化：

import seaborn
seaborn.distplot(train['charges'])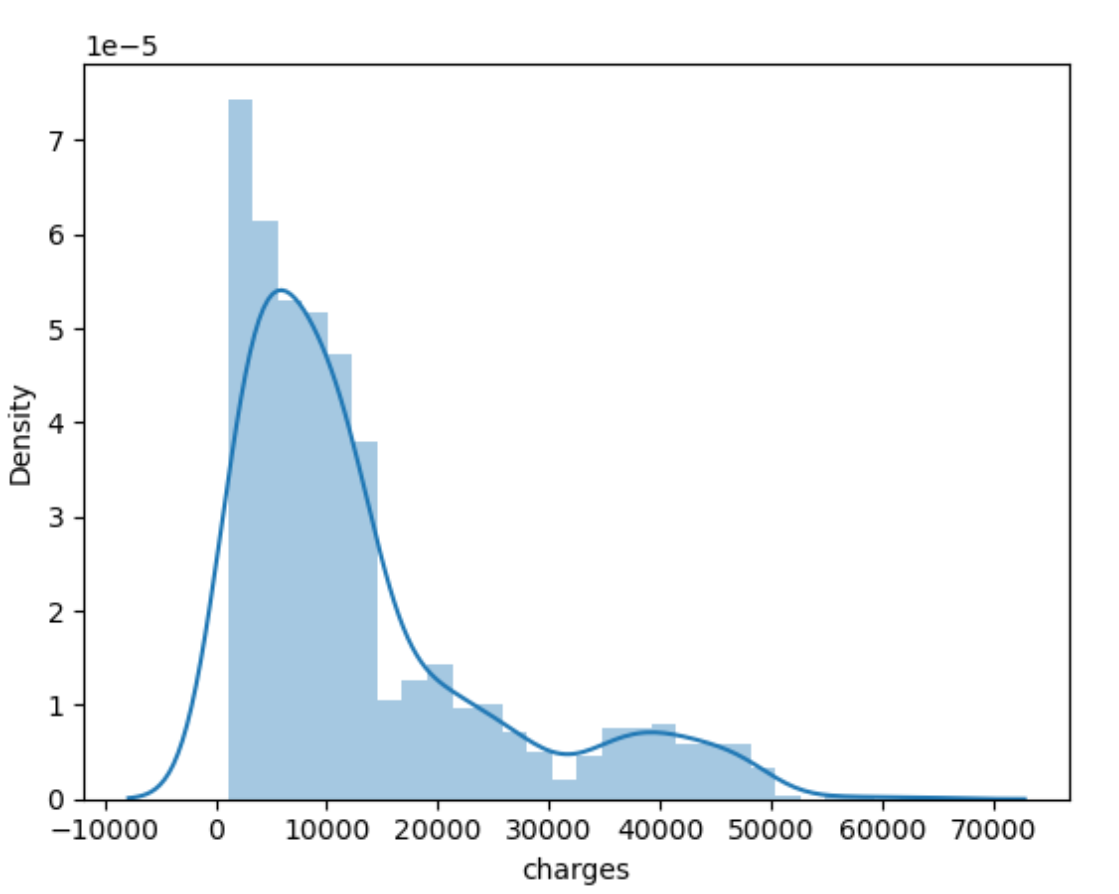

可以看出,charges近似符合对数正态分布,因此对charges取对数,再一次进行可视化charges的对数、age和bmi的可视化结果

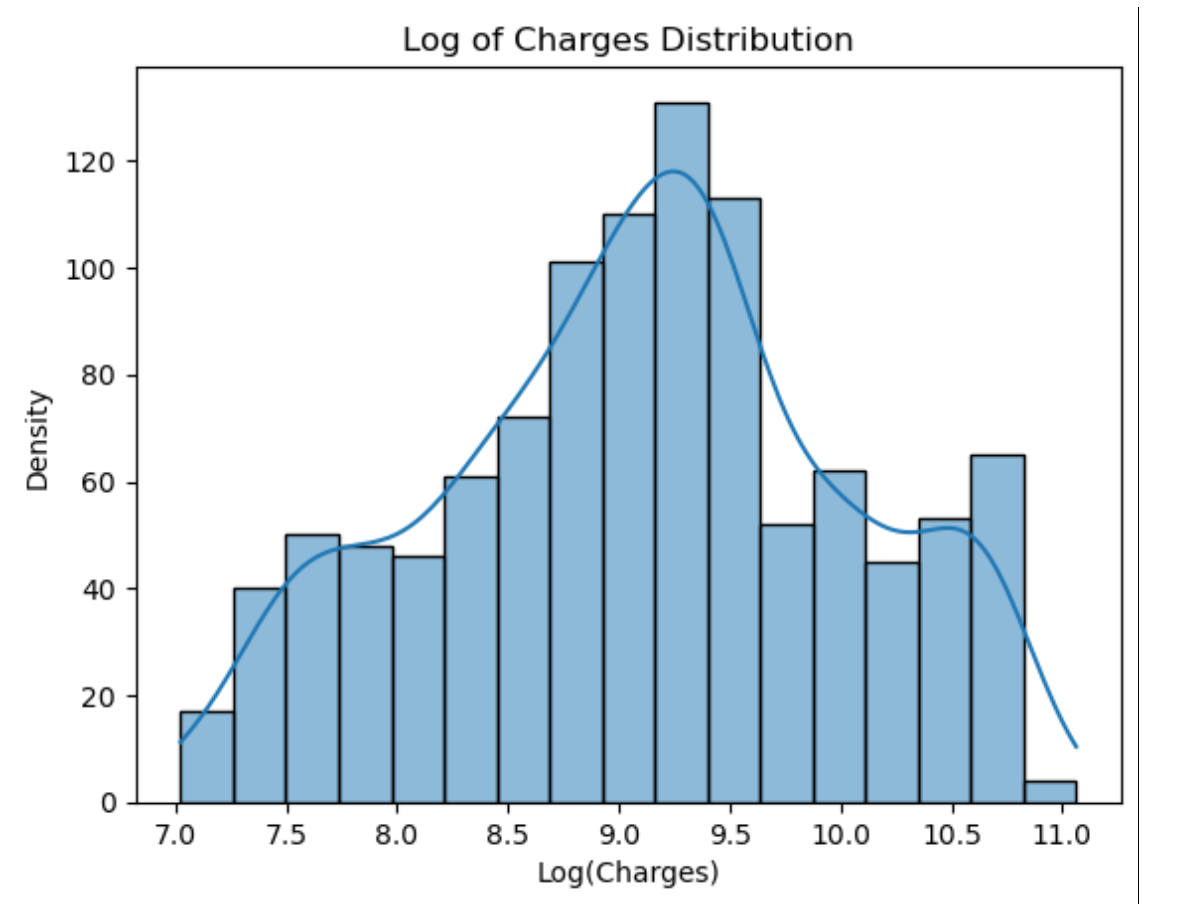
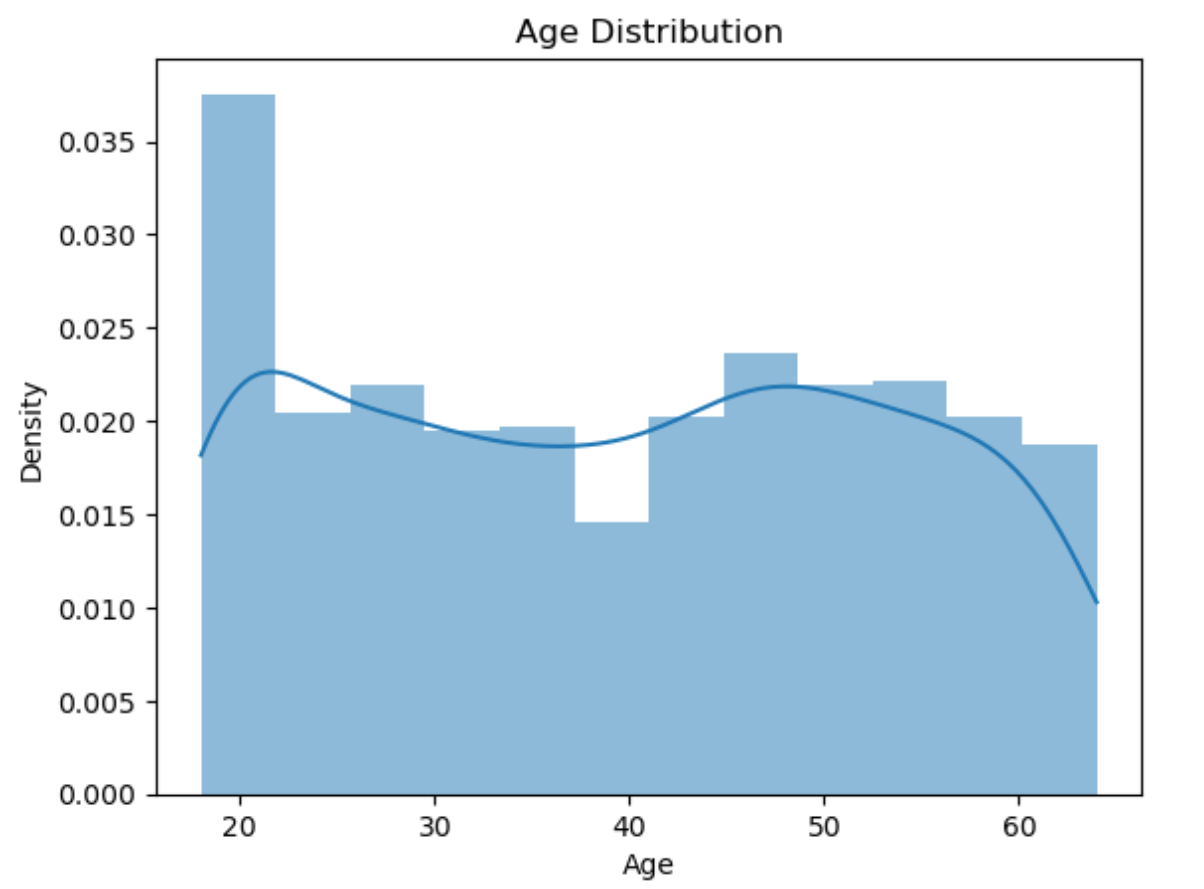
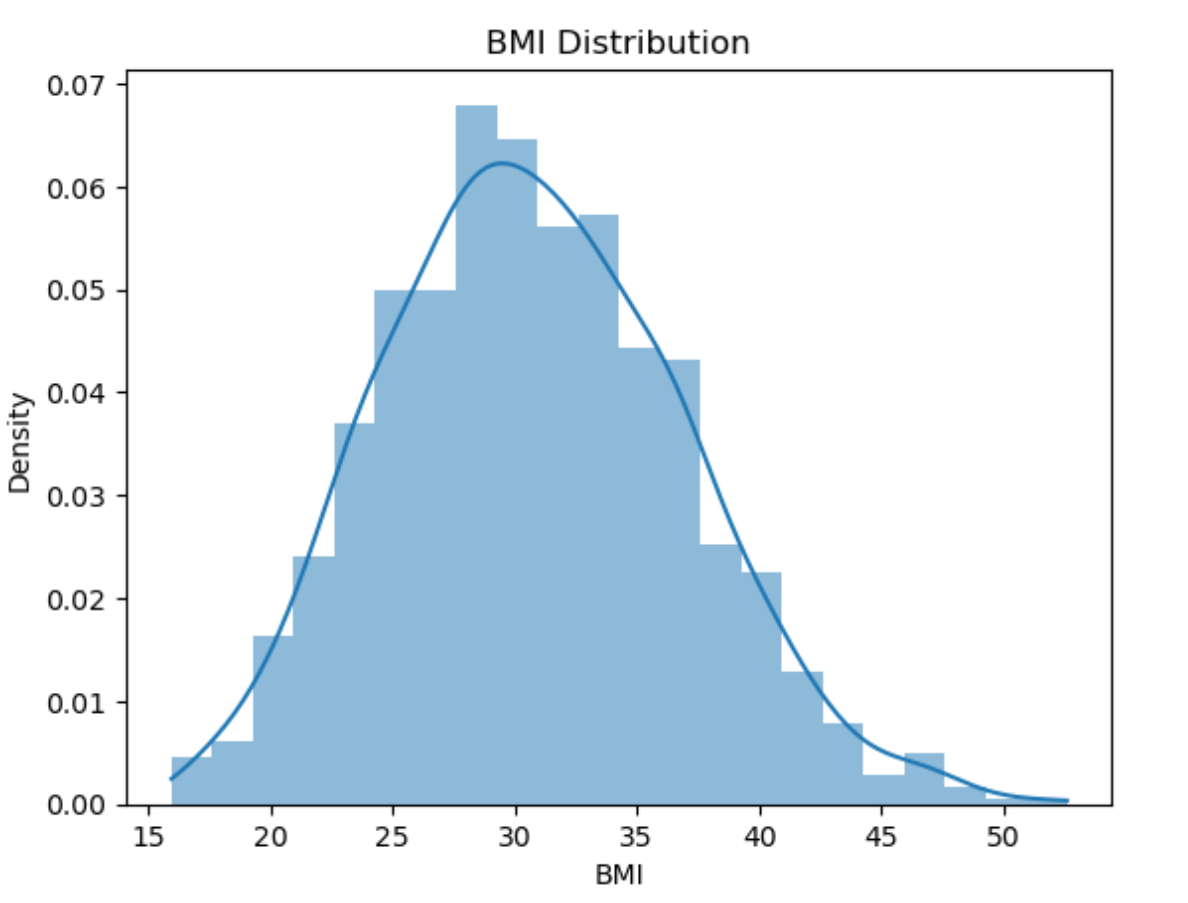
sns.pairplot(train[['log_charges', 'age', 'bmi']])
plt.show()

在这边我因为后文要进行线性关系分析，所以我想要是没有进行聚类，那么结果会是怎么样的。

在这边我运用了pairplot方法，他默认会为每一对变量生成散点图，即使这些变量之间可能没有明显的线性关系，生成了一个3阶图。

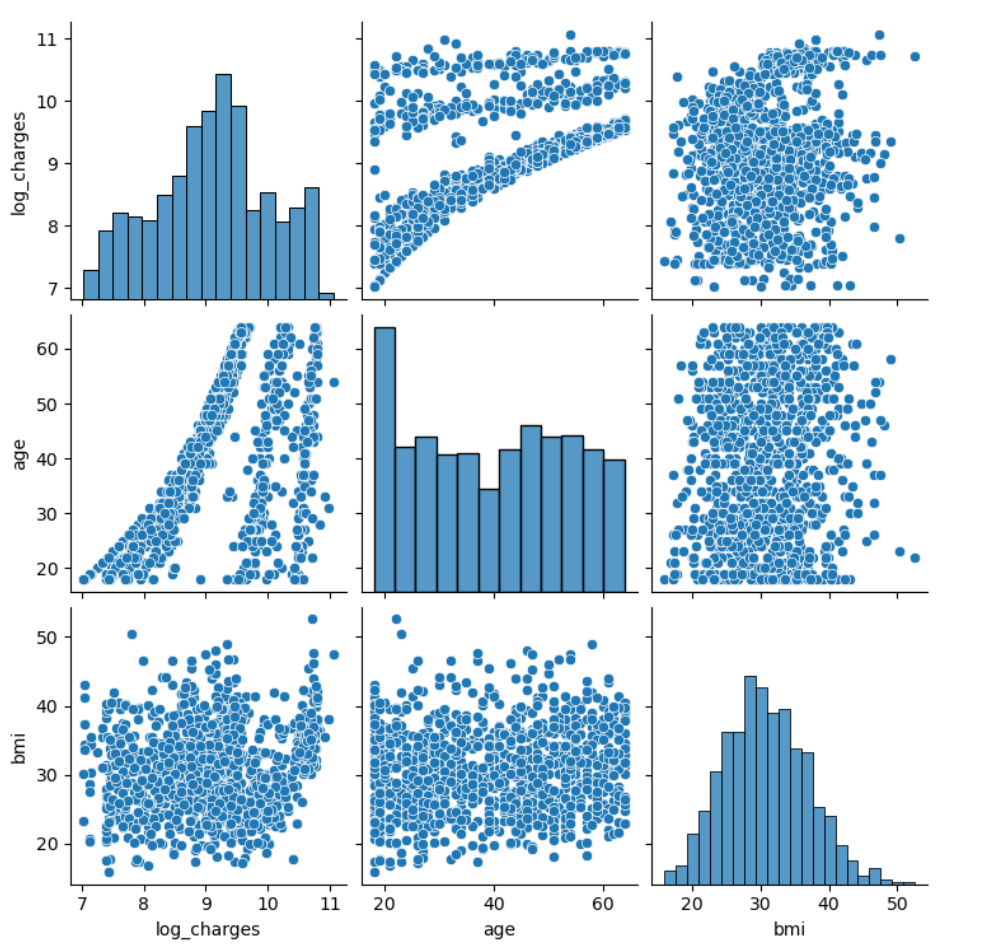
初步结果分析

其实所有聚类方法、线性回归模型，无非都是提高最后结果的精准度，但其实在聚类之前，我们已经可以看出来一点端倪，或者用结果分析更准确。

• log_charges与age之间存在正相关关系，随着年龄的增加，log_charges也增加。
• log_charges与bmi之间的关系不太明显，数据点分布较为分散，没有明显的相关性。
• age与bmi之间也没有明显的相关性，数据点分布较为随机。

相互之间关系的差别，也直接提醒了我们：线性回归模型不能通过链接不同样本来建立，需要对每一个类样本自身进行线性建模，也就是说需要建立三个模型。

from sklearn.preprocessing import MinMaxScaler, StandardScaler
min_max_scaler = MinMaxScaler()
zscore_scaler = StandardScaler()
train['charges'] = np.log(train['charges'])
train[['age']] = min_max_scaler.fit_transform(train[['age']])
train[['bmi', 'charges']] = zscore_scaler.fit_transform(train[['bmi', 'charges']])
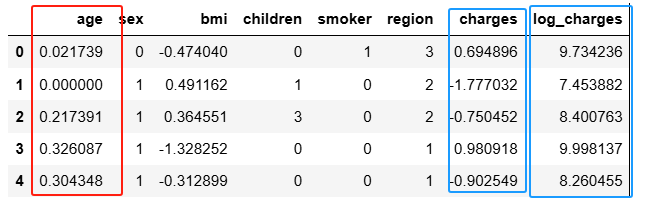
train.head(5)

Min-Max 归一化

使用最大最小值标准化将均匀分布的age映射到区间[0,1]

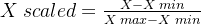
Z-score 标准化

log_chaeges和bmi服从正态分布，使用Z-score标准化方法映射取值

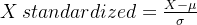
协方差矩阵和热力图

热力图有个有点，通过颜色很直接的反映多个变量之间相关性的强弱

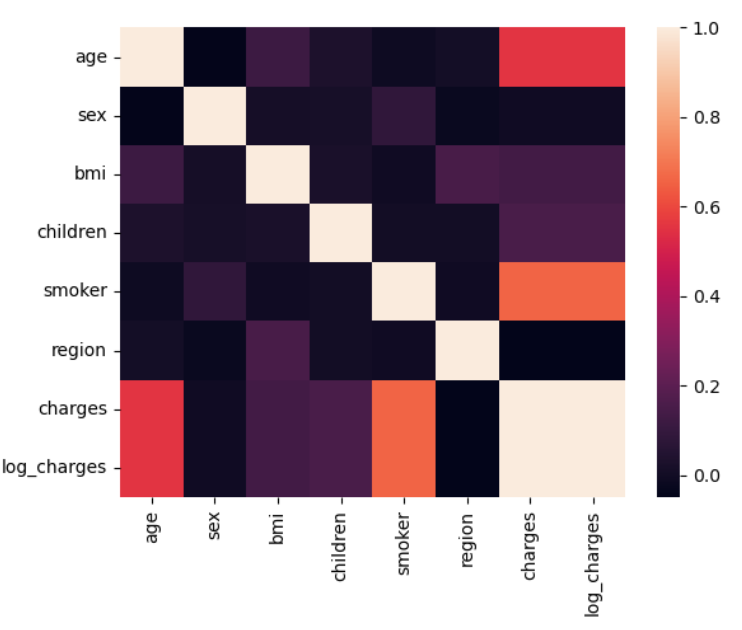
由图可以在我之前的散点图3阶图前面添加一点关系：smoker

DBSCAN聚类算法

针对于密度的聚类算法，通过指定一个虚径e和一个数量阈值M，构造一个圆，在半径范围内超过M数量的点集的点称为核心点；边界点是在半径内e内，但数量不超过M的点集的点；其余是噪点。

通过每个点的大量计算，这个对于人来说工作量太大，将所有核心点标记为同一类别，合成点集。

这边我做一个课外拓展：

大家有没有在概率论的课外学习中，或者竞赛中接触过一个很类似的分类方法，但不是用于聚类的（提示：也是用于求点的）

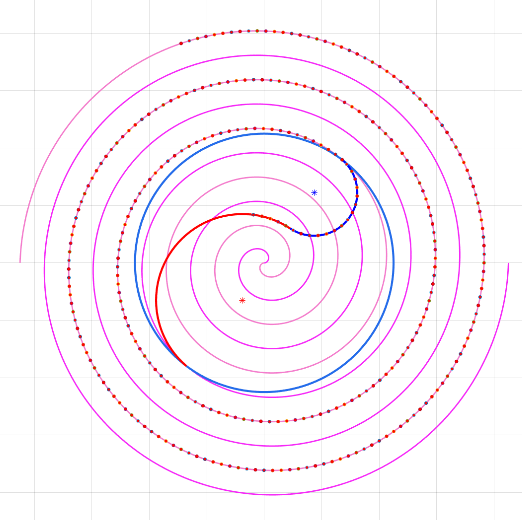
这边是2024年数学建模竞赛A题中的龙舟碰撞问题，这边除了利用四阶龙格库塔方法暴力迭代的方式，我当时想到了另外一种方法，利用蒙特卡洛方法随机生成点，给每个点赋以虚拟半径，随机给点，碰撞后就标红，最后，点最红的（也就是最密集的地方就是核心位置，类似于上述核心点）这样就可以利用其余的边界点和噪点规避碰撞。这俩个方法虽然解决的问题不一样，但是核心解决问题的方式一样，这么好的东西，我们不能仅仅学过就好了，应该内化于心，用于各个问题中实现他多方面的价值）

当然这里面的每一处都涉及数据分析，可视化，这方面也要紧紧掌握。

回归本实验：

def graph3dc(train, x, y, z, type_name="type"):
    ax = plt.figure().add_subplot(111, projection = '3d')
    data = train[train[type_name] == 0]
    ax.scatter(data[x], data[y], data[z], s=10, c='r', marker='.')
    data = train[train[type_name] == 1]
    ax.scatter(data[x], data[y], data[z], s=10, c='g', marker='.')
    data = train[train[type_name] == 2]
    ax.scatter(data[x], data[y], data[z], s=10, c='b', marker='.')
    ax.set_xlabel(x)
    ax.set_ylabel(y)
    ax.set_zlabel(z)
    plt.show()

graph3dc(train, 'age', 'bmi', 'charges')

样本分为3，再次分析age和charges关系

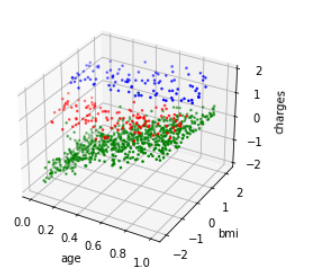
修改参数，观察age和smokers的聚类关系，从而再次验证age、smokers和charges的关系。

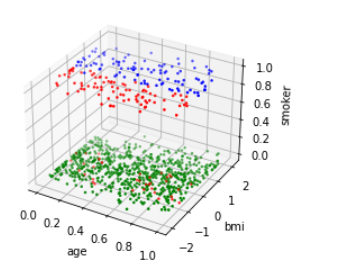
支持向量机分类算法

这边有需要提到上述的蒙特卡洛核心方法，因为他们取点分类的方法压根没有标准，所以仅仅适合得到标签，方便我们进行结果检验和方向选择，通过聚类方法我们知道了age、smokers和charges都有明显的关系，所以基于这个点，我们通过点集之间的相互的影响关系，设立最短距离标准，建立超平面，通过超平面对空间的点进行分类。

from sklearn.svm import SVC

train_svm = train[train["type"] != -1]
svm = SVC(kernel='linear')
svm.fit(train_svm[["age", "bmi", "smoker"]], train_svm["type"])

train["type_predict"] = svm.predict(train[["age", "bmi", "smoker"]])
(train[train["type"] == train["type_predict"]]).shape[0] / train.shape[0]

利用非噪声点对支持向量机进行训练，将DBSCAN聚类的结果作为验证集来对比支持向量机，最后得出的结果约为83%。

线性回归

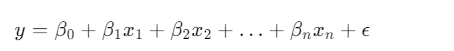
这是线性回归的标准方程

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

train["age2"] = train["age"] ** 2

models = {}
for t in train["type"].unique():
    if t == -1:
        continue
    train_re = train[train["type"] == t]
    models[t] = LinearRegression()
    models[t].fit(train_re[["age", "age2", "bmi"]], train_re["charges"])

train["charges_predict"] = 0
for t in train["type_predict"].unique():
    train.loc[train["type_predict"] == t, "charges_predict"] = \
        models[t].predict(train.loc[train["type_predict"] == t, 
            ["age", "age2", "bmi"]])

mean_squared_error(train["charges"], train["charges_predict"])

其实误差的含义很明显，真实值和预测值的对比，那么这边我们是如何确定预测值的

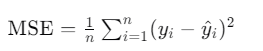
通过该公式，我们可以很明确的算出误差值。

这边我在数学理论检验中，发现一个问题，可能也会有人好奇，根据图像，大家很容易发现age和charges的关系并非简单的线性关系，看起来更像二次函数关系。

那么为什么可以利用线性回归呢？

这边涉及到一点线性代数的知识，也就是多项线性回归：他是线性回归的扩展，允许模型拟合数据中的非线性关系。

那么最后的一点疑惑我们也可以解决了。

结果预测

test = pd.read_csv("test.csv")
submission = test.copy(deep=True)

test[['sex', 'smoker', 'region']] = \
    encoder.transform(test[['sex', 'smoker', 'region']])

test[['age']] = min_max_scaler.transform(test[['age']])
test[['bmi', 'charges']] = zscore_scaler.transform(test[['bmi', 'charges']])

test["type"] = svm.predict(test[["age", "bmi", "smoker"]])

test["age2"] = test["age"] ** 2
for t in test["type"].unique():
    test.loc[test["type"] == t, "charges"] = \
        models[t].predict(test.loc[test["type"] == t, 
            ["age", "age2", "bmi"]])

test[["bmi", "charges"]] = zscore_scaler.inverse_transform(test[["bmi", "charges"]])
submission["charges"] = np.exp(test["charges"])
submission.to_csv('submission.csv', index=False)

结果分析

test = pd.read_csv("test.csv")

seaborn.lineplot(data={'test': test["charges"], 'submission': submission["charges"]})

我们发现模型的预测值和真实值在一些峰值有差别，大致的曲线相同

这个差别，我们需要重回age2这个点、归一化和线性回归模型建立这几个方面。

标准差、方差、最小最大化、type、平均值、标准差、age2非线性化。