1. 前言
这篇博客主要用于记录VAE的原理部分。
一方面便于日后自己的温故学习,另一方面也便于大家的学习和交流。
如有不对之处,欢迎评论区指出错误,你我共同进步学习!
图均引用自4部分的博客!!!!!!!
2. 正文
这篇博客集各博客之长,比较简洁易懂:因为有的博客交代清楚了原理,但损失函数部分比较迷惑,有的是公式比较清晰,但原理比较迷惑,我从我个人的角度,把我认为比较直观的地方做一个总结。
AE(Auto-Encoder)自编码器
VAE(Variational Auto-Encoder)变分自编码器
变分在哪里?

2.1 整体结构
编码器就是想把一个物体投到隐空间,相当于编码的过程,提取输入的特征,用向量的形式表征出来,便于运算。
普通编码器的结构:
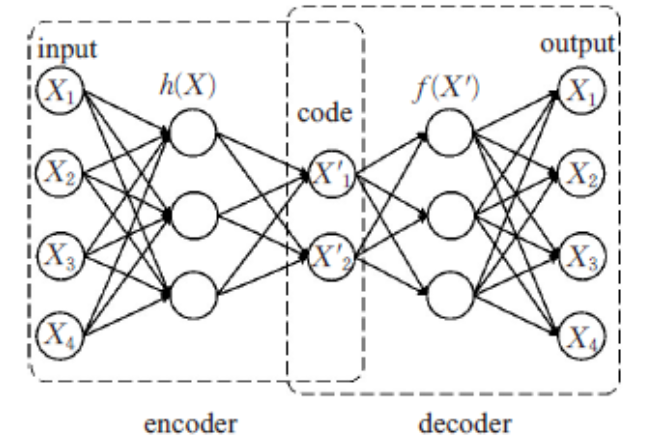
VAE的结构:
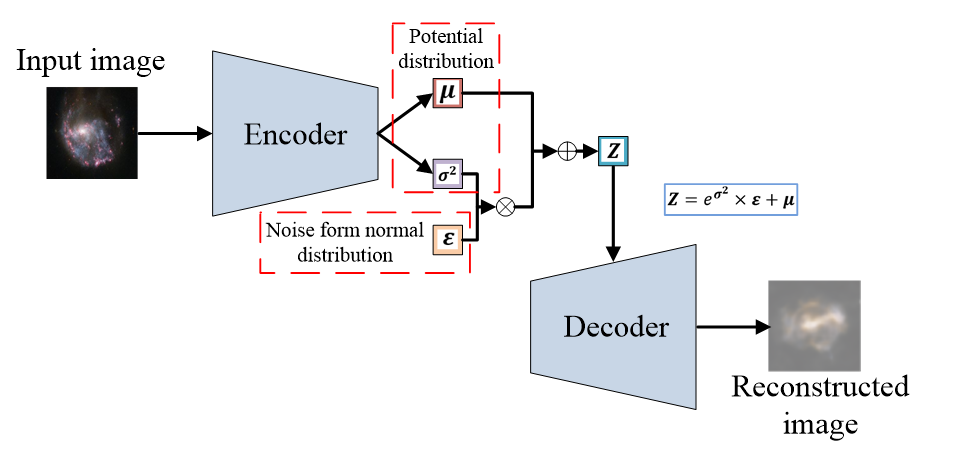
2.2 主要目的
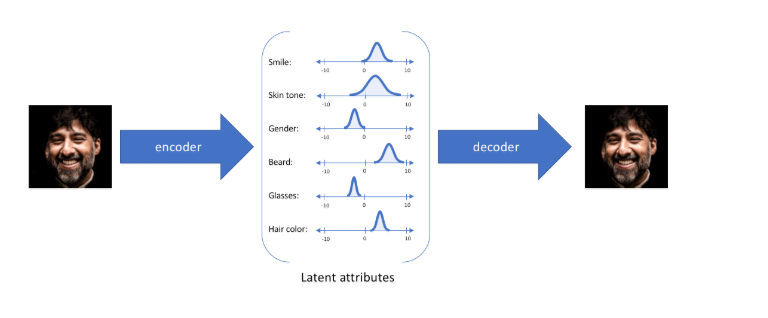
假设任何人像图片都可以由表情、肤色、性别、发型等几个特征的取值来唯一确定,那么我们将一张人像图片输入自动编码器后将会得到这张图片在表情、肤色等特征上的取值的向量X',而后解码器将会根据这些特征的取值重构出原始输入的这张人像图片。
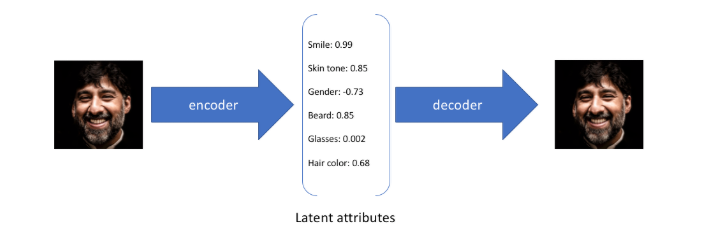
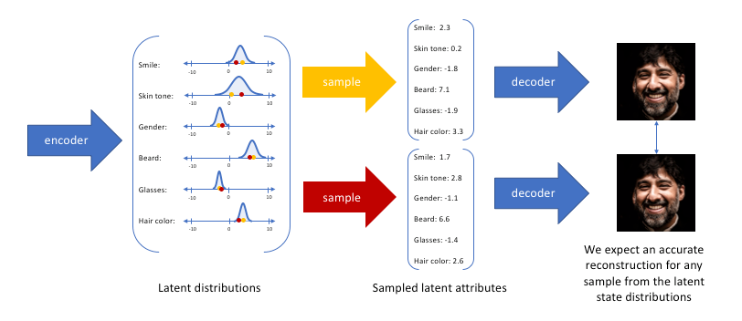
但如果输入蒙娜丽莎的照片,将微笑特征设定为特定的单值(相当于断定蒙娜丽莎笑了或者没笑)显然不如将微笑特征设定为某个取值范围(例如将微笑特征设定为x到y范围内的某个数,这个范围内既有数值可以表示蒙娜丽莎笑了又有数值可以表示蒙娜丽莎没笑)更合适,于是:
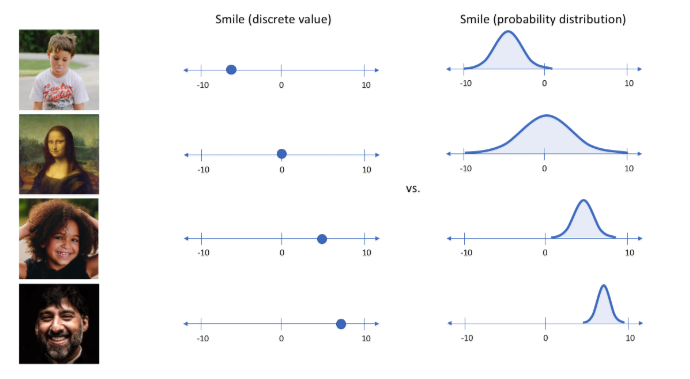
就可以把确定的事件描述为概率分布:
然后最后再采样得到所谓的latent变量Z
2.3 损失函数
再来看一下网络结构:
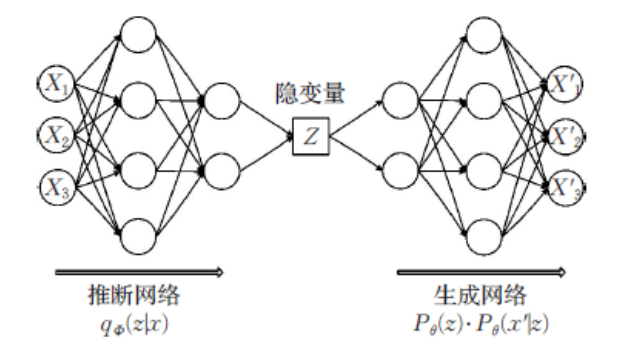
vae的loss函数为两项,重构损失(reconstruct loss)以及kl散度正则项(kl loss),分别对应模型训练过程希望达成的两个目的。
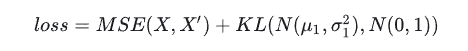
2.3.1
重构损失(reconstruct loss)希望vae生成的结果和输入之间的差异比较小。
2.3.2
kl散度正则项(kl loss)希望编码器生成的隐变量尽可能符合标准正态分布。
为什么呢?详情请查看其他博客的公式推导,因为本文主打一个简洁,公式就不再赘述。

大概也就是下面这个图:
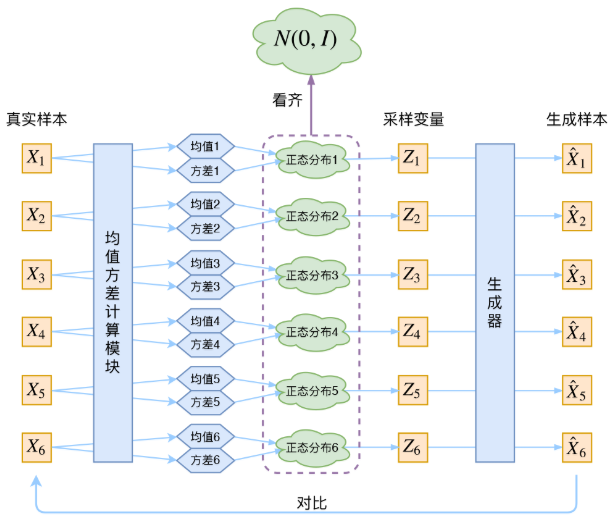
2.4 代码实现
这是pytorch里面的代码实现过程:
class VAE(nn.Module):
def __init__(self):
super(VAE, self).__init__()
self.fc1 = nn.Linear(784, 400)
self.fc21 = nn.Linear(400, 20)
self.fc22 = nn.Linear(400, 20)
self.fc3 = nn.Linear(20, 400)
self.fc4 = nn.Linear(400, 784)
def encode(self, x):
h1 = F.relu(self.fc1(x))
return self.fc21(h1), self.fc22(h1)
def reparameterize(self, mu, logvar):
std = torch.exp(0.5*logvar)
eps = torch.randn_like(std)
return mu + eps*std
def decode(self, z):
h3 = F.relu(self.fc3(z))
return torch.sigmoid(self.fc4(h3))
def forward(self, x):
mu, logvar = self.encode(x.view(-1, 784))
z = self.reparameterize(mu, logvar)
return self.decode(z), mu, logvar给出简单的计算图:
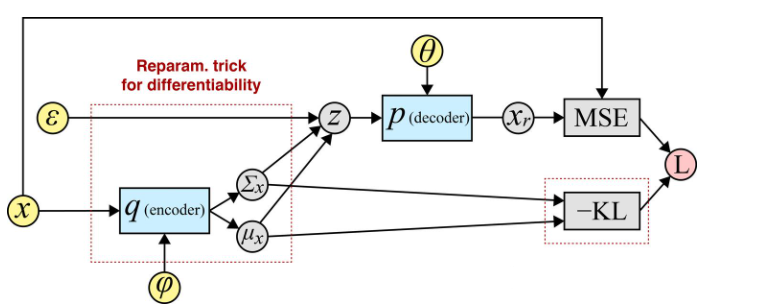
大家对比代码和计算图一起食用,效果更佳!
注意:reparam的代码部分和图的部分对应于我之前的结构图的这个部分:
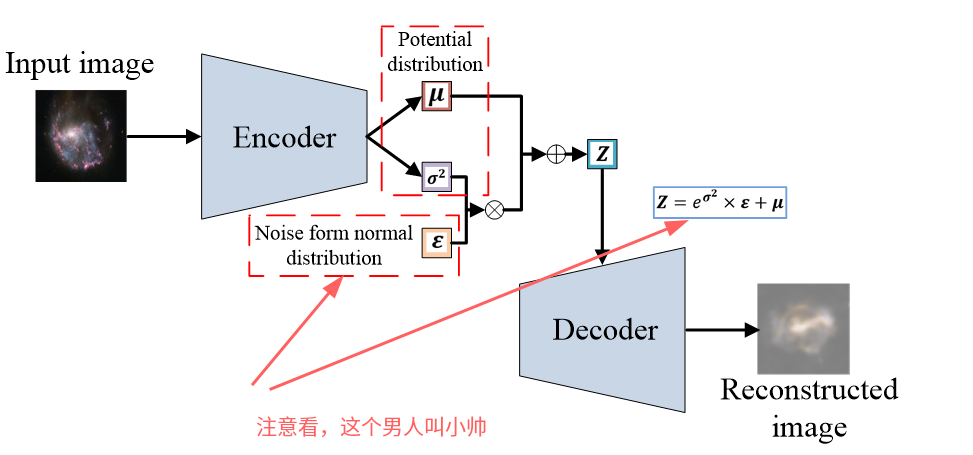
3. 后记
这篇博客点到为止,日后我会继续补充,保证你看完后大概明白其原理而不会像其他博客一样一头雾水,因为笔者把很多博客的精华都提炼出来了。
zsy 2025.1.21
4. Acknowledge
本文参考的博客如下:
https://zhuanlan.zhihu.com/p/64485020
https://zhuanlan.zhihu.com/p/578619659
https://zhuanlan.zhihu.com/p/345360992
https://blog.csdn.net/A2321161581/article/details/140632339
下面这篇博客写的非常详细:
https://spaces.ac.cn/archives/5253