前文先看现象

double的精度损失

老大说：谁要再用double定义商品金额，就自己收拾东西走

先看现象

涉及诸如float或者double这两种浮点型数据的处理时，偶尔总会有一些怪怪的现象，不知道大家注意过没，举几个常见的栗子：

典型现象（一）：条件判断超预期

java 复制代码

System.out.println( 1f == 0.9999999f ); // 打印：false
System.out.println( 1f == 0.99999999f ); // 打印：true

典型现象（二）：数据转换超预期

java 复制代码

float f = 1.1f;
double d = (double) f;
System.out.println(f); // 打印：1.1
System.out.println(d); // 打印：1.100000023841858

典型现象（三）：基本运算超预期

java 复制代码

System.out.println( 0.2 + 0.7 ); // 打印：0.8999999999999999

典型现象（四）：数据自增超预期

java 复制代码

float f1 = 8455263f;
for (int i = 0; i < 5; i++) {
    System.out.println(f1);
    f1++;
}
// 打印：8455263.0
// 打印：8455264.0
// 打印：8455265.0
// 打印：8455266.0
// 打印：8455267.0


float f2 = 84552631f;
for (int i = 0; i < 5; i++) {
    System.out.println(f2);
    f2++;
}
// 打印：8.4552632E7 （纳尼？不是+1了吗？）
// 打印：8.4552632E7
// 打印：8.4552632E7
// 打印：8.4552632E7
// 打印：8.4552632E7

看到没，这些简单场景下的使用情况都很难满足我们的需求，所以说用浮点数（包括double和float）处理问题有非常多隐晦的坑在等着咱们！

怪不得技术总监发狠话：谁要是敢在处理诸如商品金额、订单交易、以及货币计算时用浮点型数据（double/float），直接让我们走人！

Python为什么连0.1+0.2都算不对

python 复制代码

>>> 0.1 + 0.2
0.30000000000000004

>>> 0.1 + 0.2 == 0.3
False

绝大多数编程语言都有这个问题，这是因为电脑的内存是有限的但是数字是无限的，计算机采用二进制保存数据，对于一个16bit大小的存储空间，最多只能保存\(2^{16} = 65536\)个数字。

这明显不够用，怎样在有限的内存中存储更多的数字呢？

在十进制中可以使用科学记数法，比如\(65537 = +6.5537 × 10^4\)、\(0.65537 = +6.5537 × 10^{-1}\)，这样相当大范围的数字只需要这三个元素就可以表示出来

指数
因数
符号

计算机中浮点数的表示方法与此类似，在64bit存储方式中，用1bit存储符号，11bit存储指数，52bit表示分数作为因数。

这种方法就是IEEE 754浮点数标准，遗憾的是这种方法节省了空间却牺牲了精确性，不精确的0.1 + 不精确的0.2 = 更不精确的0.3，更不精确的0.3 ≠ 本来就无法精确表示的0.3，这就是Python连0.1+0.2都算不对的原因了

浮点数在计算机中是如何表示的？

学过 《计算机组成原理》 或者类似 《计算机系统》 这些课程的小伙伴们应该都知道，浮点数在计算机中的存储方式遵循IEEE 754 浮点数计数标准，可以表示为：

\[1.M... × 2^E \]

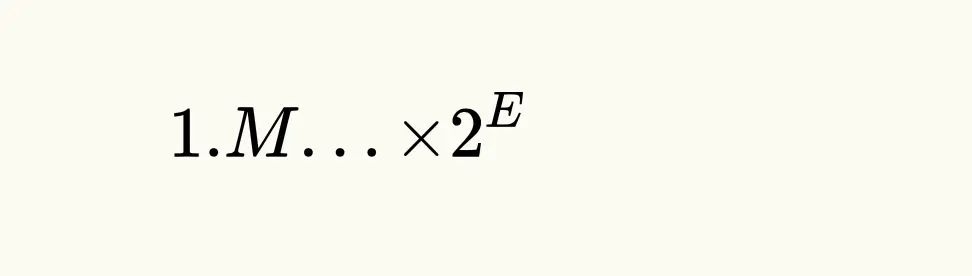
采用尾数 + 阶码 的编码方式，更通俗一点说，就是类似于数学课本上所学的科学计数法 表示方式：有效数字 + 指数位！

因此，只要给出：**符号（S）、阶码部分（E）、尾数部分（M） **这三个维度的信息，一个浮点数的表示就完全确定下来了，所以float和double这两种类型的浮点数在计算机中的存储结构就表示成下图所示这个样子：

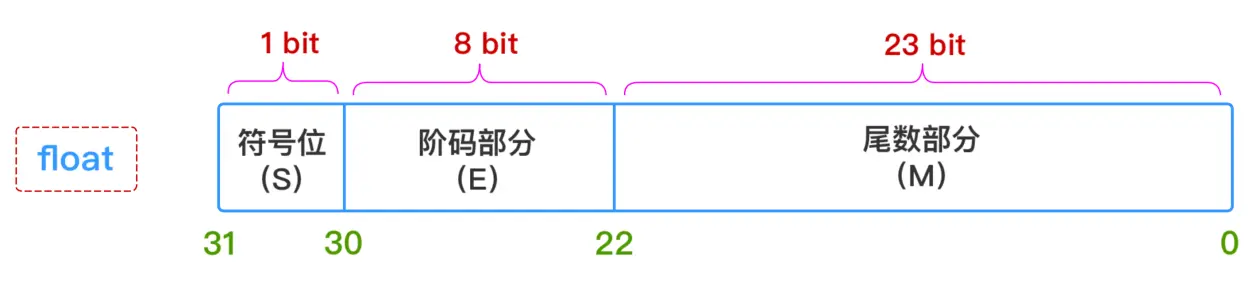
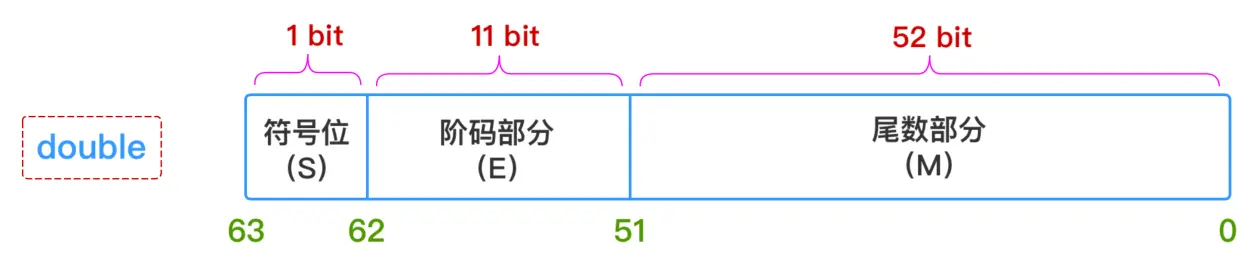
1、符号部分（S）

0：正
1：负

2、阶码部分（E）（指数部分）：

对于float型浮点数，指数部分8位，考虑可正可负，因此可以表示的指数范围为-127 ~ 128
对于double型浮点数，指数部分11位，考虑可正可负，因此可以表示的指数范围为-1023 ~ 1024

3、**尾数部分（M）：**浮点数的精度是由尾数的位数来决定的：

对于float型浮点数，尾数部分23位，换算成十进制就是 \(2^23=8388608\)，所以十进制精度只有6 ~ 7位；
对于double型浮点数，尾数部分52位，换算成十进制就是 \(2^52 = 4503599627370496\)，所以十进制精度只有15 ~ 16位

所以，浮点数交给计算机存储的时候，可能会有精度丢失问题！！！因此使用时需要格外小心，如果真因为这一块出了bug，定位问题还是非常艰难的，所以预防工作要做好。

进制转换计算案例

上面说的是IEEE标准规定的内容，属于理论规约。那一个小数到底要怎么换算成二进制呢？我们得拿实际例子来解释。

先来个简单的例子

比如：把十进制小数0.875转换成二进制，具体怎么操作？

可以分几大步走：

1、以小数点为界，拆分

2、整数部分转换

整数转二进制我想大家应该都熟悉，使用：除2取余法 即可。而这里的0.875整数部分为0，无需操作。

3、小数部分转换

小数部分的转换不同于整数部分，采用的是 "乘2取整法 " ，图示一下就明白了：

4、合并结果

整数部分 + 小数部分，最终得到二进制结果为0.111。

所以该结果按照上一节所述的尾数 + 阶码的计算机计数方式，则可以表示为：

\[1.11 × 2^{-1} \]

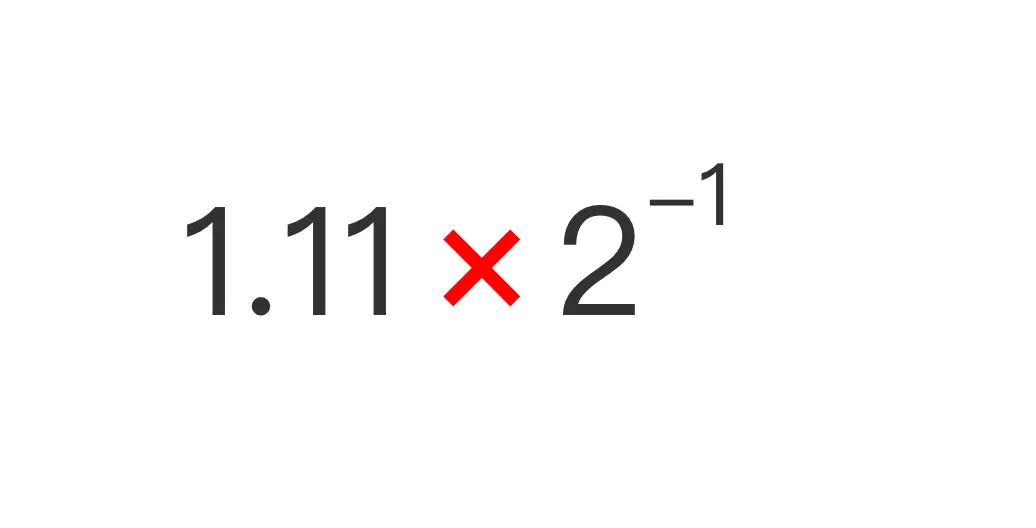
所以对应可得：

符号位：0
阶码（E）部分：若以float为例，应为 127 +（-1）= 126，因此二进制表示为：01111110
尾数部分（M）：若以float为例，应为23位，因此尾部补齐后为11000000000000000000000。

因此最终的总结果为（以32位精度float表示）：00111111011000000000000000000000

再来个复杂点例子

再比如：把十进制小数6.36转换成二进制，具体怎么操作？

但凡能用图示，我就不想写文字，所以用一张图就可以解释得明明白白：

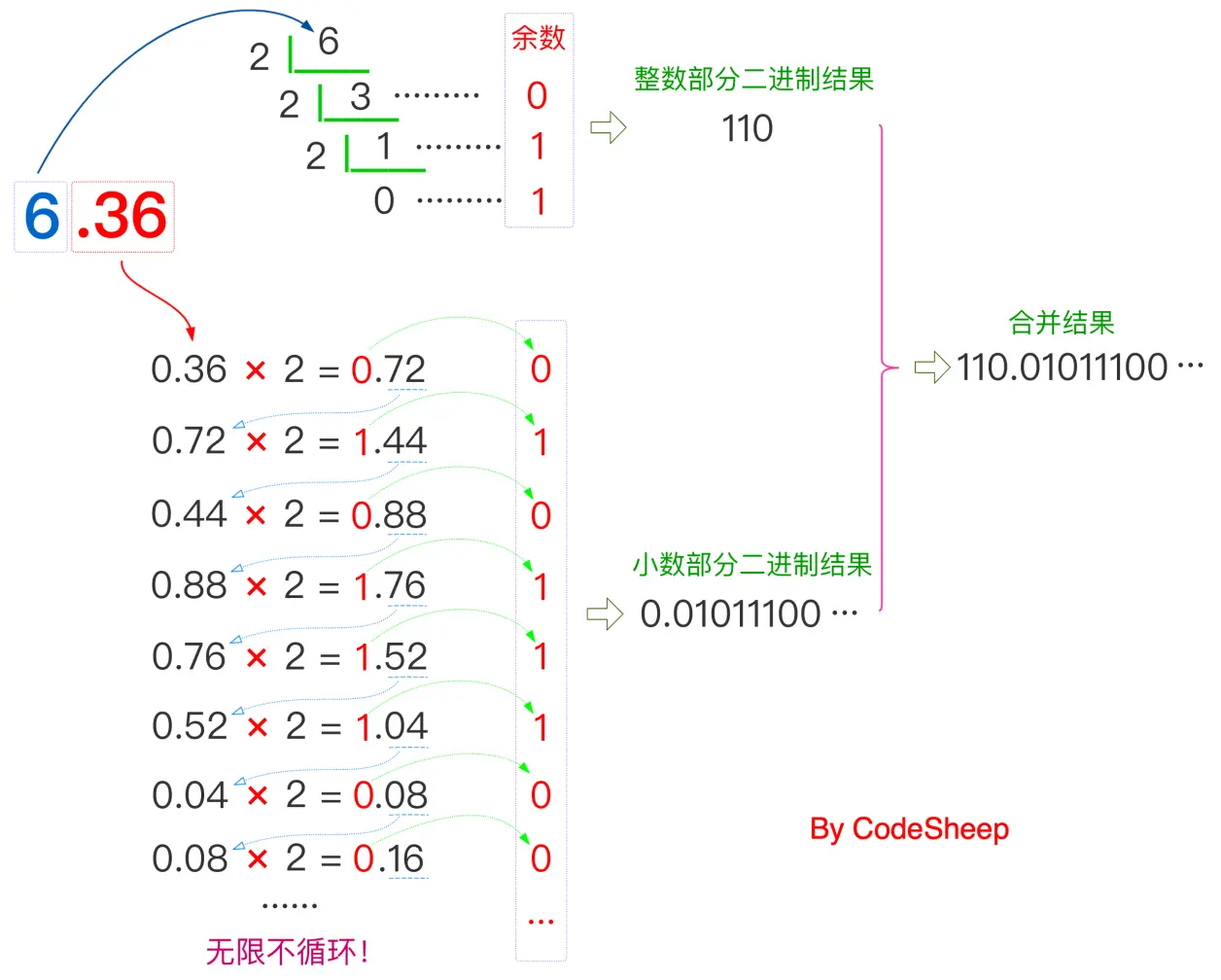
整数部分 + 小数部分，因此最终得到的结果二进制结果为110.01011100...。

还是按照上一节所述的尾数 + 阶码的计算机计数方式，则可以表示为：

\[1.1001011100... × 2^2 \]

所以对应可得：

符号位：0
阶码（E）部分：若以float为例，应为 127 +（2）= 129，因此二进制表示为：10000001
尾数部分（M）：1001011100...，其实它本身无限不循环，但若以float型精度来截取23位，则可以表示为10010111000010100011111

因此最终的总结果为（以32位精度float表示）：01000000110010111000010100011111

所以像这种无限位数的尾数情况，用计算机存储产生截取是必然的，必定会有一定的精度损失！所以这也从根本上解释了为什么float或者double这种类型数据使用时的风险性，因此必须要结合实际业务理性考量。

神器加持

大家如果对上面的计算结果不放心，或者想检查手动换算的结果是否正确，也有直接的这种二进制转换工具站，典型的比如binaryconvert

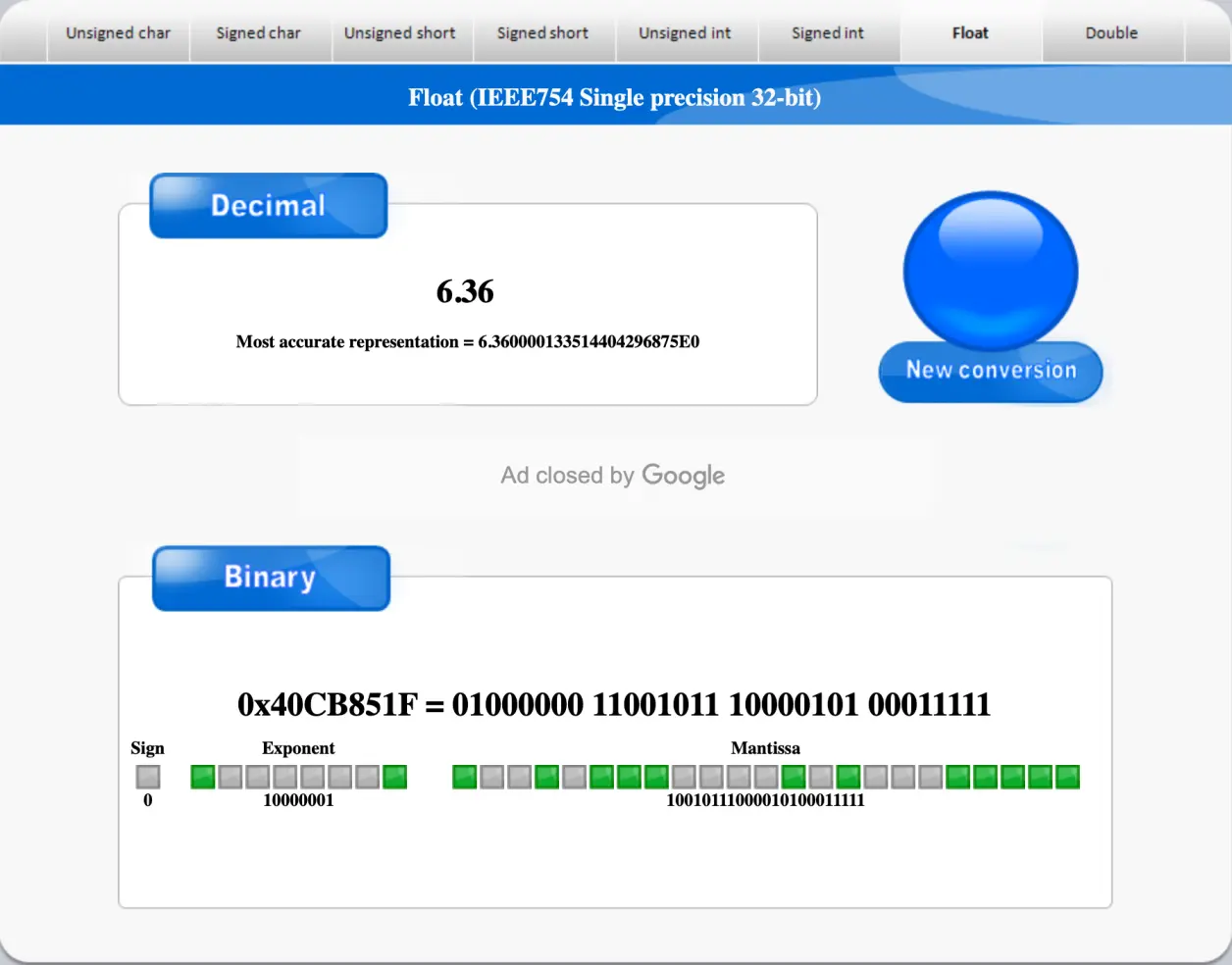
不想手动换算的，直接去上面输入，转换一下即可得到结果，而且可以进制互换，使用非常方便。

IEEE754在线计算工具工具：http://weitz.de/ieee/

IEEE754快速教程：https://zhuanlan.zhihu.com/p/564458140

【计算机组成】浮点数在计算机中的表示与转二进制

前文先看现象

double的精度损失

Python为什么连0.1+0.2都算不对

浮点数在计算机中是如何表示的？

进制转换计算案例

先来个简单的例子

再来个复杂点例子

神器加持