作者:Jacob Ingle
图片由 DALL-E 生成
引言: 本文使用的数据基于知识共享许可协议提供。虽然我们已经尽最大努力确保信息的准确性和完整性,但我们并不保证其完整性或可靠性。数据的使用遵循各自许可协议的条款和条件,任何第三方使用也应该遵循原许可要求。
建议读者详细查看与数据集相关的具体知识共享许可协议,以了解允许的使用方式、修改规定以及署名要求。
本文的项目是一个跟着做的项目,演示如何在不依赖机器学习库的情况下,用 Python 构建你自己的 K-Means 对象
欢迎来到我 DIY AI & ML 系列的第三篇文章!这次,我们将用 Python 搭建一个 K-Means 对象。K-Means 是我最喜欢的机器学习算法之一,因为它能帮我们发现数据中那些看不见的模式。执行得好的话,它能通过严密的数学逻辑,展示出数据中很有意义的分组或聚类。这在现实世界中能带来很多很厉害的应用。
比如说,假设你被要求分析一个电商网站的点击流数据。你就可以利用 K-Means 把客户根据他们点击的东西、加到购物车的东西、或者购买的东西,划分成特定的群体。这可以帮助制定个性化策略,让你根据客户所属的群体,量身定制网站体验。好啦,咱们现在正式进入算法的内容。
K-Means 算法
首先我得提一下,K-Means 算法是个无监督的机器学习算法。无监督机器学习模型的关键特点是:数据中没有目标值或者标签。换句话说,我们不是要预测什么,而是想给数据打上标签。在 K-Means 算法里,我们的目标是把数据分成不同的组或者簇。那这是怎么做到的呢?首先,用户有"自由"去指定要把数据分成多少个簇。我这里加上引号,是因为确定簇的数量时,有些最佳实践要考虑。太少可能会遗漏很多对你的用例有价值的信息;太多的话,可能就变得冗余了。至于怎么分配簇,每个数据点会被分到离它最近的那个簇。底下还有更多细节,咱们接着讲。
关键概念:欧几里得距离
图片来自 Pythagorean Theorem
想想你早期数学课的内容吧。你可能还记得毕达哥拉斯定理:
a² + b² = c²
我们用这个公式来算直角三角形斜边(也就是我当时叫的"最长边")的长度。要得到 c 的准确数值,得对 a² + b² 开方。也许你没意识到,其实理解了这个公式,你也就懂了怎么在坐标平面上计算两点之间的距离!这也是线性代数中的一个概念,叫 L2 范数。比如说,假设你有一个二维坐标平面,x 是横轴,y 是纵轴。给定两点 (x1,y1) 和 (x2,y2),我们可以用这个公式计算它们之间的欧几里得距离:
图片由作者提供
我们也可以在多于二维的空间里计算欧几里得距离。比如说,在三维空间中找两点之间距离的公式是:
图片由作者提供
那这和 K-Means 有什么关系?咱们马上就讲。
质心:初始化、迭代、收敛
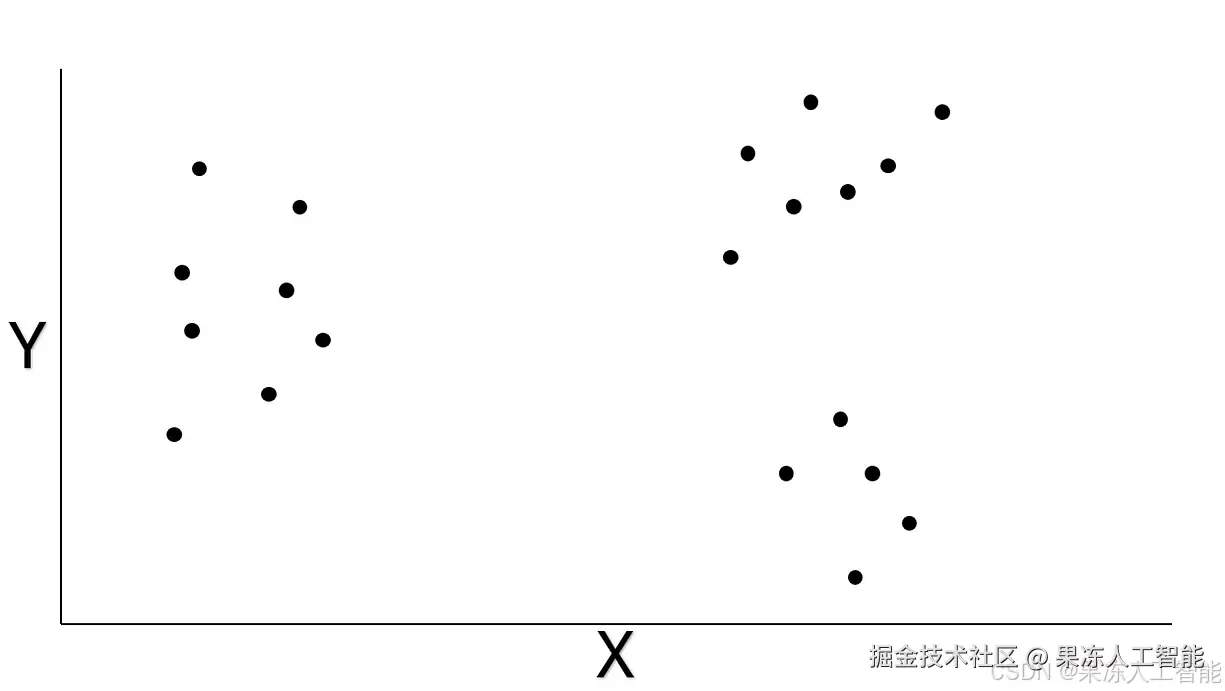
这部分,咱们先拿个简单例子来说明 K-Means 怎么运作。下面这张图,是我随便想的一个二维数据集。如果把这些数据点画出来,大概能一眼看出分组,不太需要用 K-Means 来分。不过为了演示,我还是来走一遍流程。
图片由作者提供
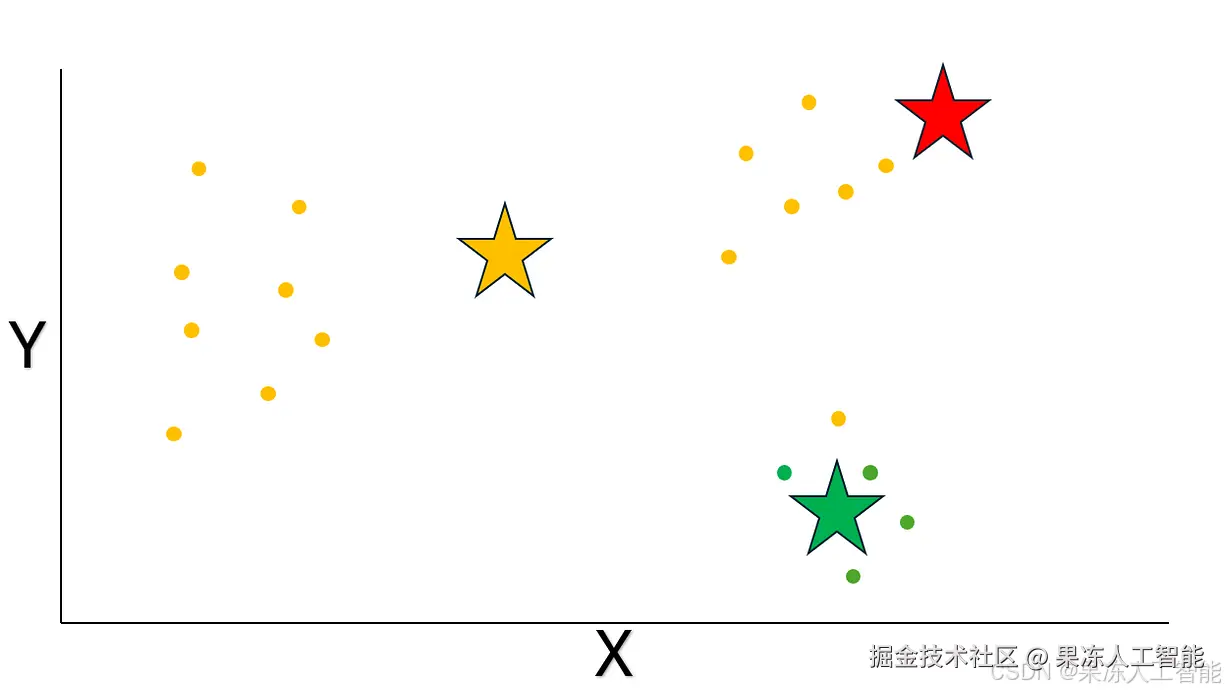
像我前面说的,我们可以指定分成多少个簇。这个例子里,咱们分成 3 个簇。首先,随机生成三个点,作为最初的质心。质心就是代表一个簇中心的坐标。咱们用星形标记这些随机质心:
图片由作者提供
接着,我们要给每个数据点分配质心,也就是看它离哪个质心最近,用欧几里得距离来计算。换句话说,每个数据点被分配到离它最近的质心。看到欧几里得距离在 K-Means 里起到的关键作用了吗?
图片由作者提供
初始化之后,我们要计算每个簇里所有点的均值,得到新的质心坐标。比如说,在一个簇里,把所有点的 x 和 y 坐标分别取平均数,这个新的坐标就成了新的质心或者簇中心。结果大概是这样(注意,红色簇的质心正好落在一个数据点上,因为那个簇只有这一个点):
图片由作者提供
这些簇看着是不是不太对?没关系,咱们还没结束。要一直重复这个过程,直到算法满足特定条件收敛。待会儿详细说。再来一次迭代吧。首先,随机初始化三个质心:
图片由作者提供
然后,按照欧几里得距离,把数据点分配给最近的质心。
最后,重新计算每个簇的新质心:
图片由作者提供
肉眼看,这次 K-Means 算法已经差不多把数据分好了。不过它自己可不知道自己已经收敛了。所以我们还得继续做同样的步骤,并且检查新旧质心的变化。如果新旧质心之间的欧几里得距离差异低于设定的容差(比如 0.0001 这么小的值),我们就可以停止算法,说它收敛了。是不是感觉为什么我一开始要先讲欧几里得距离了?来看收敛的过程吧。
照老规矩,先随机生成质心:
图片由作者提供
给数据点分配最近的质心:
最后,重新计算每个簇的新质心,同时检查新旧质心的距离是否低于容差。这次,距离是 0,说明确实达到了我们的标准,算法收敛了:
图片由作者提供
找到最佳簇数量
现在,给定 k 个簇,我们已经知道怎么把数据正确分成 k 个簇了。不过,还有个问题:最佳的 k 是多少呢?
有几种方法可以用,在我们要构建的 KMeans 对象里,我们会找出能得到最高轮廓系数(silhouette score)的 k。
图片由作者提供
a 是每个数据点到它所在簇质心的平均距离,b 是每个簇质心到最近邻簇质心的平均距离。更通俗点说,轮廓系数越高,说明一个簇内部的数据点彼此之间越靠近、越集中,同时不同簇之间又分得越开。
KMeans 类
现在我们已经讲完了理解 KMeans 算法所需要的所有概念!是时候来构建我们的对象了。先从初始化函数开始。可以看到,我们只会用到 numpy、pandas、tqdm(用来显示进度条),以及 scikit-learn 里的 silhouette_score(放心,就只用 sklearn 里的这一个功能,我们真的会从零构建算法)。下面说说各个属性:
import numpy as np
import pandas as pd
from sklearn.metrics import silhouette_score
from tqdm import tqdm
class DIYKMeans:
def init(self, max_k=10, max_iters=100, tol=1e-4, random_state=None):
self.max_k = max_k
self.max_iters = max_iters
self.tol = tol
self.random_state = random_state
self.k = None
self.centroids = None
self.labels_ = None
self.X_scaled = None
self.feature_means = None
self.feature_stds = None
self.stable_iterations = 0
• max_k:模型要尝试拟合的最大簇数量。
• max_iters:拟合模型时,随机初始化质心的最大次数。
• tol:计算新旧质心距离时的容差阈值。
• random_state:随机数种子,保证可复现。
• k、centroids、labels_:找到最佳 k 后,会赋值这些属性。k 是最佳簇数量,centroids 是最佳 k 的质心坐标,labels_ 是每个数据点的簇标签。
• X_scaled、feature_means、feature_stds:数据的标准化值,以及各特征的均值和标准差。
• stable_iterations:记录在容差范围内稳定迭代次数的占位符。默认要连续 3 次稳定后,才认为算法收敛。
质心操作 & 标准化
接下来这一组方法,就是 K-Means 算法的基本操作啦。看起来应该很眼熟吧?毕竟咱们之前已经讲过了。注意,我们还加了一个数据标准化的方法。为什么重要呢?因为,数据得在同一尺度上,不然尺度大的特征会让算法偏向它们。
比如说,我们想按卧室数、浴室数和房价来聚类房屋。卧室和浴室可能就在 1-5 个房间之间,但价格可能是几十万。如果不标准化,距离计算时价格特征就会完全主导聚类。为了避免这种问题,我们要用标准化,这里用的是均值归一化。
另外,注意我的收敛方法也做了改进。通常算法只要在一次迭代中满足容差就算收敛了,我觉得不太稳,所以设置成连续 3 次满足容差才算真的收敛。
• standardize_data:把每个特征标准化到同一尺度。
• initialize_centroids:给定数据集特征数和 k,随机生成 k 个质心。
• compute_distances:用 numpy 的线性代数库计算欧几里得距离,也就是两个坐标之间形成向量的模。
• assign_clusters:给定一个数据点和质心,返回最近的质心索引。
• compute_new_centroids:根据每个簇的点,分别取各特征的均值,返回新的质心坐标。
• has_converged:给定容差值,检查新旧质心是否在容差范围内。连续 3 次满足,才判定收敛。
def standardize_data(self, X):
self.feature_means = np.mean(X, axis=0)
self.feature_stds = np.std(X, axis=0)
self.feature_stds[self.feature_stds == 0] = 1
return (X - self.feature_means) / self.feature_stds
def initialize_centroids(self, X, k):
np.random.seed(self.random_state)
return X[np.random.choice(X.shape[0], k, replace=False)]
def compute_distances(self, X, centroids):
return np.linalg.norm(X[:, np.newaxis] - centroids, axis=2)
def assign_clusters(self, distances):
return np.argmin(distances, axis=1)
def compute_new_centroids(self, X, labels, k):
return np.array([X[labels == i].mean(axis=0) for i in range(k)])
def has_converged(self, old_centroids, new_centroids, stable_threshold=3):
if np.linalg.norm(new_centroids - old_centroids) < self.tol:
self.stable_iterations += 1
else:
self.stable_iterations = 0
return self.stable_iterations >= stable_threshold
Fit 方法
这是所有步骤真正融合到一起的方法。给定我们设置的 max_k 属性,我们会尝试所有在这个范围内的 k 值。对于每一个 k,我们都会跑一遍迭代流程:随机初始化质心、分配数据点、重新计算质心,一直到收敛为止。同时,我们也会计算每一组聚类的轮廓系数(silhouette score)。哪个 k 的轮廓系数最高,就选哪个作为最终的簇数量。之后,我们就把 k、centroids 和 labels_ 属性赋值成最佳的结果啦。
def fit(self, X):
X = np.array(X)
X = self.standardize_data(X)
self.X_scaled = X
best_k = None
best_score = -1
best_labels = None
best_centroids = None
print("Fitting KMeans across different k values:")
for k in tqdm(range(2, self.max_k + 1), desc="Searching for optimal k"):
centroids = self.initialize_centroids(X, k)
self.stable_iterations = 0
for _ in range(self.max_iters):
distances = self.compute_distances(X, centroids)
labels = self.assign_clusters(distances)
new_centroids = self.compute_new_centroids(X, labels, k)
if self.has_converged(centroids, new_centroids):
break
centroids = new_centroids
score = silhouette_score(X, labels)
if score > best_score:
best_k = k
best_score = score
best_labels = labels
best_centroids = centroids
self.k = best_k
self.centroids = best_centroids
self.labels_ = best_labels
用信用卡数据举个例子
照片来自 Avery Evans,发布在 Unsplash
让我们用 Kaggle 上的一个信用卡数据集来测试我们的 DIY KMeans 对象。
假设你在一家信用卡公司当数据科学家,被分配到一个任务:要识别客户群体。之前,业务团队通常是根据客户的消费类别和平均月余额来划分客户群的。现在领导想要扩展这套逻辑,但又不知道怎么做到规模化。这时候,咱们自己造的 KMeans 对象就派上用场啦。
先导入数据:
data = pd.read_csv('CC GENERAL.csv')
我们有很多特征可以用。不过,为了让业务部门能慢慢适应新的方法,咱们只保留以下这些列。注意,这些定义都是直接从 Kaggle 页面拿下来的:
- BALANCE_FREQUENCY:账户余额更新的频率,分数在 0 到 1 之间(1 = 经常更新,0 = 很少更新)
- PURCHASES_FREQUENCY:购物的频率,分数在 0 到 1 之间(1 = 经常购物,0 = 很少购物)
- CREDIT_LIMIT:用户的信用卡额度
- PAYMENTS:用户的支付金额
- PRCFULLPAYMENT:用户支付全额的百分比
- TENURE:用户持卡时间
cols_to_keep = ['BALANCE_FREQUENCY','PURCHASES_FREQUENCY','CREDIT_LIMIT','PAYMENTS','PRC_FULL_PAYMENT','TENURE']
data_for_kmeans = data[cols_to_keep]
data_for_kmeans = data_for_kmeans.dropna()
快速做个探索性分析,看看这些特征的基本统计信息。这里有几个关键事实:
- 我们有大概 8600 个完整数据的客户样本
- 购物频繁与不频繁的客户大概是 50/50 各占一半
- 大多数客户的信用额度低于 6500 美元
- 大多数客户支付金额在 2000 美元以内,但最高支付到了 50000 美元
- 大多数客户只支付了最多 15% 的账单
- 大多数客户的持卡时间是 12 年,几乎没什么波动
data_for_kmeans.describe()
图片由作者提供
拟合我们自制的 KMeans 模型
现在对数据有了个大致了解,咱们来拟合我们的模型吧!
km = DIYKMeans(max_k=20)
km.fit(X=data_for_kmeans)
图片由作者提供
print('optimal number of clusters: ', km.k)
图片由作者提供
理解聚类的含义
照片来自 Shlomo Shalev,发布在 Unsplash
太好了!我们自制的 KMeans 对象把数据分成了 7 个簇。
但工作远没结束。既然我们已经通过数学方法把客户群分开了,接下来就要探索每个群体里隐藏的关键模式了。
为了做这件事,我自己又写了一个小工具函数,它能输出每个簇的人数、每个特征的均值,还配上热力图,方便对比分析。我在数据集中加了一个叫 'Cluster' 的列,来源是我们 KMeans 对象的 labels_ 属性。
以下是我观察到的一些关键模式:
- 除了第 3 组,其他每一组的客户持卡时间基本都是 12 年。
- 第 2 组是唯一一个高购物频率、高支付比例的群体,信用额度略高于平均水平。
- 第 0、4、5 组的支付比例都很低;但只有第 4 组的购物频率也很低。
- 第 6 组是高消费群体,信用额度最高,支付金额最大。
- 第 5 组在消费水平上和第 6 组接近,但支付金额明显低很多。
根据这些模式,有哪些实际的策略或者方案可以推出来呢?
记住,信用卡公司赚钱,靠的是收手续费和利息。所以,从公司的角度,最好是客户不要一次性全额付清账单,这样能赚点利息,但又不能付太少,否则风险就大了。这里有几个我的小想法:
- 想办法让第 5 组的客户支付比例向第 6 组靠近;
- 考虑给第 2 组客户适度提高信用额度,因为他们支付能力不错;
- 对第 0、4、5 组客户,考虑适当降低信用额度,直到他们的支付比例提高。
data_for_kmeans['Cluster'] = km.labels_
def summarize_by_cluster_with_heatmap(df, cluster_col='Cluster'):
if cluster_col not in df.columns:
raise ValueError(f"Column '{cluster_col}' not found in DataFrame.")
value_cols = [col for col in df.select_dtypes(include='number').columns if col != cluster_col]
if not value_cols:
raise ValueError("No numeric columns to summarize (other than the cluster column).")
grouped = df.groupby(cluster_col)
means = grouped[value_cols].mean().round(2).add_suffix('_mean')
counts = grouped.size().to_frame('count')
summary = pd.concat([counts, means], axis=1).reset_index()
return summary.style.background_gradient(cmap='YlGnBu', subset=summary.columns[1:]).format("{:.2f}")
summarize_by_cluster_with_heatmap(df=data_for_kmeans)
图片由作者提供