在线段树中,我们常常需要维护数组区间上的信息,比如区间和、区间最大值或区间最小值。通过将数组分割成若干子区间,我们实现了对区间的高效查询和更新操作。线段树之所以高效,是因为每次操作只需要处理树上的少数节点,查询和修改操作复杂度均为 \(O(\log n)\)。
但如果问题不再局限于数组区间 ,而是转移到树结构 之上呢?例如,我们希望维护树上从节点 \(u\) 到节点 \(v\) 的路径上每个节点的信息(查询和修改),这时候线段树直接套用已经行不通了。
树上路径和数组的转换
与数组不同的是,树上的节点并不存在连续的线性关系,每个节点可能存在多个子节点,整体呈现分支结构。节点 \(u\) 到节点 \(v\) 的路径信息,包括它们的最近公共祖先(LCA)分别到他们的路径,沿着路径遍历。这等价于在数组 \(O(n)\),显然对于大规模数据是无法接受的。
为了解决这个问题,我们迫切需要一种高效的方法,使得在树上的路径维护操作(如区间修改、区间查询)能够达到类似线段树般的复杂度水平。于是,树链剖分便应运而生。
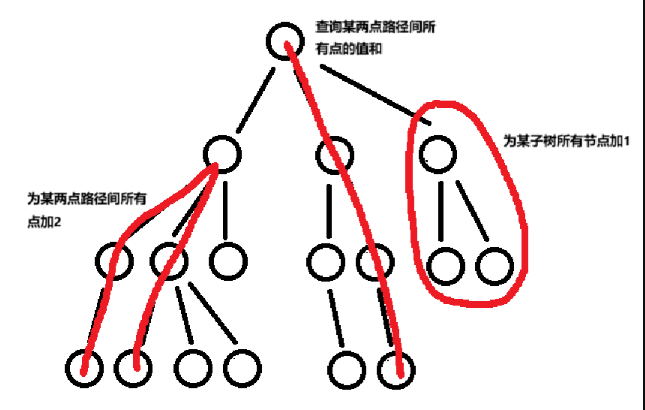
树链剖分原理:长子继承法
在树上进行路径维护时,如果我们仍然沿用朴素的方法逐条路径查询,效率将十分低下。为了让树也可以享受线段树的高效,我们要怎样给树上的节点赋值下标呢?
树链剖分的思想是:将一棵树划分成若干条链,使得树上的路径能够高效地被分解为若干条连续的链,以便利用高效的数据结构(例如线段树)维护链上的信息。
具体而言,我们将树中的边划分为两类:
- 重边 :连接父亲节点与其子节点中子树大小最大的那条边。
- 轻边:连接父亲节点与其余子节点的边。
- 重链:由重边连接成的链
每个节点将它所有子节点中子树最大的"长子"作为重儿子(一样大则任选一个),这样一代代"长子继承",形成了若干条长长的"世袭"链条,余下的为短短的轻链。接下来按照 dfs 的访问时间戳来为节点赋值,每个子树都总是首先访问自己的重边儿子
实现上,按惯例来讲,进行树链剖分通常需要两次遍历。
步骤一:第一次DFS(预处理树的基础信息)
假定我们用邻接表存储树(存储所有儿子)。首先,我们需要遍历整棵树以收集每个节点的基本信息,包括:
- 每个节点的父节点
- 节点深度
- 子树大小
- 重儿子
步骤二:第二次DFS(重链划分)
我们掌握了树中每个节点的子树大小、深度信息以及确定了每个节点的重儿子。第二步是核心,我们要为节点分配时间戳 \(\text {dfn}_x\),并且将节点划分到各个链当中:
- 标记每个节点所属的链顶 \(\text{top}[x]\)
- 为每个节点分配DFS序号 \(\text{dfn}[x]\)(也称为时间戳)
在进行链划分时,我们总是优先进入重儿子,然后再进入轻儿子们,以保持链的连续性,保证同一重链上的节点DFS序连续,而搜索顺序就是他们在新数据结构里(如线段树)的编号。
cpp
class Tree {
struct Node {
int size, fa, hson, top, dfn, dep;
vector<int> to;
};
int n, root;
vector<Node> nodes;
void dfs1(int u, int fa) {
nodes[u].fa = fa;
nodes[u].size = 1;
for (int v : nodes[u].to) {
if (v == fa) continue;
dfs1(v, u);
nodes[u].size += nodes[v].size;
if (nodes[v].size > nodes[nodes[u].hson].size) {
nodes[u].hson = v;
}
}
}
void dfs2(int u, int fa, int &idx) {
nodes[u].dfn = idx++;
nodes[u].top = (nodes[u].hson == -1) ? u : nodes[nodes[u].hson].top;
for (int v : nodes[u].to) {
if (v == fa) continue;
dfs2(v, u, idx);
}
}
public:
Tree(int n, int root): n(n), nodes(n), root(root) {}
void addEdge(int u, int v) {
nodes[u].to.push_back(v);
nodes[v].to.push_back(u);
}
void hld() {
dfs1(root, -1);
int idx = 0;
dfs2(root, -1, idx);
}
};执行完上述两个DFS过程之后,我们就完成了树链的划分,每个节点被划入一条重链或形成轻链。
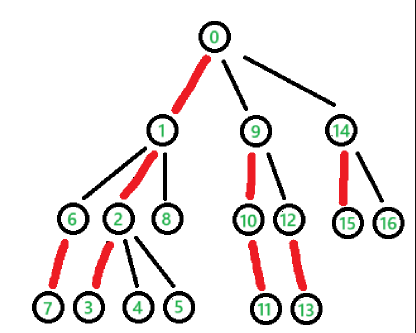
树链剖分的性质与复杂度
通过两次DFS剖分后,我们的轻重链划分和时间戳拥有这些性质,主要体现在以下几个重要性质上:
性质1:每个节点唯一属于某条重链
把一个单独叶节点也视为重链的情况下,每个节点被明确划入了一条重链,由 \(\text{top}[x]\) 标识。而一条轻边总可以连接两条重链。
性质2:DFS序(时间戳)的连续性
同一个子树内的节点,其DFS序(即时间戳 \(\text{dfn}[x]\) )必然连续。同一条重链上的节点,其DFS序也必然连续。这意味着一条重链(或一个子树)的维护(如将所有点修改、查询)可以转化为线段树的区间维护。
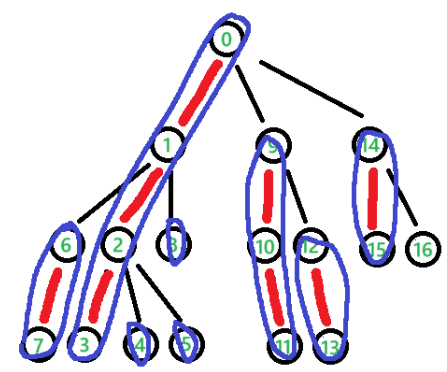
性质3:树上任意两点路径最多经过 \(O(\log n)\) 条重链
这是树链剖分最核心的性质之一。 每个节点到根节点路径上经过的轻链数目不会超过 \(O(\log n)\),因此从任意节点到另一节点的路径也最多经过 \(O(\log n)\) 条重链。
这是因为,每个节点到根节点的路径上,每经过轻链时子树大小至少减半(因为轻链连接的是轻儿子,其不是最终的儿子,大小一定大于父节点的一半)
有了以上性质后,我们可以将树上路径维护问题转化为最多\(O(\log n)\)次区间维护问题:
假设我们需要维护节点 \(u\) 到节点 \(v\) 的路径,要将其拆分为多条重链。我们可以不断将节点所在的链顶深度较深的节点上跳至链顶节点的父亲,直到两节点处于同一条重链中为止:
cpp
void path(int u, int v) {
while (nodes[u].top != nodes[v].top) {
if (nodes[nodes[u].top].dep < nodes[nodes[v].top].dep) swap(u, v);
// 处理重链里 u 到 top[u] 部分
u = nodes[nodes[u].top].fa;
}
if (nodes[u].dfn > nodes[v].dfn) swap(u, v);
// 处理重链里 u 到 v 部分
}通过上述方法,路径查询或修改问题被成功地转化为线段树上最多 \(O(\log n)\) 次的区间维护操作。
树链剖分的复杂度分析
树链剖分的效率主要分为两个阶段:
-
预处理阶段:
- 进行两次DFS,复杂度显然为 \(O(n)\)。
- 构建线段树或其他数据结构,复杂度通常为 \(O(n)\)。
-
单次操作阶段(路径查询或修改):
- 单次路径维护最多涉及 \(O(\log n)\) 条链。
- 每次涉及链上的区间维护,线段树复杂度为 \(O(\log n)\)。
- 故总复杂度为 \(O(\log^2 n)\)。
总结一下树链剖分的复杂度为:
| 阶段 | 操作内容 | 时间复杂度 |
|---|---|---|
| 预处理 | 两次DFS + 数据结构构建 | \(O(n)\) |
| 单次维护 | 路径修改或查询 | \(O(\log^2 n)\) |
通常 \(O(\log^2 n)\) 已经能很好满足绝大多数树上问题的需求了,而树链剖分实现难度适中,因此应用十分广泛。
树链剖分与 LCA
树链剖分由于天然维护了树的链状结构和深度信息,可以用来高效求解LCA问题。既然之前都已经实现求解两点间的路径并分为少量重链了。求解 LCA 实际上更简单。
回忆一下我们上一节讲到的树链剖分的重要性质:树上的任意一条路径可以被分解为最多 \(O(\log n)\) 条连续的链段。
这意味着,当我们需要求解两个节点 \(u\) 与 \(v\) 的 LCA 时,可以沿着重链迅速地将两个节点"上跳"到同一条重链,然后再简单判断二者的深度即可确定 LCA。
具体的求解过程如下:
- 若两个节点不在同一重链,选择较深的节点,将该节点跳到其当前链顶的父节点。
- 重复第1步,直到两个节点在同一条重链内。
- 此时,深度较小的节点即为所求LCA。
cpp
int lca(int u, int v) {
while (nodes[u].top != nodes[v].top) {
if (nodes[nodes[u].top].dep < nodes[nodes[v].top].dep) swap(u, v);
u = nodes[nodes[u].top].fa;
} return (nodes[u].dfn < nodes[v].dfn) ? u : v;
}树链剖分求LCA与其他方法的对比
LCA问题有多种经典算法,包括:
- 倍增法(Binary Lifting)
- Tarjan 离线算法(基于并查集)
- 欧拉序+RMQ方法
- 树链剖分方法
下面我们将树链剖分求LCA方法与这些常用方法进行比较:
| 方法 | 预处理复杂度 | 单次查询复杂度 | 优势 | 劣势 | 在线性 |
|---|---|---|---|---|---|
| 树链剖分 | \(O(n)\) | \(O(\log n)\) | 实现简单,便于与其他树链剖分任务结合 | 单次复杂度略高于RMQ | 在线 |
| 倍增法 | \(O(n \log n)\) | \(O(\log n)\) | 实现直观 | 实践中常数稍大 | 在线 |
| Tarjan算法 | \(O(n+q)\)(离线) | 均摊\(O(1)\) | 单次查询最快 | 离线处理,无法实时回答 | 离线 |
| 欧拉序+RMQ | \(O(n \log n)\) | \(O(1)\) | 在线查询效率最高 | 需额外处理RMQ问题,空间较大 | 在线 |
我们可以看到,树链剖分虽然单次查询复杂度略高于欧拉序+RMQ方法,但优势也很明显:
- 与树链剖分的其他操作(路径修改、查询)相结合极其自然。
- 实现简单,便于维护和扩展。
- 不需要额外的大空间,数据结构也统一。
因此,在实际编程竞赛或工程应用中,如果已经采用了树链剖分维护其他树上问题,那么使用树链剖分直接求LCA通常是一个很好的选择。