博弈游戏,也有很多人把它叫做博弈论,但是博弈论的英文确实和 Game 这个词有关,所以也可以说是博弈游戏。
博弈游戏可以看作是一个专门的小领域(例如 数论、图论、或者是概率论),它的板块非常非常大。
所以这篇文章所写的可能只是很小的一部分,这里先开一个坑,我以后再来填写。
如果我没有听错的话,博弈游戏的全部介绍的书,好像有 800 多页。所以我们这些人学的都是冰山一角。
ICG 游戏
ICG 游戏是一个类别,也只是博弈游戏里面很简单的一类。
ICG,顾名思义,就是公平组合游戏。
这个概念怎么判断呢?它有着几个条件:
-
两个人玩,即恰好有两个玩家。轮流行动。
-
信息是公开的,即目前游戏的状态大家都知道。
-
行动与当前游戏的状态有关(即与当前是哪个玩家是无关的)。
-
举个例子,你和我在玩国际象棋。你的车只能上下左右走,但是我可以说我开了 VIP,可以让车斜着走!
-
这样显然不是 ICG 游戏,因为 可以对车执行的行动 和玩家是谁有关。这也是所谓的公平。你只能横着走,我可以斜着走,公平吗?
-
-
同一个状态不能重复出现。
-
游戏一定会结束(没有平局,只有一个人胜)。且两个人成功的目标一致。
我们来看几个例子,看一下他们到底是不是 ICG。这一点很重要!如果我们面对的游戏不是 ICG 游戏,那么后面的一些理论也不可以用了。
扫雷:不满足第一条,不是 ICG。
麻将:首先不满足第一条,其次也不满足第三条(每个人的牌都可能不同)。
象棋 :虽然这是两个人的游戏,虽然有公开的棋盘,虽然公平,但是可能会出现死局的情况(例如最终只剩下两个将了,完全就结束不了)。
NP 态
注意,这个时候我们讨论的是 ICG 游戏。
NP 是不是能够让你们想到 NP 问题,很抱歉,这里没有任何的联系。
既然 ICG 游戏已经要求最终一定要分出胜负,所以就设两个状态:N 态 和 P 态。
如果游戏的某一个状态是 N 态,则达到这个状态之后的先手必胜(所以所有人都尽量不走到为 N 态的状态,因为这样相当于给对方送命!)。
如果游戏的某一个状态是 P 态,则达到这个状态之后的先手必败(所以所有人都尽量走到为 P 态的状态,因为这样相当于自己必胜!)。
可以证明 ICG 游戏中,任何一个状态要么就是先手一定会胜利,要么就是先手一定会失败。
接下来我们来看几个经典的游戏。
在 DAG 上面的 ICG 游戏
当这个游戏是 ICG 游戏,且状态形成的关系构成一个有向无环图(DAG),就可以使用 NP 态很容易地求解必胜策略和必败策略。
注意,在这里求解 NP 态的时候,我们必须要化身"先知者",首先需要得知可以到达的所有的状态 NP 态分别是什么,再决定自己的 NP 态。
这个 DAG 的每一个点都是游戏的某个状态,每一条边都是游戏状态的变换(即如果我能通过游戏给出的操作把状态 1 变成状态 2,则连 状态 1 \(\to\) 状态 2 的一条边)。
于是这个游戏的行动就变成了**在 DAG 上面,从当前点选一条边走。**这是对于任何 ICG 且状态可以形成一个 DAG 的游戏都适用的。
设我们有这个 DAG。
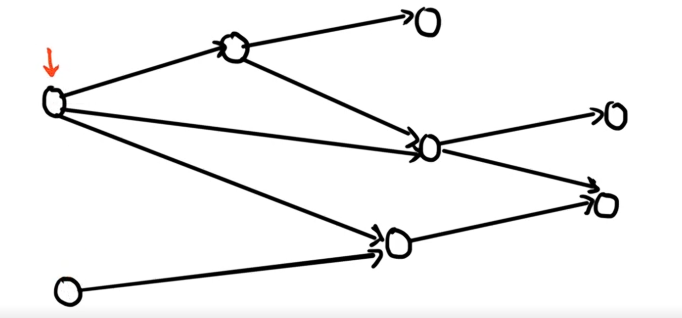
我们需要对于每一个点求出从这个点开始,最终是否必胜还是必败。即求出每一个点的 NP 态。
不妨设游戏终止条件为:不能走就是输了。
注意,这里我只是为了让读者理解一下 NP 态的转移策略,实际上游戏的终止条件各不相同,需要具体问题具体分析。
显然穷途末路的几个点一定是先手必败的,因为走到这些点就不会再有出路。
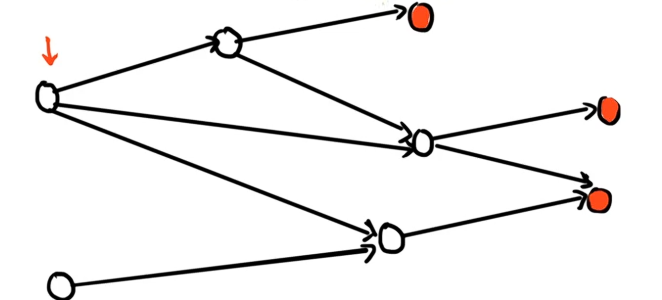
设 P 态为红色,N 态为绿色。
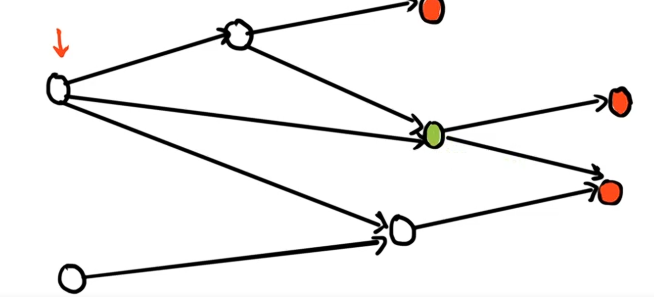
考虑那个画绿色的点。
显然它往哪走都可以,因为哪里走都是 P 态。
于是,这里我们得出:**只要我们的这个状态能够到达一个 P 态的状态,这个状态就一定先手必胜。**这是容易理解的。
同理:
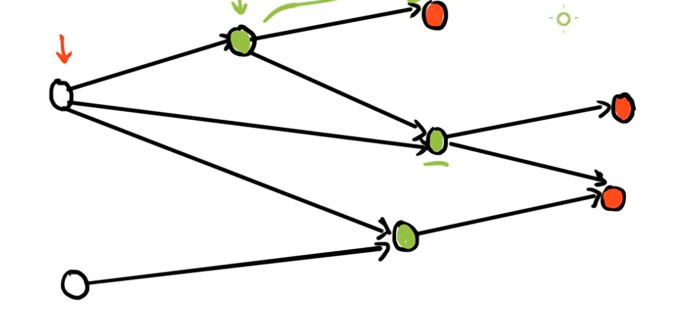
对于绿色点中的最上面的那个点,它虽然也会到达一个绿色点,但是它不走那个绿色点不就行了!它明明可以到达那个红色点的,所以它也是 N 态。
考虑标了红色箭头的点。
显然,它不能到达任何的红色点,而它往哪里走都是绿色点,即后手一定胜,先手一定败。所以,它是 N 态。下面的那一个点同理。
所以,我们又可以得出另外一个真理:如果这个点只能到达绿色点,这个点一定是 P 态。
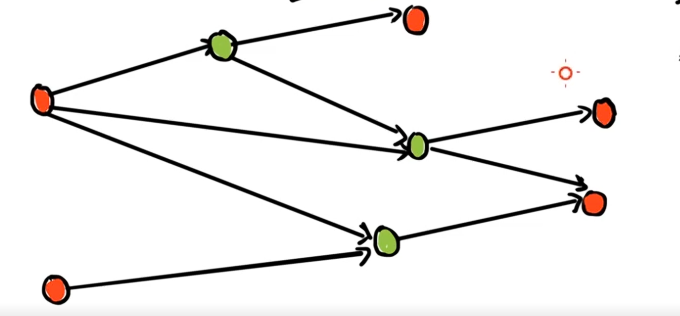
整合起来,NP 态的转移关系满足:
-
N 态:后继结点有 P 态。
-
P 态:后继结点全是 N 态。
还是那句话,NP 态并不适用于所有的博弈游戏。它只适用于只有必胜和必败的情况。
举个例子,还记得那道CSP-S T2,策略游戏吗,就是那道 6 个 ST 表的题目。但是这个题目只能化身"先知者",大力分类讨论,但是不能使用 NP 态了。因为这个游戏没有胜负。
Bash 博弈
我们来看几个很经典的博弈例子。
Bash 博弈:有 \(n\) 个石子,每次可以取 \([1,k]\) 个,不能取的人输。
很熟悉对吧???结论很简单,就是如果 \((k+1) | n\),则先手必败。否则先手必胜。
考虑从 DAG 的视角来看这个问题。设 \(n=7,k=2\),显然可以建出如下的图:
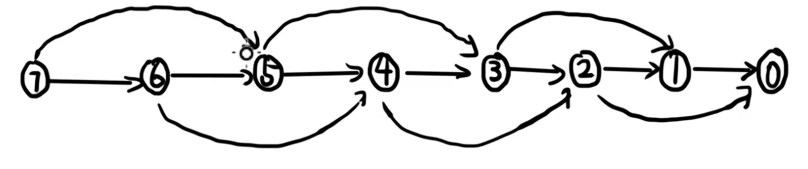
然后就变成了一个 DAG 上面的博弈。
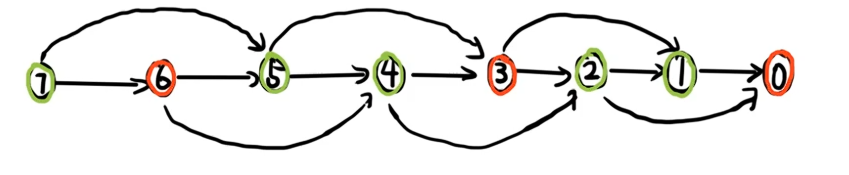
显然可以得出。
显然有必胜策略:把石子数量取成 \(k+1\) 的倍数,然后一直保持 \(k+1\) 的倍数就可以获胜。
威佐夫博弈
威佐夫博弈,英文 wythoff game。
模型描述:有两堆石子,分别有 \(x\) 个和 \(y\) 个(\(x \le y\)),每次可以取一堆的任意数量或者两堆的相同数量,不能取的人输。
最终的结论很奇妙:
-
如果 \(x = \lfloor \frac{\sqrt 5 +1}{2} \rfloor \times (y-x)\),则先手必胜。
-
否则先手必败。
这个东西的黄金比哪来的呢?对不起。
这个东西很恶行,虽然最终的结论很奇妙,但是其证明很繁琐很复杂,这里就不再阐述了。
威佐夫博弈的证明里面有:click here
斐波那契博弈
模型描述:有 \(n\) 个式子,第一次可以取 \([1,n-1]\),以后每一次都最多只能取到上一次的两倍,不能取的人输。
考虑枚举!
1 是显然可以的。
2 是不行的,3 也是不行的。
4 是可以的。
5 的话呢,如果一开始取 1,则不行。一开始取 2,对面可以取 3,也不行。
这下看出来规律了吗:当 \(n\) 是斐波那契数的时候,一定先手必败。否则先手必胜。
尼姆博弈
前面我们讲得都是非常偏僻的内容,尼姆博弈(Nim Game)才是 ICG 游戏中最核心的部分,包括以后博弈论很常用的 SG 函数也需要使用尼姆博弈的结论。
模型描述:有 \(n\) 堆石子,每一次可以选一堆区任意的数量(\(>1\)),不能取的输。
结论:当 \(n\) 堆石子的异或和 \(=0\),先手必败。当异或和 \(\not = 0\),先手必胜。
结论很简单,但是怎么证明呢?
考虑对于一个可能是正确的必败条件,考虑怎么分析。
显然,如果目前已经满足了这个必败条件,则需要证明怎么操作最终都会输掉。
而对于所有输掉的游戏,其一开始的状态存在满足这个必败条件。
显然到了所谓的必败条件的时候(即异或和为 \(0\)),则么走都不会一步内再使得异或和为 \(0\),这是显然的。
而根据 NP 态的转移关系,这样子一定是 P 态。
这是比较好证明的。
所以我们可以证明,如果目前已经满足了这个必败条件,则怎么操作最终都会输掉。
不好证明的在于后面的那一部分。看上面的文章即可。
阶梯尼姆
阶梯尼姆,英文 Staircase Nim。
模型描述:有 \(n\) 堆式子,每一次可以取一堆的任意数量,然后放入前一堆中(第一堆要放入第 \(0\) 堆中),不能选就是输了。
思想很简单:偶数位作为垃圾桶。
然后,奇数位就相当于一个 Nim 模型了。就是这么简单。
考虑证明。如果奇数位到了偶数位就相当于从奇数位里面取出来一些东西,和 Nim 一样。如果偶数位有回到了奇数位,我们还可以再从奇数位丢掉从而进行操作还原,做了和没做一样。
战斗结束。
反尼姆
反尼姆游戏,英文 Anti Nim。
模型描述:有 \(n\) 堆石子,每一次可以选一堆取任意数量(大于 \(1\)),不能取赢。
结论:
-
如果石子数全为 \(1\) 且 \(n\) 为偶数则必胜
-
如果石子数不是全为 \(1\) 而且异或和不等于 \(0\) 则也必胜
-
否则必败。
CF1215D Ticket Game
我们来看一道题。
这道题里面的游戏就不是 ICG 游戏了,因为两个人的目标不一致。怎么办呢?
这道题也告诉我们了如何思考博弈论题目。
考虑一下,如果两个人分别选了两边的 ?:
先手博弈策略:一定会选择对差值增大有利的选项。
后手博弈策略:跟先手选一样,来弥补差值。
所以左右的 ? 会两两抵消,那么剩下的 ? 都会出现在一边。此时问题似乎已经简化许多了。
显然这一边的问号数量一定是偶数。
那么现在:
设现在的差值为 \(dis\),? 的数量为 \(num\),则按照两者的关系分类讨论:
-
\(num / 2 \times 9 < dis\):先手不断选 \(0\) 就可以赢,后手会不断地选 \(9\)。
-
\(num / 2 \times 9 > dis\):先手不断选 \(9\) 就可以赢,后手会不断地选 \(0\)。
-
\(num / 2 \times 9 = dis\):后手只要不断地选和先手相加等于 \(9\) 的情况即可。后手必胜。
于是就直接分类讨论即可。