探秘Transformer系列之(30)--- 投机解码
目录
- [探秘Transformer系列之(30)--- 投机解码](#探秘Transformer系列之(30)--- 投机解码)
- [0x00 概述](#0x00 概述)
- [0x01 背景](#0x01 背景)
- [1.1 问题](#1.1 问题)
- [1.2 自回归解码](#1.2 自回归解码)
- [0x02 定义 & 历史](#0x02 定义 & 历史)
- [2.1 投机解码](#2.1 投机解码)
- [2.2 发展历史](#2.2 发展历史)
- [0x03 Blockwise Parallel Decoding](#0x03 Blockwise Parallel Decoding)
- [3.1 动机](#3.1 动机)
- [3.2 思路](#3.2 思路)
- [3.3 架构](#3.3 架构)
- [3.4 训练](#3.4 训练)
- [3.5 步骤](#3.5 步骤)
- [3.6 优化](#3.6 优化)
- [3.7 收益](#3.7 收益)
- [0x04 原理](#0x04 原理)
- [0x05 算法](#0x05 算法)
- [5.1 总体流程](#5.1 总体流程)
- [5.2 关键步骤](#5.2 关键步骤)
- [5.2.1 前置条件](#5.2.1 前置条件)
- [5.2.2 第一步 - 采样](#5.2.2 第一步 - 采样)
- [5.2.3 第二步 - 并行运行目标模型](#5.2.3 第二步 - 并行运行目标模型)
- [5.2.4 第三步 - 计算接受的猜测token数量](#5.2.4 第三步 - 计算接受的猜测token数量)
- [5.2.5 第四步 - 调整概率分布](#5.2.5 第四步 - 调整概率分布)
- [5.2.6 第五步 - 返回生成的结果](#5.2.6 第五步 - 返回生成的结果)
- [5.3 重点分析](#5.3 重点分析)
- [0x06 实现](#0x06 实现)
- [6.1 全局循环](#6.1 全局循环)
- [6.2 外层逻辑](#6.2 外层逻辑)
- [6.3 实施算法](#6.3 实施算法)
- [0x07 Token Tree Verification](#0x07 Token Tree Verification)
- [7.1 问题](#7.1 问题)
- [7.1.1 采样多个序列](#7.1.1 采样多个序列)
- [7.1.2 验证多个序列](#7.1.2 验证多个序列)
- [7.2 思路](#7.2 思路)
- [7.2.1 开山之作SpecInfer](#7.2.1 开山之作SpecInfer)
- [7.2.2 如何组织树](#7.2.2 如何组织树)
- [7.3 Attention Mask](#7.3 Attention Mask)
- [7.1 问题](#7.1 问题)
- [0xFF 参考](#0xFF 参考)
0x00 概述
投机解码(Speculative Decoding)也叫预测解码/投机采样,它会利用小模型来预测大型模型的行为,从而提升模型在解码(decoding)阶段的解码效率问题,加速大型模型的执行。其核心思路如下图所示,首先以低成本的方式(以小模型为主,也有多头,检索,Early Exit 等方式)快速生成多个候选 Token(串行序列、树、多头树等),然后通过一次并行验证阶段快速验证多个 Token的正确性,只要平均每个 Step 验证的 Token 数 > 1,就可以一次性生成多个token,进而减少总的 Decoding 步数,实现加速的目的。
下图左侧是自回归解码模型,右侧是投机解码机制。
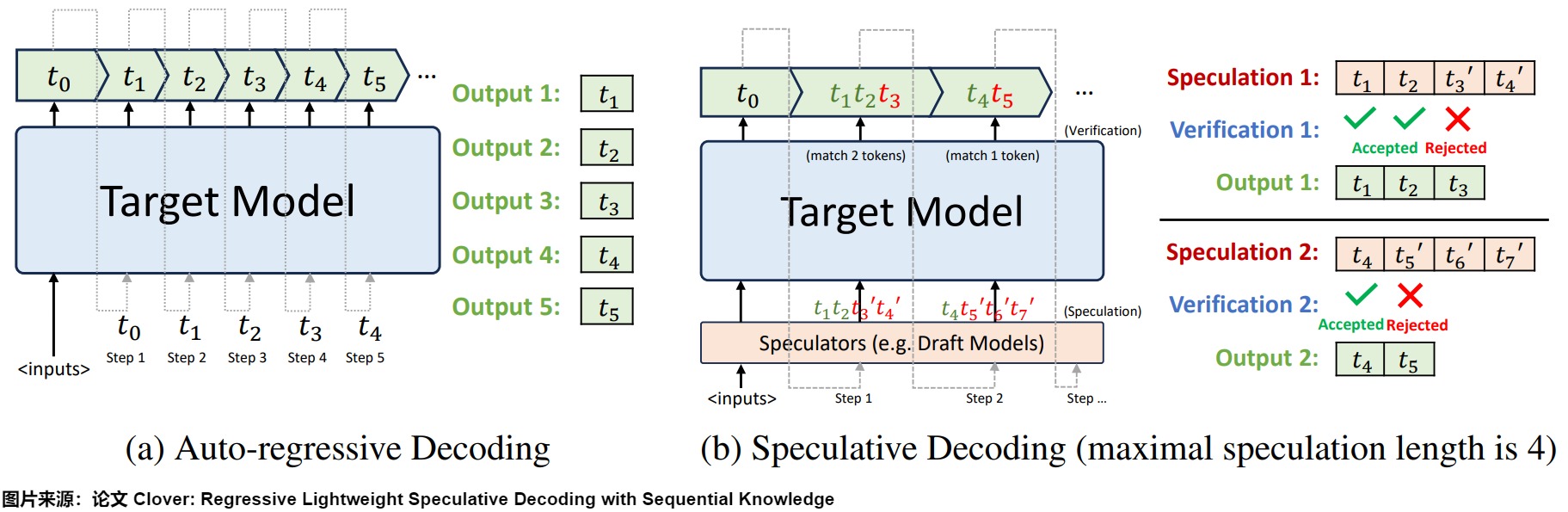
从本质上来说,投机解码希望在推理阶段在不大幅度改变模型的情况下,通过更好利用冗余算力来并行"投机"地猜测出模型接下来要输出的token。作为对比,也有一种方案是通过路由的方式组合多个不同规模和性能的模型。路由方式在调用之前已经确定好需要调用哪个模型,直到调用结束。而投机解码在一个 Query 内会反复调用大小模型。
注:
- 全部文章列表在这里,估计最终在35篇左右,后续每发一篇文章,会修改此文章列表。cnblogs 探秘Transformer系列之文章列表
- 本系列是对论文、博客和代码的学习和解读,借鉴了很多网上朋友的文章,在此表示感谢,并且会在参考中列出。因为本系列参考文章太多,可能有漏给出处的现象。如果原作者或者其它朋友发现,还请指出,我在参考文献中进行增补。
0x01 背景
1.1 问题
我们都知道,生成式 LLM 大部分是 Decoder-only 结构,其一方面模型比较大,推理时占用的存储空间、所需的计算量都比较大,另一方面,大模型解码时是一个 Token 一个 Token 串行生成,在 batch size 为 1 时,Transformer block 中的矩阵乘都退化为矩阵乘向量操作,对于 GPU 推理来说,这是非常明显的 IO bound,导致无法充分发挥 GPU 算力。
1.2 自回归解码
当前的主流 LLM 基本都是 Decoder Only 的 Transformer 模型,其推理阶段采用自回归采样,特点如下:
- 模型使用前缀作为输入,将输出结果处理+归一化成概率分布后,采样生成下一个token。
- 从生成第一个 Token之后,开始采用自回归方式一次生成一个 Token,即当前轮输出token 与历史输入 tokens 拼接,作为下一轮的输入 tokens,然后解码。
- 重复执行2。在后续执行过程中,前后两轮的输入只相差一个 token。
- 直到生成一个特殊的 Stop Token(或者满足用户的某个条件,比如超过特定长度) 才会结束。
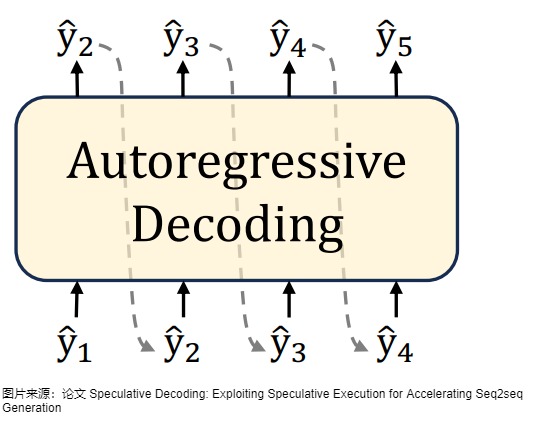
自回归解码对应的算法如下图所示。

自回归采样的缺点如下:
- 因为在生成文本时,自回归采样是逐个 token 生成的,生成下一个 token 需要依赖前面已经生成的 token,这种串行的模式导致生成速度慢,效率很低。具体参见下图。假设输出总共有 N 个 Token,则 Decoding 阶段需要执行 N-1 次 Forward,这 N-1 次 Forward 只能串行执行。
- 在生成过程中,需要关注的 Token 越来越多(每个 Token 的生成都需要和之前的 Token 进行注意力计算),计算量也会随之增大。
- 大型模型的推理过程往往受制于访存速度。因为推理下一个token的时候,需要依赖前面的结果。所以在实际使用GPU进行计算时,需要将所有模型参数以及kv-cache移至片上内存进行运算,而一般来说片上内存带宽比计算性能要低两个数量级,这就使得大模型推理是memory-bandwidth-bound的,内存访问带宽成为严重的瓶颈。
另外,大模型的能力遵循scaling law,也就是模型的参数越多其拥有的能力越强,而越大的模型自然就需要越多的计算资源。scaling law告诉我们,我们没有办法通过直接减小模型的参数量来减小访存的访问量。
为了解决推理速度慢的问题,研究人员已经进行了许多针对推理的工程优化,例如:
- 改进的计算核心实现、多卡并行计算、批处理策略等等。其中,最朴素的做法就是增大推理时的 Batch size,比如使用 dynamic batching,将多个请求合并处理,将矩阵乘向量重新变为矩阵乘操作,在 Batch size 不大的情况下,几乎可以获得 QPS 的线性提升。然而,这些方法并没有从根本上解决LLM解码过程是受制于访存带宽的问题。
- 对模型以及KV Cache进行量化,使每一个token生成过程中读取模型参数时的总比特数减小,缓解io压力。
- increasing the arithmetic intensity,即提高"浮点数计算量/数据传输量"这个比值,让数据传输不要成为瓶颈。
- reducing the number of decoding steps,即缩短解码步骤。投机解码就属于这个范畴。
0x02 定义 & 历史
2.1 投机解码
投机解码(Speculative Decoding)允许我们将在同一个用户请求内的多个 Token 一起运算。其目的和 dynamic batching 类似,也是为了将矩阵乘向量重新变为矩阵乘操作,这很适合无法获得更大 Batch size 或者只想降低端到端延时的场景。投机解码一般使用两个模型:Draft Model(草稿模型)快速生成多个候选结果,然后Target Model(目标模型)并行验证和修改,最终得到满意答案。具体而言:
- draft model用来猜测。draft model推理较快,承担了串行的工作,它以自回归的方式生成K个tokens,从而让目标模型能够并行的计算。
- target model用来评估采样结果\审核修正。target model通过并行计算多个token来从自回归模型中采样,用推理结果来决定是否使用draft model生成的这些tokens。
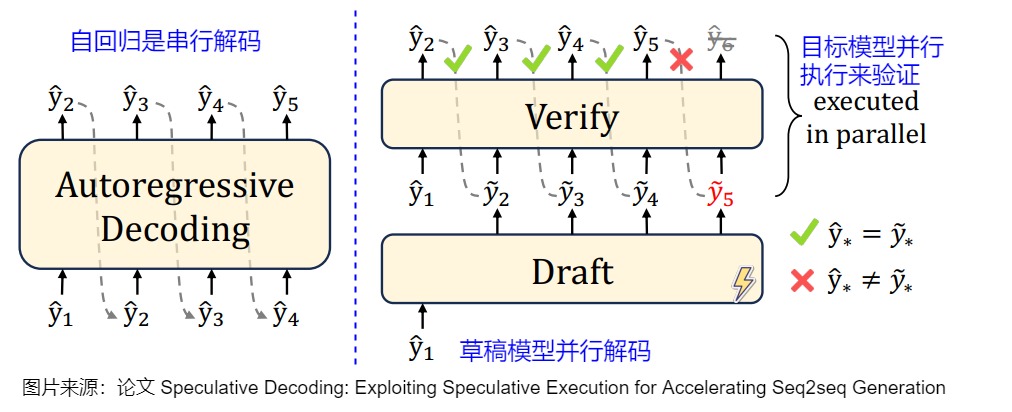
投机解码的算法如下图所示。

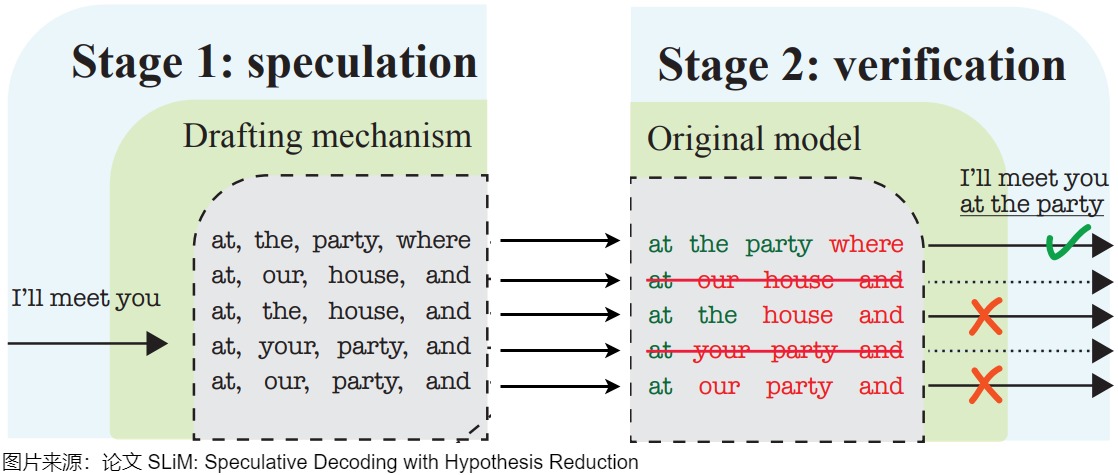
投机解码无需对输出进行任何更改,就可以保证和使用原始模型的采样分布完全相同,因此和直接用大模型解码是等价的。下图右侧,草稿模型先生成5个预测token后,将5个token一起输入给目标模型。以该前缀作为输入时,目标模型会生成若干token,然后进行验证。绿色表示草稿模型生成的token和目标模型生成的token一致,预测token通过了"验证"------这个token本来就是LLM自己会生成的结果。红色token是没有通过验证的"推测"token。第一个没有通过验证的"推测"token和其后续的"推测"token都将被丢弃。因为这个红色token不是LLM自己会生成的结果,那么前缀正确性假设就被打破,这些后续token的验证都无法保证前缀输入是"正确"的了。
2.2 发展历史
下面给出了投机解码的发展历史。
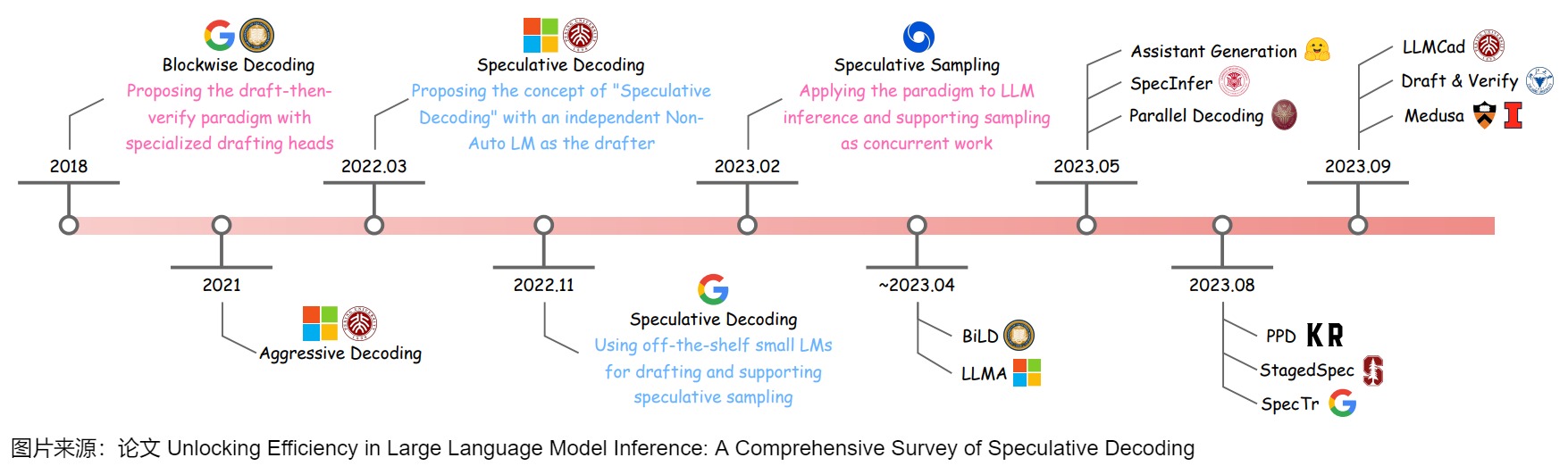
其中有两篇文章需要特殊提一下,两篇文章都算是投机解码的开山之作,其中公案我们也难以说清。
Speculative Decoding
论文"Speculative Decoding: Exploiting Speculative Execution for Accelerating Seq2seq Generation"是第一篇提出 Speculative Decoding 这个词的文章,也确立了使用 draft-then-verify 这一方法加速 Auto-Regressive 生成的范式。
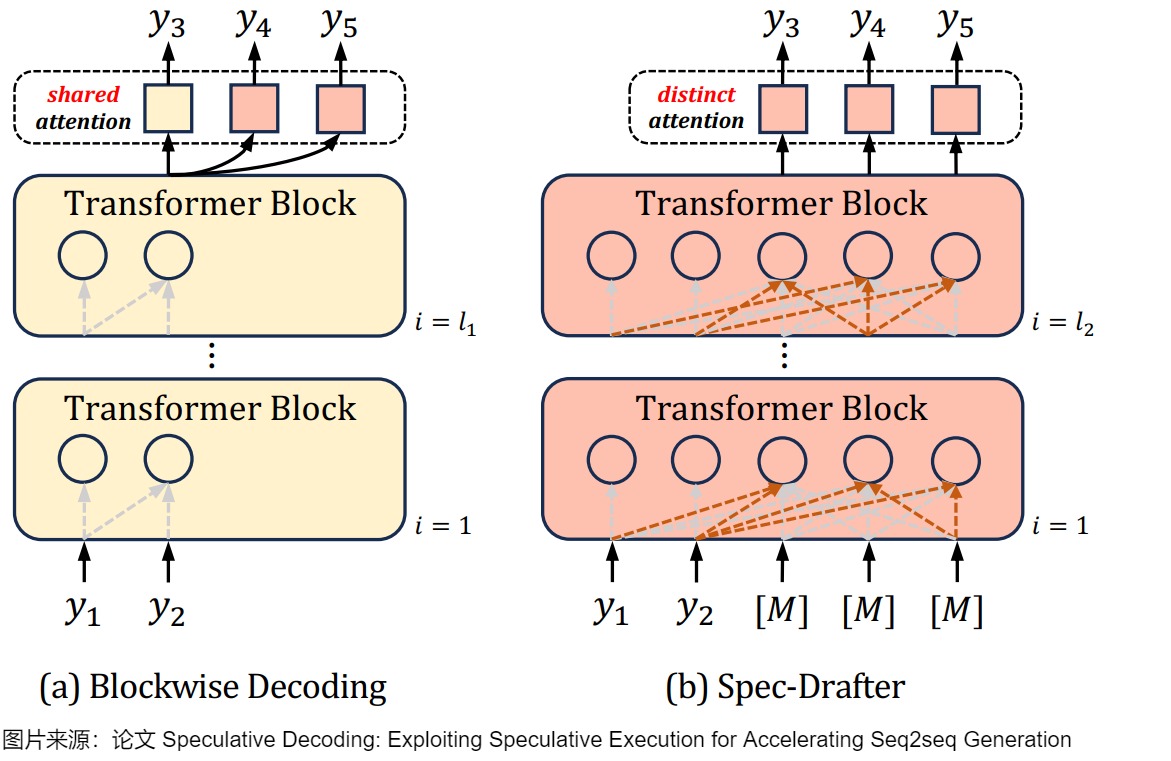
Speculative Decoding 希望解决的是现有的 Autoregressive 模型推理过慢的问题。下图(a)是Blockwise Decoding,其在目标自回归模型上引入了k − 1个FFN头,这些头使用共享注意力(shared attention)来预测下面k个tokken。(b)是Spec-Drafter模型,该模型是预测草稿token的独立模型,它使用不同的query来预测每个草稿token。下图上黄色部分是自回归AR模型,红色部分是新加入的模块。
Speculative Sampling
论文"Fast Inference from Transformers via Speculative Decoding"最早提出了 Speculative Sampling。此文章和上一篇文章是同时期的研究,被认为是SD的开山之作,后续许多研究都是基于此来展开。本文用 target model(目标模型)指代待加速的大模型,用 approximation model(近似模型)指代用来帮助加速大模型的小模型。
后续我们统一使用speculative decoding这个术语。
接下来,我们先对本领域的先驱之作"Blockwise Parallel Decoding"做简要分析,然后再结合两篇开山之作进行学习。
0x03 Blockwise Parallel Decoding
论文"Blockwise Parallel Decoding for Deep Autoregressive Models"提出的Blockwise Parallel Decoding是本领域的先行之作,或者说并行解码的第一个工作,所以我们仔细学习下,有助于我们理解后续脉络。Blockwise Parallel Decoding(BPD)使用多头的方式生成候选序列(一个串行序列),然后进行并行验证。
3.1 动机
BPD旨在解决Transfomer-based Decoder串行贪心解码的低计算效率问题:在序列生成时是串行的一个一个 Token的生成,计算量和生成结果所需的时间与生成的 Token 数目成正比。
我们接下来看看BPD的出发点和思路。
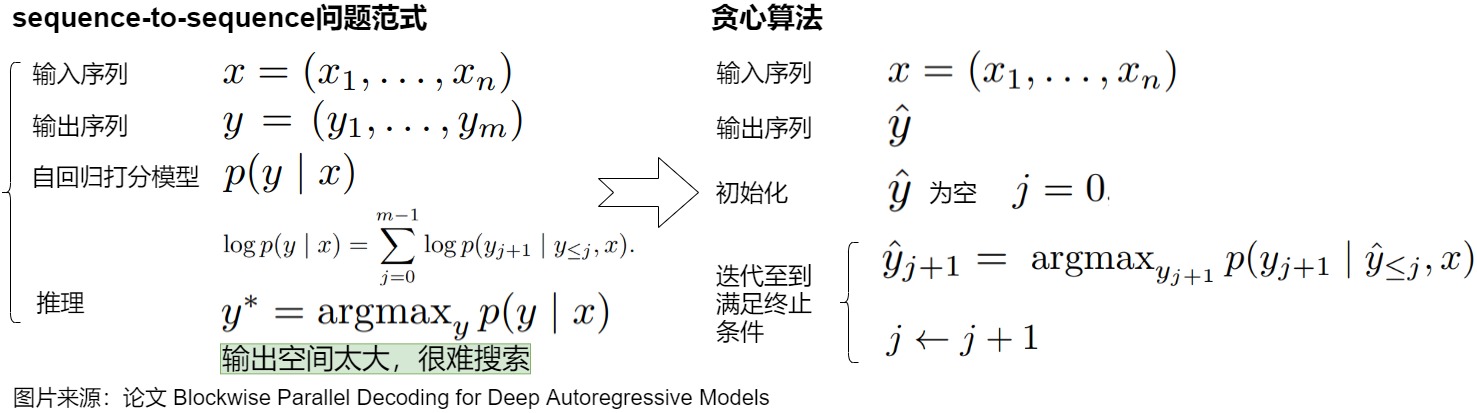
上图是贪心解码的展示。贪心解码效率很高,但可能无法找到全局最优,而且存在很多问题,具体如下。
- 假设输出序列的长度为 m,那么 Autoregressive Decoding 要执行 m 步才能获得最终结果,随着模型的增大,每一步的时延也会增大,整体时延也会放大至少 m 倍。
- 因为每次进行一个token生成的计算,需要搬运全部的模型参数和激活张量,这使解码过程严重受限于内存带宽。
为了克服上述限制,BPD的改进动机如下。
- 作者期望通过 n 步就可完成整个预测,其中 n 远小于 m。
- 但是如何打破串行解码魔咒,并行产生后k个token?因为语言模型都是预测下一个token,如果我们有k-1个辅助模型,每个模型可以根据输入序列跳跃地预测后2到k个位置的token。那么,辅助模型和原始模型就有可能独立运行,从而并行生成后k个token。
3.2 思路
论文提出了针对深度自回归模型的并行解码技术------分块并行解码(Blockwise Parallel Decoding)方案。该方案通过训练辅助模型(通过在原始模型的Decoder后面增添少量参数),使得模型能够预测未来位置的输出(并行地预测并验证后k个token),然后利用这些预测结果来跳过部分贪心解码步骤,从而加速解码过程。具体而言,BPD提出了使用特殊drafting heads的draft-then-verify范式,其三个阶段分别是Predict、Verify和Accept阶段。
- Predict 阶段使用"原模型+k-1个辅助模型"进行k个位置token的预测。论文将模型原来的单 head(最后用于预测 Token 分布的 MLP)转换为多个 head,第一个 head 为保留原始模型的 head,用于预测下一个 Token,后面新增的 head 分别预测下下一个 Token,下下下一个 Token,相当于一次预测多个 Token。
- Verify(验证)阶段使用原模型并行地验证这k个位置上候选词所形成的几种可能。因为已经生成了多个token,因此在下一次推理的时候,即可使用原模型并行地验证这些 Token 序列(由于模型计算本身是 IO bound,并行验证增加的计算几乎不会增加推理的时延)。Verify 过程会将这些token组成batch,实现合适的attention mask,一次性获得这个k个位置的词表概率。因为第一个 head 就是原始模型的 head,所以结果肯定是对的,这样就可以保证每个 decoding step 实际生成的 Token 数是 >= 1 的,以此达到降低解码次数的目的。另外,在验证同时也可顺带生成新的需要预测的 Token。
- Accept阶段会接受验证过的最长前缀,附加到原始序列上。此阶段会贪心地选择概率最大的token,如果验证结果的token和Predict阶段预测的token相同则保留。如果不同,则后面的token预测都错误。
需要说明的是,这篇论文的工作只支持贪婪解码(Greedy Decoding),不适合其他的解码算法(而Speculative Sampling可以适配Beam Search),在不牺牲效果的情况下,有效 Token 数可能并不多。而且模型还需要使用训练数据进行微调。因此,Blockwise Parallel Decoding=multi-draft model +top-1 sampling+ parallel verification。受此启发,后续提出的Speculative Sampling方法也使用小模型并行预测,大模型验证的方式解决相同的问题。
3.3 架构
BPD提出了多头并行解码机制。除了原始模型 p 外,在 Predict 阶段还有几个辅助模型 p2,...,pk 。用这些模型来辅助预测。但是我们会面临一个问题:如果这些辅助模型采用和原始模型 p 同样的结构并单独训练,那么在 Predict 阶段的计算量就是生成一个 Token 的 K 倍。即使忽略 Verify 阶段,理想情况下整个训练任务的计算量也没有降低。而且这K个模型对于内存的占用将是非常惊人的。因此,论文并没有真的构造出k-1个辅助模型,即p2,...,pk 并非是独立的原始模型的副本。论文是对原始模型略作改造,让这些辅助模型与原始模型 p1 共享 backbone,然后增加一个隐藏层,针对每个模型 p1,...,pk 都有独立的输出层。这样就就可以让新模型具备预测后k个token的能力,能保证 Predict 段实际的计算量与之前单个 Token 预测的计算量基本相当。
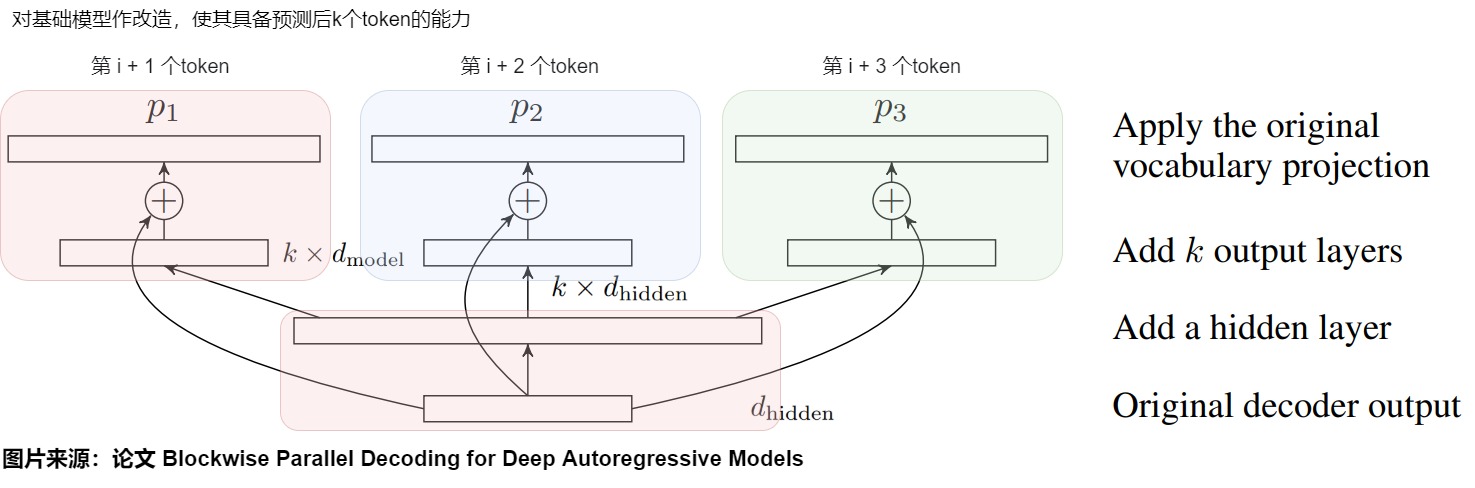
具体模型架构如下图所示,在原始模型之上一共增加了三层(从下至上):
- 在原始模型的最后一个 Transformer Decoder 层之后先加上一个隐层,它的输入是(batch_size, sequence_length, d_model),输出是(batch_size, sequence_length, k* d_model)。
- 在隐层之后会额外加上几个 head,分别为 p2,...,pk。Transformer Decoder 层输出的 logit 会先传给隐层进行投影,投影后的输出会分别传给这几个头。这些头的计算结果会分别再与原始模型的logit做残差连接。每个头负责预估一个token,这k个头的输出就是k个不同位置token的logits。头1 负责预估 next token, 头2 负责预估 next next token, 以此类推。
- 最后再将结果送入到词表投影层(包括一个线性变换和一个Softmax),预估每个词的概率分布,最终通过某种采样方法生成token。这个词表投影层是在多Head之间共享的。
主干网络 + 头1(下图红色)是原模型或者说基础模型,也就是预训练的模型。其他Head是论文说的辅助网络(auxiliary model)(蓝色和绿色分别是两个辅助网络)。既然可以根据输入序列预测下一个 Token,那么也就可以根据同样的序列预测下下一个,下下下一个 Token,只是准确率可能会低一些而已,这样就可以在 Decoding step 的同时额外生成一个候选序列,让基础模型在下次 Decoding step 来验证即可。
3.4 训练
改造后的模型还需要使用训练数据进行训练。由于训练时的内存限制,论文无法使用对应于k个project layer输出的k个交叉熵损失的平均值作为loss。而是为每个minibatch随机均匀选择其中的一个layer输出作为loss。
训练FFN的参数可以使用如下几种方式:
- Frozen Parameters:将原始模型参数冻结,只更新那些新加入的FFN层参数。这样预测下一个token肯定是准确的,但可能影响辅助模型预测的准确性。
- Finetuning:以原始参数为初始化值对全部参数进行微调,这可能会提高模型的内部一致性,但在最终性能上可能会有所损失。
- Distillation:蒸馏很适合并行解码,因为teacher和student都有相同的结构。蒸馏数据是原始模型用相同的超参数但不同的随机种子进行beam search产生的。
3.5 步骤
下图展示了blockwise decoding的三个阶段,分别是Predict、Verify和Accept阶段。
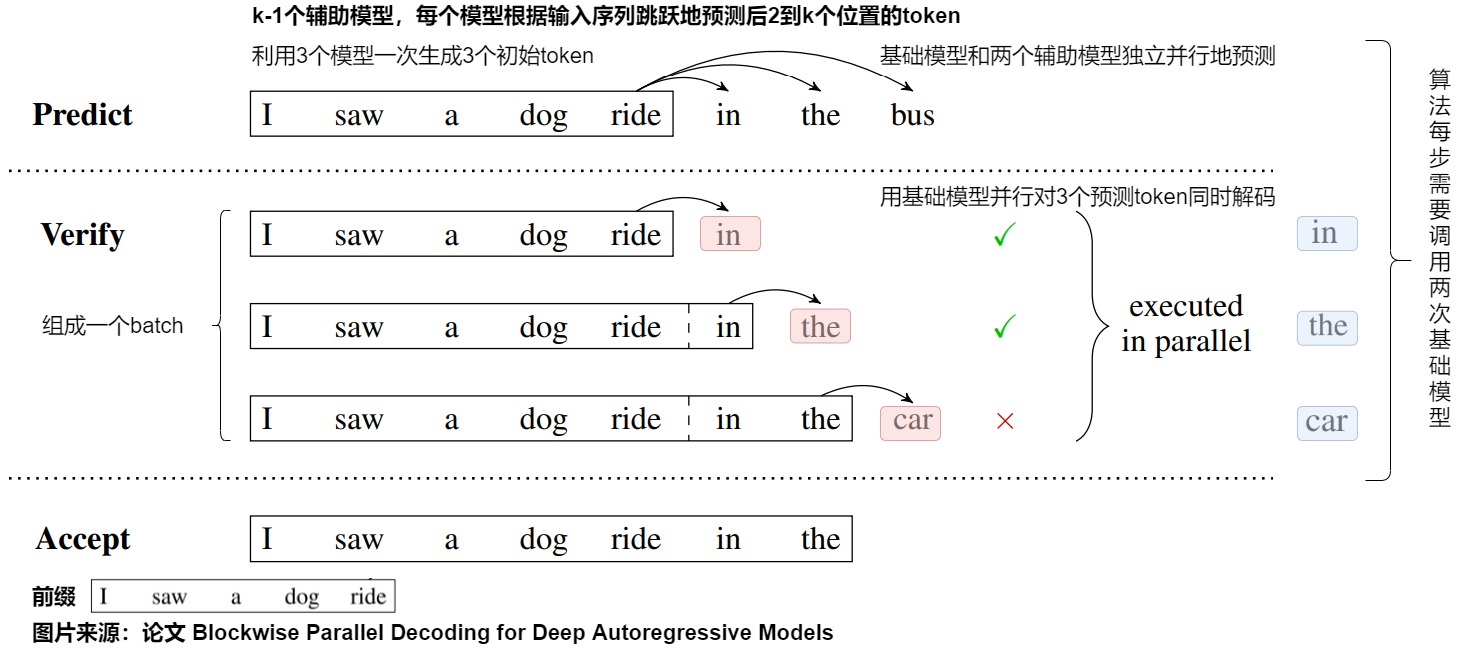
我们基于上图进行详细解读,假设要生成的序列长度为𝑚 ,并行Head数为k。
在Predict阶段中。
- 预测即使用原模型+k-1个辅助模型进行k个位置token的预测。原模型 p1 和辅助模型 p2,...,pk 都是相互独立的,可以并行的执行,因此生成这个k个单词的时间和生成一个单词时间基本一致,所以可降低整体生成的步数,也就帮助降低整体时延。
- 针对上图,则是原模型和两个辅助模型独立并行地预测出后三个token,即"in"、"the"和"bus"。
Verify阶段中,我们需要在上一步中生成的 K 个单词里选择符合要求的最长前缀。
- 将原始的序列和生成的 𝑘 个token拼接成
𝑃𝑎𝑖𝑟<𝑠𝑒𝑞𝑢𝑒𝑛𝑐𝑒_𝑖𝑛𝑝𝑢𝑡,𝑙𝑎𝑏𝑒𝑙>,这 𝑘 个𝑃𝑎𝑖𝑟<𝑠𝑒𝑞𝑢𝑒𝑛𝑐𝑒_𝑖𝑛𝑝𝑢𝑡,𝑙𝑎𝑏𝑒𝑙>将组成一个Batch(也会加上对应的掩码),一次性发给头1并行地验证这k个位置(看看头1生成的token是否跟 𝑙𝑎𝑏𝑒𝑙 一致)。 - 针对上图,则是对上一步生成的三个token进行打分。具体而言,我们把生成的'in the bus'和前缀拼接后送入原始模型进行一次前向推理运算,上图Verify阶段中的黑框里是 𝑠𝑒𝑞𝑢𝑒𝑛𝑐𝑒_𝑖𝑛𝑝𝑢𝑡 ,蓝色的是要验证的 𝑙𝑎𝑏𝑒𝑙 ,箭头指向的红色是预测结果。这样只进行一次前向推理运算,就可以获得后三个输出位置词表的概率分布。
- batch的第一个输入是"I saw a dong ride",输出是"in"。
- batch的第二个输入是"I saw a dong ride in",输出是"the"。
- batch的第三个输入是"I saw a dong ride in the",输出是"car"。
在Accept阶段中会选择 𝐻𝑒𝑎𝑑1 预估结果与 𝑙𝑎𝑏𝑒𝑙 一致的最长的 𝑘 个token,作为可接受的结果。
- 我们可以贪心地选择概率最大的token作为验证结果。从左到右看,如果验证结果的token和Predict阶段预测的token相同,则保留这个token。如果不同,则该token和其之后的token预测都错误。
- 因为只接受第一个不一致的单词之前的单词,并且验证时候使用的就是原始模型 p1 ,这也就保证了最终结果是与原始序列预测的结果是完全一致的。
- 针对上图,因为"car"和"bus"不一致,所以只保留"in"和"the"。
假设要生成的序列长度为𝑚 ,并行Head数为𝑘。自回归生成方法中,总共需要 m 步执行。BDP中,对每 𝑘 个token执行一次上述三阶段过程,predict阶段执行1步产出多个Head的输出, verify阶段并行执行1步,accept阶段不耗时。因此在理想情况下(每次生成的 K 个 Token 都能接受),总的解码次数从 m 降低到 2m/K。这其中由于 Predict 阶段 p1 和 Verify 阶段都使用的原始模型,所以只使用两次原模型。
3.6 优化
由于存在 Predict 和 Verify 两个阶段,因此即使理想情况下整体的解码次数也是 2m/K,而不是最理想的 m/K。事实上,由于 Predict 阶段的模型有共同的 backbone,并且 Verify 阶段使用的模型也是原始模型 p1,因此就可以利用第 n 步的 Verify 结果来直接生成第 n+1 步的 Predict 结果。于是作者们进一步优化这个算法,在原始模型验证时同时预测后k个token。这样Predict和Verify阶段可以合并,验证同时也获得了后k个token的候选。
优化之后,模型第一次推理只执行predict阶段( 1 步),调用一次原始模型。然后进入verify和predict重叠的阶段,每次处理序列往前走 𝑘 长度,直到生成终止token(共m/k步,调用m/k次原始模型)。即,除了第一次迭代,每次迭代只需调用一次模型forward,而不是两次,从而将解码所需的模型调用次数减半。进一步将模型调用次数从2m/k减少到m/k + 1。
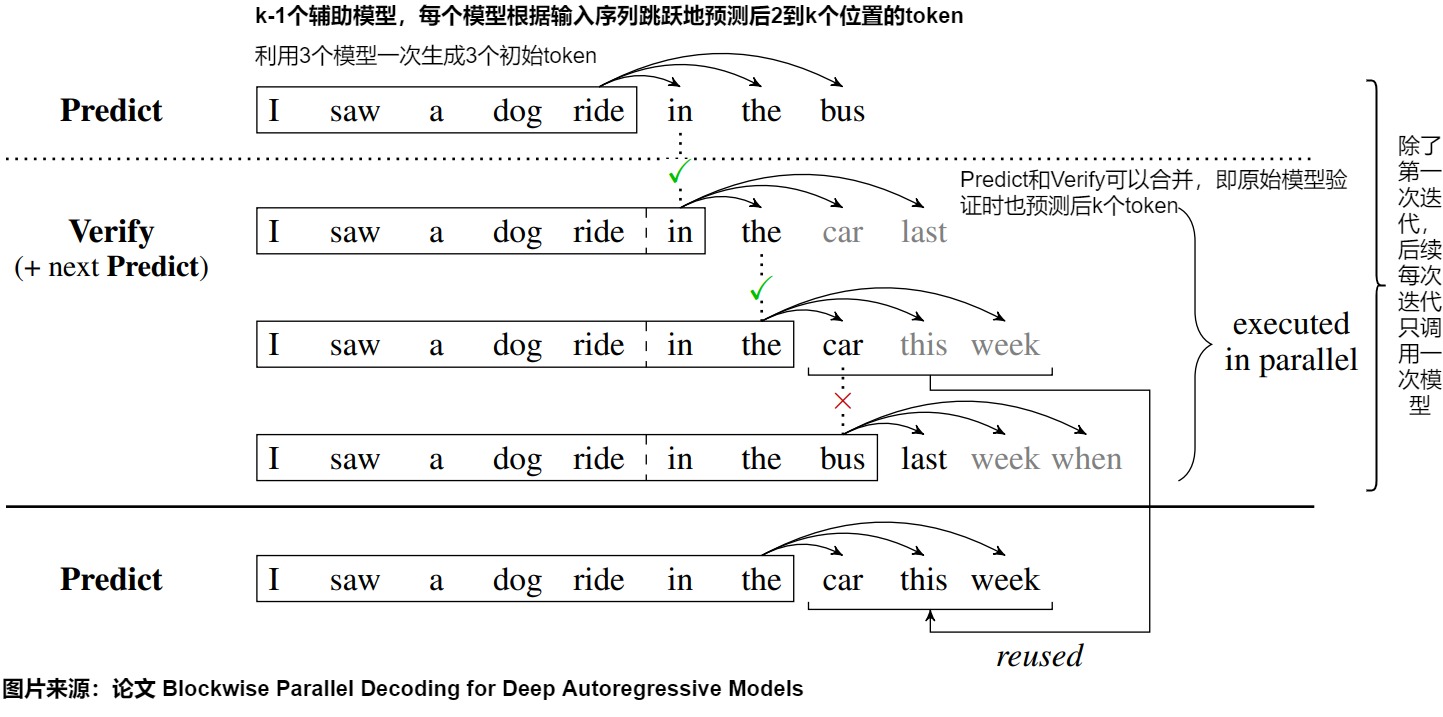
如上图所示,还是以之前的例子为例:
-
Predict 阶段,输入单词 I saw a dog ride in the,进行一次原模型推理,生成了新单词 in,the,bus。
-
Verify 阶段:
- 第一组:输入 I saw a dog ride,待验证单词为 in,实际预测得到 in,the,car,last,第一个单词的 Top1 为 in,结果相同,接受 in 这个单词
- 第二组:输入 I saw a dog ride in,待验证单词为 the,实际预测得到 the,car,this,week,第一个单词的 Top1 为 the,结果相同,接受 the 这个单词
- 第三组:输入 I saw a dog ride in the,待验证单词为 car,实际预测得到 bus,last,week,when,第一个单词的 Top1 为 bus,结果不相同,不接受 car 这个单词。
-
Accept 阶段。因为第三组的 bus 和 car 不相同,所以不接受第三组的结果,接受第二组的结果。因此可以把 car,this,week 作为新的 Predict 结果,继续进行 Verify。
3.7 收益
我们接下来看看收益。
这种方案之所以可以加速解码,在于Verify阶段可以用基础模型 p1 并行对k个预测token进行同时解码。因为每个迭代Predict阶段产生k个token可以看成一个block,故这种方法被称为blockwise parallel decoding。这种方法推理时得到的结果和自回归方式解码的结果一样,因此没有任何生成效果的精度损失。
Blockwise Decoding的速度取决于执行模型forward的次数。在访存受限的情况下,对"I saw a dog ride"进行forward运算的时间和对"I saw a dog ride in the car"进行forward运算的时间近似相同,因为它们都需要访问模型参数和KV Cache,多出几个tokens带来的激活访存开销显得微不足道。
0x04 原理
看完了BPD这个基础之作,我们再来看看投机解码。
4.1 动机
投机解码的动机来自几点观察和一个借鉴。
4.1.1 观察
我们首先看看几点关键观察结果:
- 困难任务包含容易子任务。在困难的语言建模任务中,通常包含了一些相对容易的子任务,比如,预测有些token时,softmax输出的概率分布会集中在某些token上,这说明模型有较大的置信度确定下一个输出的token。这意味着不是所有的解码步骤都同样困难,如果我们用小模型去回答这些简单的问题,在遇到难题的情况下再调用大模型,就可以提高整体的生成效率。即,大多数容易生成的tokens其实用更少参数的模型也可以生成。
- 内存带宽和通信是大模型推理的瓶颈。对于 LLM 推理来说,通常瓶颈不是数学计算,而是内存带宽及通信量、通讯速度。LLM每个解码步所用的推理时间大部分并不是用于模型的前向计算,而是消耗在了将LLM巨量的参数从GPU显存(High-Bandwidth Memory,HBM)迁移到高速缓存(cache)上(以进行运算操作)。这意味着在某些情况下,适当增加计算量并不会影响推理速度,可以用于提高并发性。
- 大模型在做推理任务(decoding阶段)时,往往batch size为1,一次只能生成一个token,无法并行计算,导致大量算力冗余。事实上,在数量增加有限的情况下,输入多个tokens和输入一个token单轮的计算时延基本一致。如果我们能让大模型一次处理一批tokens,就能利用上算力,让大模型达到计算和访存平衡。
4.1.2 借鉴
"Speculative execution"(猜测性执行)是一种在处理器(CPU)中常见的优化技术。
它的基本思想是在不确定某个任务是否真正需要执行时,提前执行该任务,然后再来验证被执行任务是否真的被需要,这样做的好处可以增加并发性和性能,一个典型的例子是分支预测(branch prediction)。在处理器中,"speculative execution"通常用于处理分支(branch)指令。当处理器遇到一个分支指令时,它不知道分支条件的具体结果,因此会选择一条路径来执行。如果分支条件最终符合预期,那么一切正常,程序将继续执行。但如果条件不符合,处理器会回滚到分支前的状态,丢弃之前的操作,然后选择正确的路径进行执行。
4.2 思路
上文提到,投机解码最早在两篇论文中被提出。基于上述的观察结果和Speculative execution的机制,在解码自回归模型方面,两篇论文的作者将"speculative execution"这一优化技术进行了推广,将其应用于自回归模型的解码过程中。
投机解码使用两个模型:一个是原始target model(目标模型),另一个是比原始模型小得多的draft model(近似模型/草稿模型)。draft model和target mode联合推理,draft模型生成γ个token,而target模型则去验证γ个token是否为最后需要的token。就是使用一个小模型来生成多个草稿token,然后使用大模型对这多个草稿token做并行验证、纠正和优化。这样就可以在接近大参数模型的生成一个token的时间里面生成多个tokens。我们来做具体分析。
- "投机解码"指的是用小模型的输出去投机。
- 先用更高效的近似小模型预测后续的若干个tokens(一些可能的推理结果,这些结果被称为"speculative prefixes"),这充分利用了小模型decoding速度快的优点。
- 解码过程中,某些token的解码相对容易,某些token的解码则很困难。因此,简单的token生成可以交给小型模型处理,这些小模型应该也可以获取正确的预测结果。而困难的token则交给大型模型处理。如果当前的问题比较简单,则小模型有更大的可能猜对多个token。
- 论文里的并行就是指大模型一次计算多个token,节省下来传输损耗。即用大模型并行验证这一些token是否符合大模型的输出,其思路如下。
- 在一次前向传播中,同时验证多个 draft token。在第一个 draft token 与原始模型输出不相符的位置截断,并丢弃在此之后的所有 draft token。这就是"Speculative execution"中的丢弃。
- 利用prefill阶段比decoding阶段计算效率高的特点。大模型可以一次prefill输入几个小模型decode步结果来仲裁、提高推理速度。用大模型的prefill模式代替decode模式可以节约大模型的访存,以及充分利用tensor core来加速矩阵乘法。这不是一个纯算法或者纯硬件系统角度考虑问题的加速方案,而是一个同时从考虑算法以及硬件系统的解决方案。
- 然后,利用一种新颖的采样方法(speculative sampling)来最大化这些推测性任务被接受的概率。"speculative decoding"这种验证和重采样过程在理论上是等价于直接从目标 LLM 采样,因此,可以保证最终生成的文本分布与目标 LLM 一致。
总结下,"speculative decoding"可以通过充分利用模型之间的复杂度差异,以及采用并行计算的方法,使得从大型自回归模型中进行推理变得更快速和高效。同时保持了与目标模型相同的输出分布(在实现对target LLM推理加速的同时,不损失LLM的解码质量),而无需更改模型架构、训练过程或输出。下图给出了执行流程。
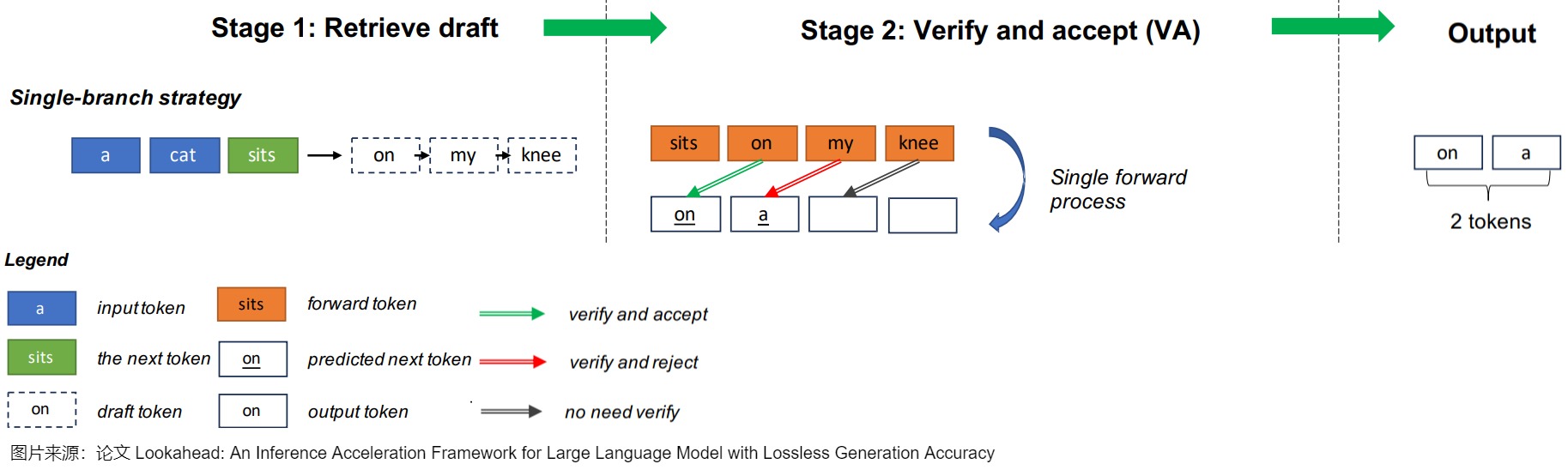
4.3 对比
投机执行和投机解码对比如下。
| 类别 | 投机执行 | 投机解码 |
|---|---|---|
| 提前执行 | 遇到一个分支指令时,CPU不知道分支条件的具体结果,因此会选择一条路径来执行 | draft model串行推理,生成草稿token。相当于用draft model做逐个token的decoding |
| 验证 | 验证执行结果 | target model针对draft model的串行产生结果并行推理,做验证和优化。相当于用大模型一次prefill输入小模型的几个decode步结果来仲裁 |
| 验证成功 | 如果分支条件最终符合预期,那么一切正常,程序将继续执行 | 接受小模型产生的token |
| 验证失败 | 如果条件不符合,处理器会回滚到分支前的状态,丢弃之前的操作 | 在第一个 draft token 与target model输出不相符的位置截断,并丢弃在此之后的所有 draft token |
| 失败后修复 | 选择正确的路径进行执行 | 调整概率分布 |
投机解码和之前方法对比如下。
| 类别 | 之前方案 | 投机解码 |
|---|---|---|
| 是否改变模型架构 | 许多先前的方法需要修改模型的结构,以使推理过程更高效 | 不需要 |
| 是否改变训练程序 | 一些方法可能需要修改训练过程,以便模型在推理阶段能够更有效地运行 | 不需要修改训练过程,可在现有模型上直接应用 |
| 是否重新训练 | 先前的方法可能需要对模型进行重新训练,以适应新的架构或训练程序 | 不需要 |
| 是否改变输出分布 | 先前的方法在加速推理过程时可能会导致模型的输出分布发生变化 | 通过"speculative sampling"方法,保证了从模型中生成的结果具有与原始模型相同的分布 |
另外,块并行解码(blockwise parallel decodin)和推测解码之间的主要区别在于它们的模型使用。投机解码需要额外的小模型来自回归地生成speculative tokens。这些小型模型受到约束,比目标模型更有效,因此加速可以覆盖它们的成本。
总的来说,作者提出的方法在加速推理过程时避免了许多先前方法所涉及的模型结构和训练方面的变化,同时保持了相同的输出特性。
4.4 分类&设计
投机解码实现加速的关键主要在于如下两点:
- "推测"的高效性和准确性:如何又快又准地"推测"LLM未来多个解码步的生成结果。
- "验证"策略的选择:如何在确保质量的同时,让尽可能多的"推测"token通过验证,提高解码并行性。
因此,研究人员通常基于这两点来对投机解码的实现和研究进行分类。当然,其分类方式也会略有差别。下图是论文"Unlocking Efficiency in Large Language Model Inference: A Comprehensive Survey of Speculative Decoding"给出的投机解码技术的一个正式分类,包括:
- draft model的策略。具体涵盖如何设计模型,运行终止条件,如何管理多个模型(如果有)。"推测"阶段的设计聚焦在"推测精度(accuracy)"和"推测耗时(latency)"的权衡上。一般来说,用以推测的模型越大,推测精度越高(即通过验证的token越多),但是推测阶段的耗时越大。如何在这两者之间达到权衡,使得推测解码总的加速比较高,是推测阶段主要关注的问题。
- 验证策略。此类别涉及到验证方案和验收标准的设计。验证模型通常是目标模型,其首要目的是保证解码结果的质量。接受标准旨在判断草稿token是否应(部分)接受,即接受的token长度是否小于k。在每个解码步骤中,验证模型会并行验证草稿token,以确保输出与目标LLM对齐。此过程还决定了每一步接受的token数量,这是影响加速的一个重要因素。采样方法具体来说也分为无损采样和有损采样。(a)无损采样主要是说对于原始LLM来说仍然采用原先的采样方法比如贪婪采样或者温度采样等等,然后对应地检查draft中是否有符合要求的token。这种方法核心就是drafting对于原始LLM来说完全透明,不会损失模型性能。(b)有损采样主要是说通过校验阶段对draft质量的评估,然后根据一些先验的阈值来筛选一些高质量的draft接受,这种方法的核心就是为了提高draft的接受率,在可接受的一些质量损失情况下获得更高的加速。常见验证标准包括Greedy Decoding,Speculative Sampling,Token Tree Verification等。因为,并不是所有概率最大的token都是最合适的解码结果,所以也有一些工作提出可以适当地放松"验证"要求,使得更多高质量的"推测"token被接受,进一步提升加速比。
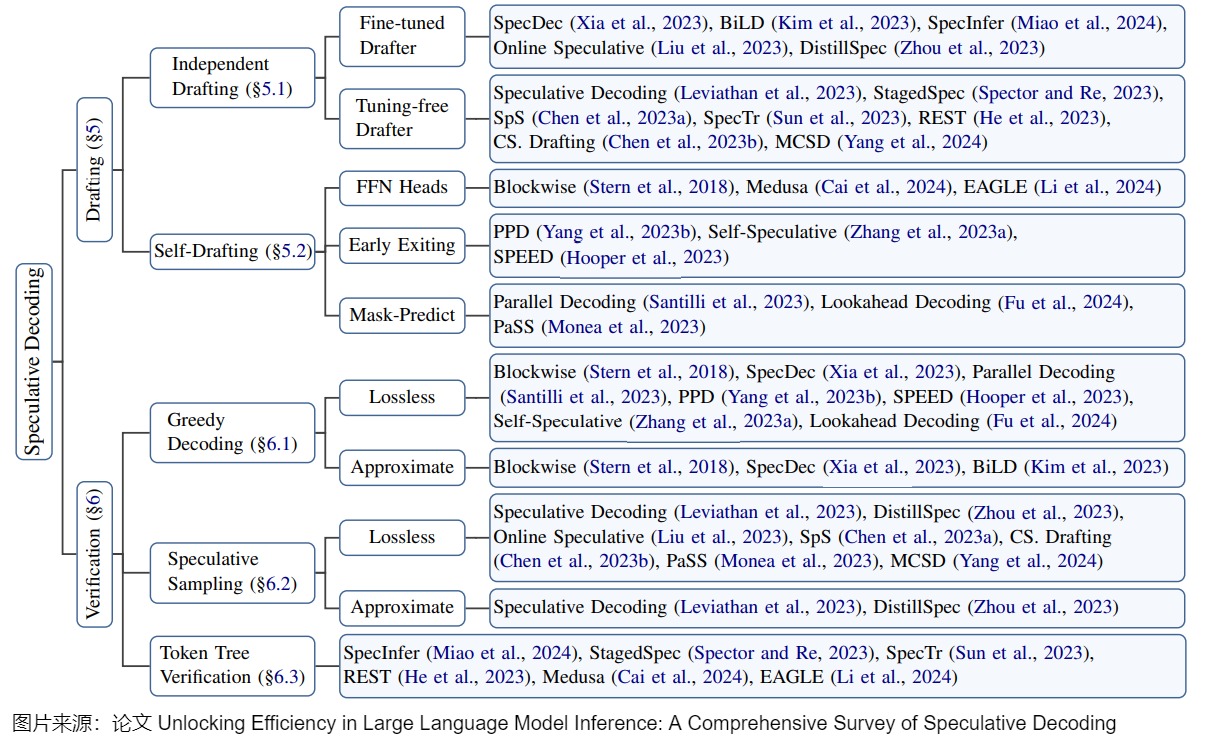
下图则是该论文中对分类内容的进一步细化。draft model的策略对应下图标号1。验证策略对应下图标号2。具体的投机解码方法则对应下图标号3。
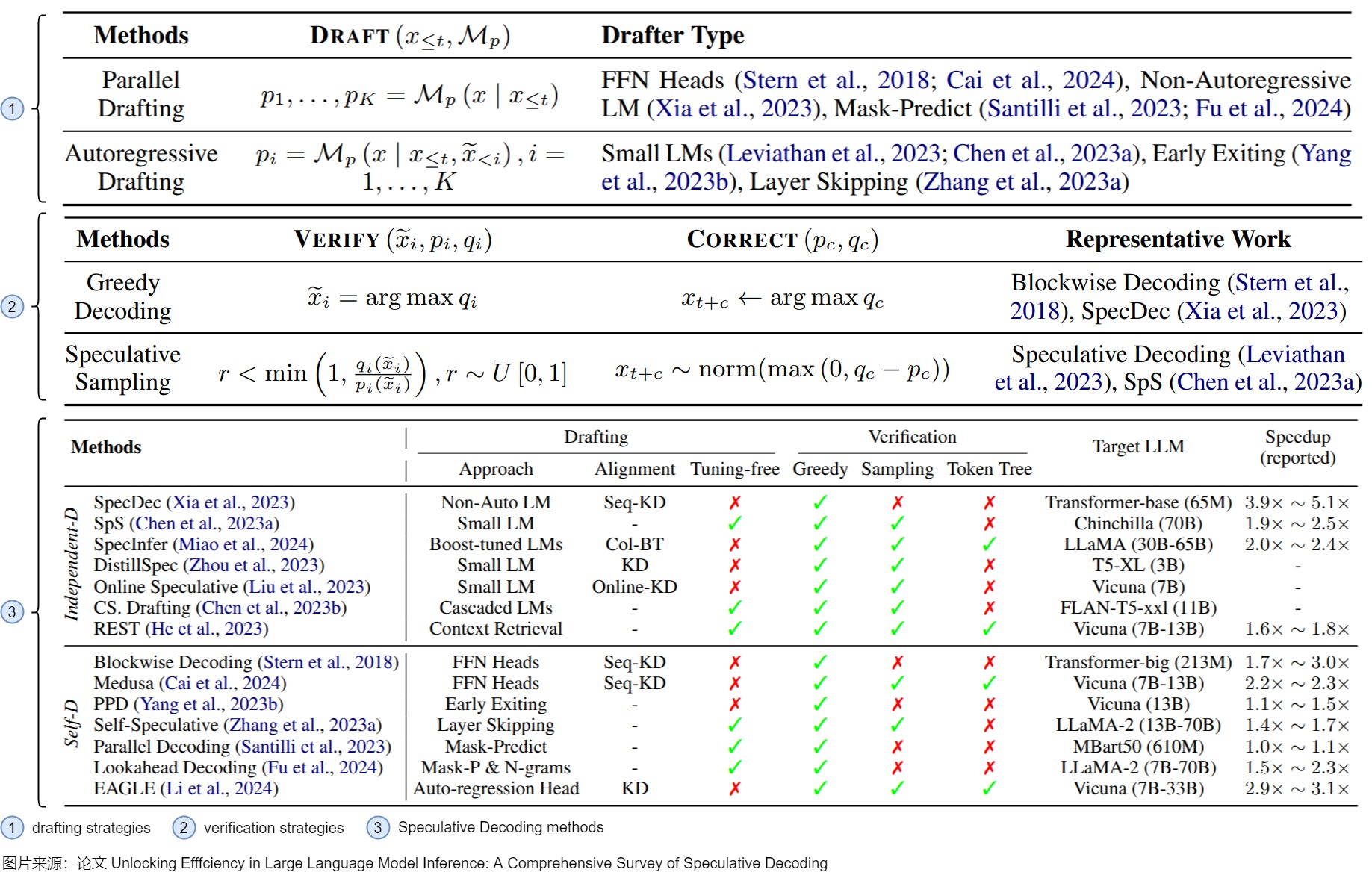
4.4.1 推测阶段的策略
推测阶段的策略主要有如下几个部分。
产生草稿
在某种程度上,草稿模型本身通常是一个因果语言模型,可以生成推测性的标记。草稿模型可以是目标模型之外的一个额外的小模型,如 speculative decoding 中生成候选token,也可以是连接到目标模型的几个轻量级预测头,如blockwise parallel decoding中预测即将到来的token。最近的进展表明,草稿模型也可以是从大型语料库中检索标记的检索者(retriever),以完成前面的上下文。
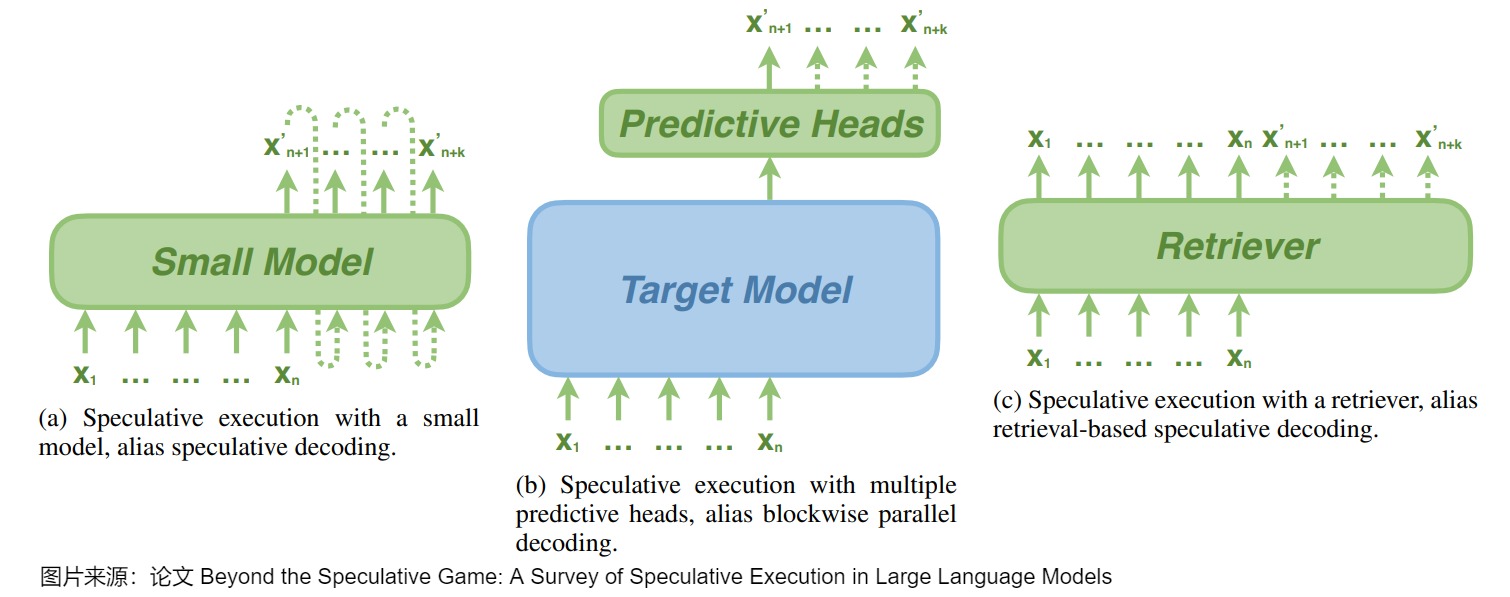
这些草稿模型具体特点如下。
- Independent Drafting。主要思路是:拿一个跟target LLM同系列的smaller LM进行"推测"。因为是同系列的模型,所以该小模型本身就存在一定的和target LLM之间的"行为相似性"(behavior alignment),适合用来作为高效的"推测"模型。需要强调的是,小模型必须与目标模型具有完全相同的词表。目前对于该思路的优化主要集中在增强小模型和大模型之间的"行为相似性"(behavior alignment),让小模型模仿得"更像"一些。比如知识蒸馏。这种方案的优点是易于实践和部署。缺点是:并不是所有的LLM都能找到现成的小模型;在单个系统中集成两个不同的模型会引入额外的计算复杂性,尤其不利于分布式部署场景;而且往往需要从头开始训练一个草稿模型,此预训练过程需要大量额外的计算资源。此外,单独的预训练可能会在草稿模型和原始模型之间产生分布变化,从而导致原始模型可能不喜欢的序列结果。
- Self-Drafting。因为上述劣势,相关研究工作提出利target LLM自己进行"高效推测",即使用验证模型本身的作为drafting model,比如,重用在原始LLM中的一些中间结果或者参数,用隐藏层状态来更好地预测未来序列。这种方式天然就没有模型表现一致方面的问题,减少了额外的计算开销,对分布式推理也很友好。在时延方面,Self-Drafting使用一些策略来使得验证模型平均参数量减少,以此来达到高效的目的。比如Blockwise Decoding和Medusa在target LLM最后一层decoder layer之上引入了多个额外的FFN Heads,使得模型可以在每个解码步并行生成多个token,作为"推测"结果。然而,这些FFN Heads依然需要进行额外的训练。除了这两个工作,还有一些研究提出利用Early-Existing或者Layer-Skipping来进行"高效推测",甚至仅仅是在模型输入的最后插入多个[PAD] token,从而实现并行的"推测"。Early-Existing则是基于saturation的观察:在生成某个token时,如果在经过第
i层的前后输出token完全一致,我们就认为已经达到饱和点,后续层不需要再继续处理,直接返回第 i 层生成的 token即可。因为除去了第i层后面的层,所以模型参数量会减少。Layer-Skipping是判别哪些token如果被跳过,但是对大多数token生成影响不大,就在生成token时跳过这些层,以此减少drafting model的参数量。 - 基于检索的方法。其思想是大部分常见的句子里面的单词组是可以统计出来的,因此在生成某个token之后,可以通过这个token去检索统计的数据库得到这个token之后大概率是哪些tokens,然后把这些tokens取出来去做验证。
此外,草稿模型不仅限于一个小模型。有人认为,在集成学习的推动下,不同尺度的分阶段或级联小模型可以进一步提高性能。比如论文"Cascade Speculative Drafting for Even Faster LLM Inference"提出了Vertical Cascade 和 Horizontal Cascade。Vertical Cascade 用 Speculative Decoding 来加速 Speculative Decoding。Horizontal Cascade 指的是在接受率较高的前几个 token 用较大的 Draft Model,在接受率较小的靠后的 token 用较小的模型来"糊弄"。
终止条件
speculative tokens的序列太短或太长都是次优的,但是也难以找到非常合适的判别标准。因此,研究人员也对终止条件进行了深入研究,具体大致分为几种。
- Static Setting:最简单的解决方案是将长度k设置为一个静态值,该值可以迭代和手动重新设置。
- Adaptive Thresholding:虽然静态设置可以满足大多数用例,但需要不停的手动调节也可能很麻烦。为了解决这个问题,已经提出了自适应阈值方法,旨在尽早停止基于每个token一致性(per-token conffdence)的草稿生成动作。如果一致性低于阈值,草稿模型的生成动作将停止。阈值可以根据某些优化目标(例如,草稿token的质量)进行自适应调整。
- Heuristic Rules:一些启发式规则也可以用于终止条件的判断。比如,如果验证中完全接受之前的猜测,则推测token的长度将增加,否则将减少。另一种方法可能是从系统服务的角度根据批量大小来改变长度。
尽管已经开发了各种方法来自动检测终止条件的理想值,但仍然很难判断它们是否足够好。在这种需求下,我们应该建立更稳健的方法来搜索和设置这些参数,从而获得更稳定、更吸引人的性能。
4.4.2 验证阶段的策略
在verification阶段,也就是使用大模型校验阶段中,分为验证方案(如何组织多个序列的输入,比如token树验证(token tree verification))和验收标准的设计(采样方法,比如贪婪采样,nucleus 采样,typical 采样)。
验证方案
组织多个序列的输入最简单的方法就是直接将所有可能输入形成多个batch。
如果只需要验证一个token,那么基于链的验证器(将token作为序列或链接收的通用验证器)应该就足够了。但是,如果使用多个token,逐一连续验证这些token会有冗余计算的问题,将过于耗时。比如有两个序列"maching learning is a"和"machine learning is the",其实区别只在于最后一个token 是"a"还是"the",前缀相同。
因此,有研究人员提出了一种基于树的验证方法,该策略使目标LLM能够并行验证多个草稿序列。该方法首先通过共享前缀从多个候选token序列建立一个trie,并从trie树中修剪不太频繁的节点。然后,它在一次运行中用树注意力对其进行并行验证(即,子token只能通过注意力掩码看到其父token),这促进了对潜在多token的并行验证。作为对比,如果是单个token,只需要一个注意力链。而基于树的验证方法所依赖的是因果关系和下三角关系(causal and lower-triangular)掩码,如下图所示。
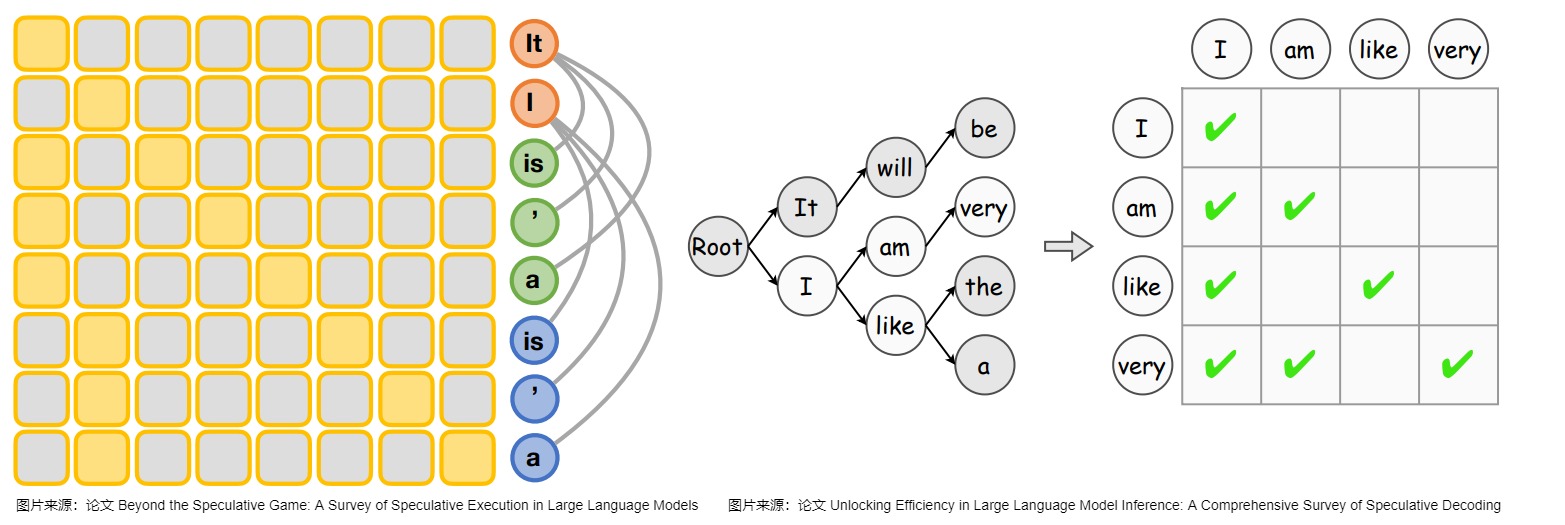
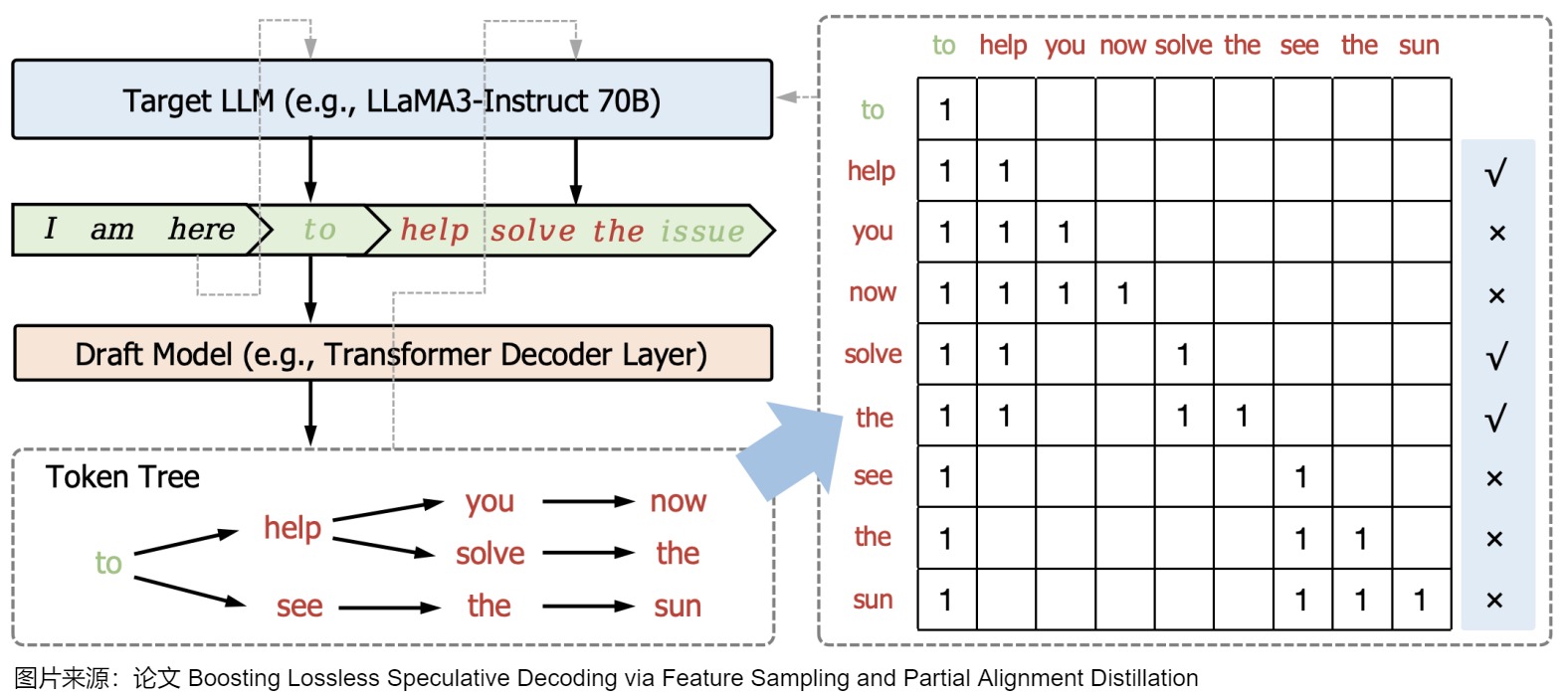
验收标准
一旦草稿token被输入目标模型,我们就可以获得相应的输出概率。通过对齐推测token和概率,我们可以推断每个token在草稿中是否有效。
精确匹配
最简单的接受标准是精确匹配,它检查speculative token是否相应地具有最大概率。该策略是基于贪心算法的。贪心采样的验证主要是保证Drafting model和Verification model都使用贪心策略的时候结果一致。也就是说,需要验证验证模型的每一个生成是否和drafting model的生成完全一样。
注意:两篇开山之作的\(M_p\),\(M_q\)是相反的,请大家在阅读时候务必注意。

虽然精确匹配简单清晰直接,可以用较小的成本来保证经过验证的输出与目标模型本身的输出一致,但是存在一些问题:
- 虽然精确匹配可以用较小的成本来保证经过验证的输出与目标模型本身的输出一致,但只有在使用贪婪解码时,这种等式才成立。
- 对于目标模型使用采样解码(sampling decoding)的情况,精确匹配很难从草稿模型中接受token,这可能会导致解码速度减慢而不是加快。
- 过于严格的匹配要求通常会导致拒绝高质量的token,仅仅是因为它们与目标LLM的前1个预测不同,从而限制了范式的加速。
拒绝采样(Rejection Sampling)
基于上述问题,多项研究提出了各种近似验证标准。与无损标准相比,这些方法略微放宽了匹配要求,以更加信任草稿,从而提高了草稿token的接受度。比如,研究人员提出了一种从拒绝采样(Rejection Sampling)中修改的验收标准来缓解这一问题(就是那两篇开山之作)。理论上,这种接受标准可以应用于贪婪解码和采样解码。

Typical Acceptance
上述两个验收标准为质量提供了严格的保证。然而,过于严格的验收标准可能会抵消并行验证的努力,并降低推测执行的负担,尤其是在施加温度参数的情况下。因此,在某些情况下,需要适度放宽接受标准,以实现更明显的加速。Typical Acceptance就可以做到这一点:如果token的投机概率超过硬阈值,则接受草稿中的token。另外,阈值也是可以通过top-k约束动态调整的。对于提供多个token的情况,Typical Acceptance将考虑形成最长序列的token,并放弃其他token。
0x05 算法
5.1 总体流程
下图给出了投机解码的算法总体流程。该算法通过首先使用更高效的近似模型 \(M_q\) 生成多个猜测token,然后使用目标模型 \(M_p\)并行评估这些猜测token的概率,并根据评估结果来决定哪些猜测token可以被接受(并行地接受那些能够导致相同分布的猜测token)。如果需要,算法还会调整目标模型的分布以保持一致性。最终,算法会返回从 \(M_p\)和 \(M_q\)中得到的生成结果。这个过程有效地利用了两个模型的优势,加速了生成过程。
这里假设\(p_i(x)\),\(q_i(x)\)分别是target,draft模型的分布。

我们用一个例子展示随机采样的工作方式。下图中,每一行代表一次迭代。绿色的token是由近似模型提出、且目标模型接受的建议。红色token:近似模型提出但目标模型拒绝的建议;蓝色token:目标模型对于红色token的订正,即拒绝红色的token并重新采样得到蓝色的token。
在第一行中,近似模型生成了5个token,目标模型使用这5个token和前缀拼接后的句子"[START] japan's bechmark bond"作为输入,通过一次推理执行来验证小模型的生成效果。因为最后一个token "bond"被目标模型拒绝,重新采样生成"n"。这样中间的四个tokens,"japan" "'s" "benchmark"都是小模型生成的。以此类推,由于用大模型对输入序列并行地执行,大模型只forward了9次,就生成了37个tokens。尽管大模型的总计算量不变,但是大模型推理一个token的延迟和小模型生成5个token延迟类似(并行总是比一个一个生成要快),从而显著提高了生成速度。

5.2 关键步骤
我们接下来分析SpeculativeDecodingStep算法的关键步骤和操作。
5.2.1 前置条件
算法的输入有三个参数:目标模型(target model)\(M_p\),草稿模型(draft model)\(M_q\)和已知前缀prefix。
target model
- 目标模型是指原始的大型自回归模型,例如大型的Transformer模型。它是进行推理的主要模型,负责生成精确的输出。目标模型通常拥有更多的参数和计算资源,但也因此导致单步推理速度较慢。
- 假设 \(M_p\) 为目标模型,模型推理就是给定前缀输入 x<t,从模型获得对应的分布 p(xt|x<t)。投机解码要做的就是加速这个推理过程。
draft model
- 草稿模型是一个更为高效的近似模型,其设计旨在在给定前缀的情况下,能够更快地生成下一个token。相对于目标模型,它可能具有较少的参数和更高的计算效率,以便提高整体推理速度。草稿模型可以采用与原始模型相同的结构,但参数更少,或者干脆使用n-gram模型。
- 假设 \(M_q\) 为针对相同任务的更高效的近似模型,给定前缀输入 x<t,从模型可以获得对应的分布 q(xt|x<t)。
论文"Speculative Decoding: Exploiting Speculative Execution for Accelerating Seq2seq Generation"确立了 草稿模型的两个原则:Capability Principle(尽可能准)和 Latency Principle(尽可能快)。另外需要注意的是,小模型的参数量要远小于原模型参数量一个级别才效果明显;草稿模型和原模型需要使用同样的tokenizer,不然会增加额外的解码、编码时间。
5.2.2 第一步 - 采样
对于输入prefix,在用LLM(目标模型)做推理的同时,并行地让草稿模型基于输入prefix以自回归的方式串行运行 \(\gamma\) 次,生成得到 \(\gamma\) 个token(称作guesses或draft tokens)。即,对于每个 \(i \in \gamma\),计算 \(q_i(x)\),其中 \(q_i\) 是 \(M_q\) 在 \(prefix+[x_1, ..., x_{i-1}]\) 上的分布,然后从这个分布\(q_i\)中采样一个token \(x_i\)。
5.2.3 第二步 - 并行运行目标模型
把生成的 \(\gamma\) 个tokens和前缀拼接一起送进目标模型\(M_p\)执行一次前向传播(验证模型把候选tokens输入采样以prefill的方式并行计算)。即,对于每个猜测的token \(x_i\),将它附加到前缀 \(prefix+[x_1, ..., x_{i-1}]\) 上,然后并行运行目标模型\(M_p\),分别得到了\(M_p\)的输出 \(p_1(x), ..., p_{γ+1}(x)\)。和自回归相比,尽管计算量一样,但是 \(\gamma\) 个tokens可以同时参与计算,计算访存比显著提升。
5.2.4 第三步 - 计算接受的猜测token数量
既然得到了目标模型和草稿模型的输出,我们就可以计算接受的猜测token数量。但是,如何评价一个token生成的好坏与否?这是通过比较 \(M_q\) 生成的猜测和 \(M_p\) 对这些猜测的评估概率(p,q表示在大小模型采样概率,也就是logits归一化后的概率分布)来决定的。即,依次使用每个 Token 对应的分布进行对比,找到满足要求的 Token 个数 n,或者说,根据p/q针对每个token进行拒绝采样,以此来确定接受的token数。
-
如果\(q(x) \leqslant p(x)\), 说明大模型在小模型采样出的这个token x上置信度更高,不需要再消减在这个token上的概率分布,就接受这个结果。
-
反之,如果q(x) > p(x),说明大模型在token x上的置信度低于小模型,那么需要把大模型在这个token上的一些采样概率分给其它大模型上信心更高的token,则以\(\frac{p(x)}{q(x)}\)的概率接受当前token,以\(1-\frac{p(x)}{q(x)}\)的概率丢弃x。
5.2.5 第四步 - 调整概率分布
这一步会依据需要来调整\(M_p\) 的分布。
- 如果接受的猜测token数量n小于γ,那么可能需要对 Mp 生成的分布进行调整,以确保接受的猜测与目标模型的输出分布保持一致。
- 具体是通过创建一个新的分布 \(p\prime (x) = norm(max(0,p_{n+1}(x) − q_{n+1}(x)))\)来调整。
需要注意的是,如果一个样本被拒绝,这意味着我们需要重新进行计算,这会导致一些计算资源的浪费。因此,在算法运行过程中,我们希望尽可能地接受 Mq 生成的样本,以减少计算成本。
我们后续会详细阐释调整概率分布的意义。
5.2.6 第五步 - 返回生成的结果
调整概率分布之后,会返回生成的结果。
-
如果小模型生成结果都满意,则用大模型采样下一个token。即,用 \(M_p\) 采样下一个token,加上 \(M_q\) 生成的 n 个 tokens,一并返回。
-
如果某一个token x 不满意,x 被拒绝,则从token x 之后的tokens都被丢弃。因为第四步已经调整了Mp的分布,会从这个新的概率分布\(p'(x) = norm(max(0, p(x) − q(x)))\)中重新采样一个token作为纠正。
因为加上了后面这个大模型拒绝采样,并补充大模型概率分布差采样的过程,所以上面这个采样过程和直接从p(x) 采样是等价的。
一共最多可以生成多少个token?如果把验证过程看成接受概率为\(\alpha\)的连续γ次判定过程,从上述算法流程知道输出token的长度范围是[1,γ+1],有以下3种情况
- 情况1:当第1个token就被大模型拒绝了,那么就直接用大模型的采样输出,生成长度为γ=1
- 情况2:当第t个token被大模型接受,但是第t+1个token被大模型拒绝的时候,生成长度为L=t+1。注意此时t≤γ−1
- 情况3:当所有k个token都被大模型接受,此时理应达到最大生成长度L=γ。但如果draft生成的γ个token都通过验证,那还可以从已经计算的第γ+1个token的logits中额外采样出一个,而且这个token是target模型生成的,也就不需要验证了。因此最终生成长度L=γ+1
5.3 重点分析
我们接下来看看投机解码中的一些重点。
5.3.1 并行验证
我们用示例来看看如何进行并行验证。
下图中,输入为:Our technique illustrated in the case of 。小模型串行生成三个token,小模型每次都是接受(1, vocal_size)的输入。具体参见下图标号1。
- 第1次推理,小模型生成 unconditional。
- 第2次推理,小模型生成 language。
- 第3次推理,小模型生成 modeling。
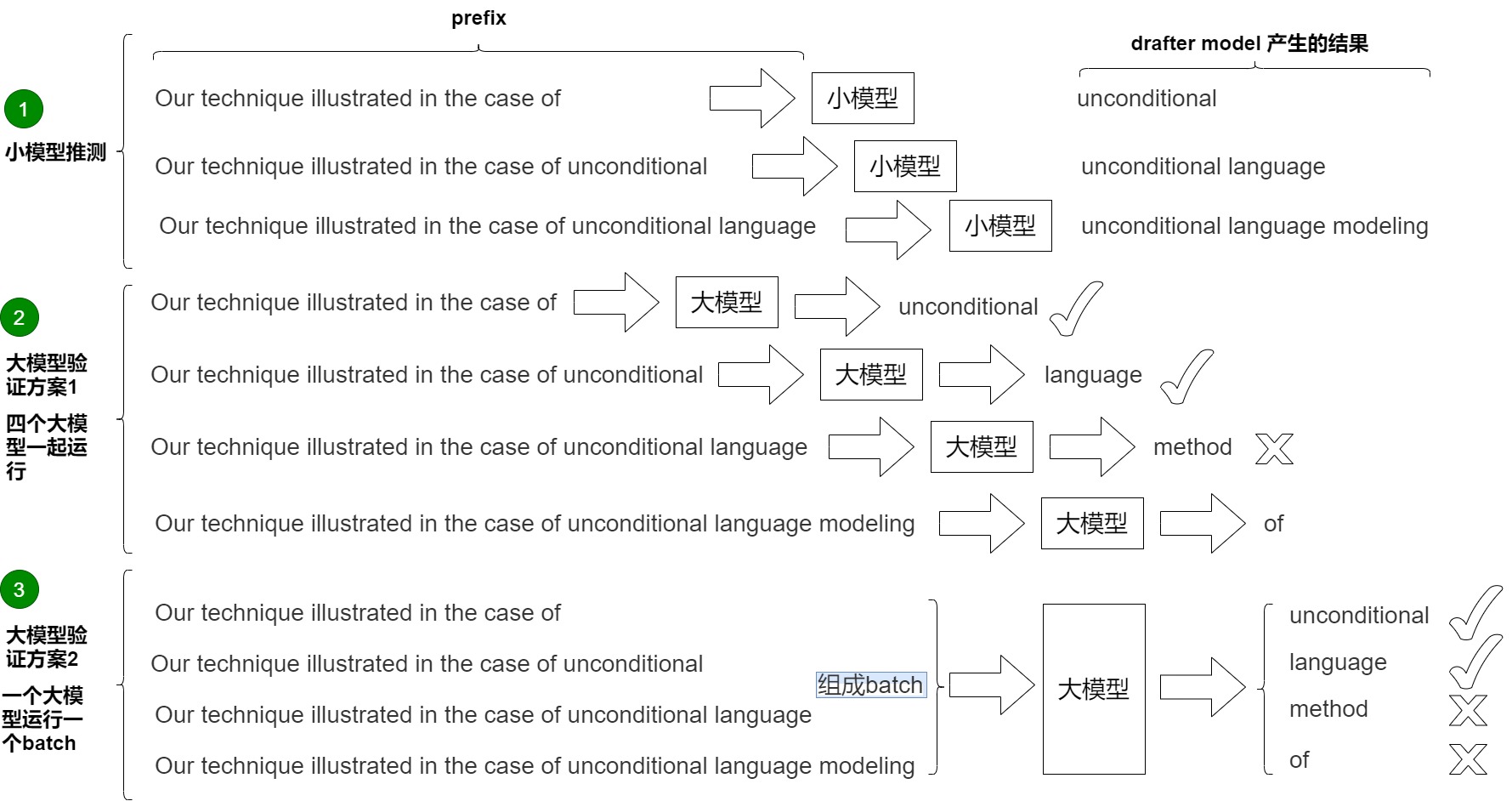
有两种方案来验证这些token。
方案1是论文中提出的方案,具体参见上图标号2。论文里的并行就是指一次计算多个token,节省传输损耗。然而,论文里对\(M_p\)进行并行计算,是一种不顾及计算资源的加速。它在每一步都尝试并行计算大模型的观点,从而达到速度上的最优化,但同时对并行计算能力要求极高。比如r为3时,就需要4个大模型同时计算。在极致并行的情况下,速度可以达到理论最优,但代价是算力的浪费,这在工程上是不可接受的。
方案2是实际工作中的方案,利用prefill阶段(并行处理多个token)比decoding阶段(串行生成多个token)计算效率高的特点来完成加速。target模型的任务不是生成,而是验证。由于现代计算机的并行能力,我们可以近似的认为大模型处理一个token和并行处理多个token的用时是几乎一样的。这就保证额验证这一过程可以并行实现,即调用一次target模型执行prefill操作,就可以完成对多个草稿模型(多个decoding步骤)的一次性验证,从而减少了推理步骤。同时,根据 Mq 对 Mp 的逼近程度,还可能生成多个新token,最多可以生成 γ + 1 个。上图标号3展示了这个过程。大模型一次性接受的是(3, vocal_size)的输入,即,直接检查unconditional "、"language "、"modeling" 这3个新token,所以叫并行。其思路和 LLM 训练阶段的交叉熵验证一样,通过错位方和矩阵计算的并行性,一步计算就可以验证小模型生成的3个结果对不对,即可完成验证。需要并行执行四次验证(以 argmax 为例):
- Prefix "Our technique illustrated in the case of",生成 "unconditional ",与近似模型生成的第一个 Token "unconditional " 相同,接受。
- Prefix "Our technique illustrated in the case of unconditional",生成 "language",与近似模型生成的第二个 Token "language" 相同,接受。
- Prefix "Our technique illustrated in the case of unconditional language",生成 "method",与近似模型生成的第三个 Token "modeling" 不相同,不接受。
- Prefix "Our technique illustrated in the case of unconditional language modeling",生成 "of",作为候选,如果前面都接受,则接受该 Token。
5.3.2 加速效果
实现加速的原理是什么?简而言之,投机解码相比自回归采样之所以有加速效果,是因为它减少了对原始模型串行调用的次数。因此,投机解码需要将以下两个步骤结合在一起,才能实现推理的加速。
- 草稿生成。Mq 生成 γ 个补全。因为draft模型参数量少,相比于target模型生成token更快,是更高效的模型 ,所以减少了生成补全的时间。
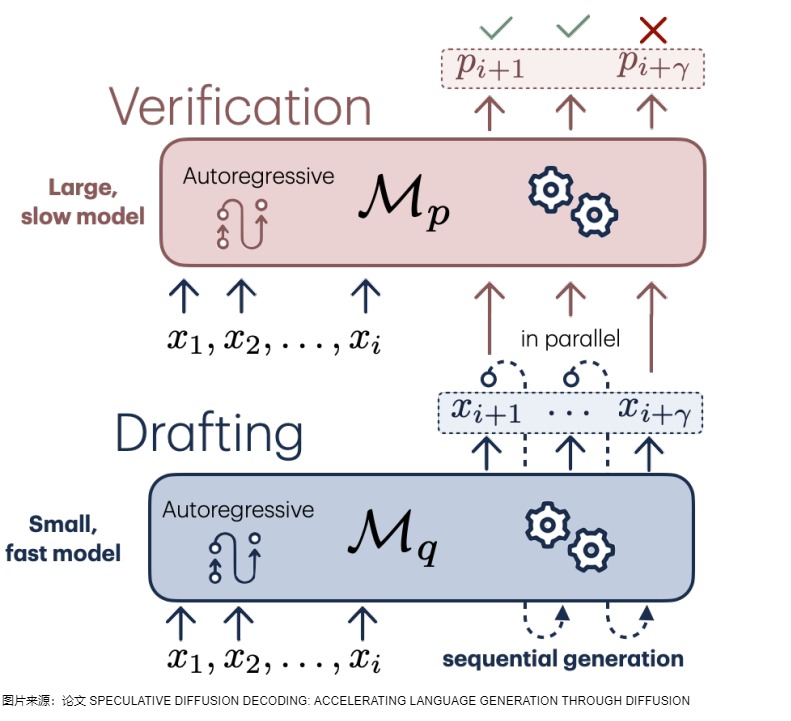
- 草稿校验。使用目标模型 Mp 并行评估来自 Mq 的所有猜测及其相应的概率,接受那些可以导致相同分布的猜测,并从调整后的分布中抽取额外的一个token,以修复第一个被拒绝的token,或者如果所有token都被接受,则添加一个额外的token。即,通过错位和矩阵计算的并行性,一步计算就可以验证小模型生成的 γ 个结果对不对。
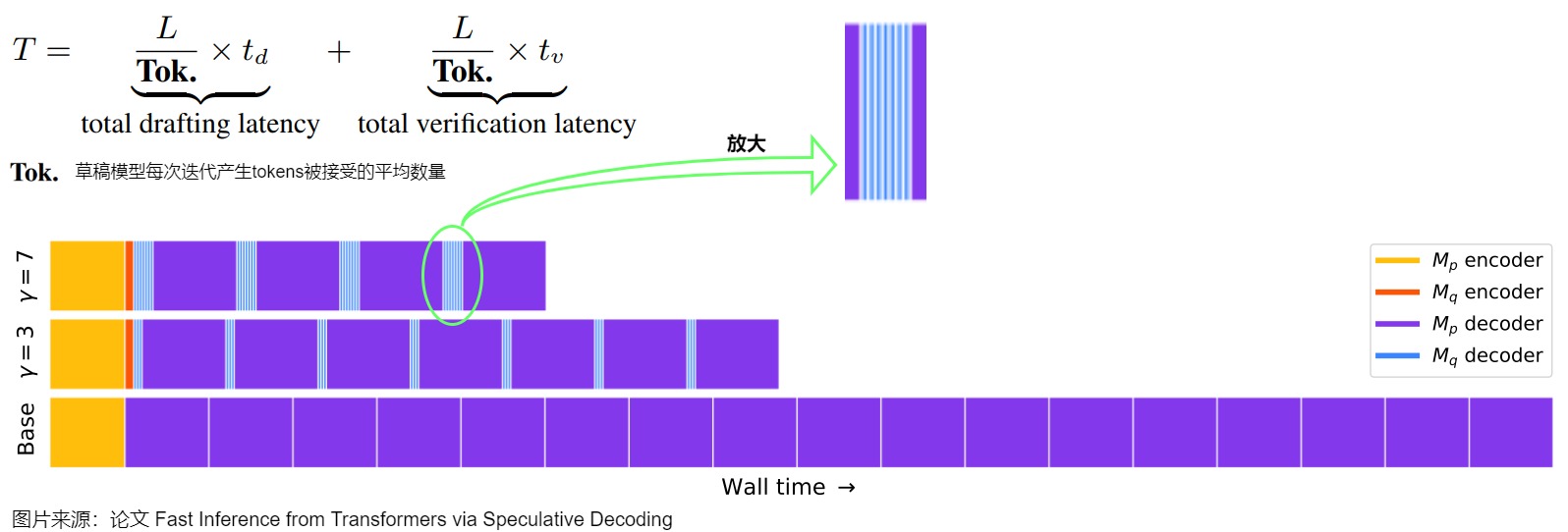
下图示例中包含不同的 𝛶(验证的 Token 数目),其中紫色为执行目标模型 Mp 的 decoder,蓝色为执行近似模型 Mq 的 decoder,黄色和橙色为调用 encoder。这里规定一次迭代可以接收小模型的tokens数为generated tokens。加速效果和 γ ,p,q都相关。直觉上讲,γ 越大,p、q分布越接近,则 generated tokens越大。
用通俗的话来解释。
- 最下方是大模型直接预测新的token,耗费时间太长。
- 中间和上方是先使用小模型预测 𝛶 个 token,然后大模型借助矩阵计算的并行特性,一次性就可以验证这 𝛶 个中,前面哪几个是对的。如果有对的,那就节约很多时间(因为小模型远小于大模型,所以小模型消耗的时间基本可以忽略不记)。
影响加速比的因素是:
- 小模型的尺寸及一次推理的token数目。
- 小模型生成候选tokens的时延。
- 大模型对小模型推理token的接受率,或者说小模型和大模型的Align程度。
因此,如果小模型的输出草稿接受率足够高,且生成候选tokens的时延不长,那么投机解码就能够获得更高的加速比。假设我们一次猜n个tokens,平均有m个token会被最终接收,那么在这个过程中:我们调用了n次小模型D,1次大模型T,生成了m个token。只要nD显著地小于(m-1)T,就能实现很好的加速效果。
理解了原理,我们就可以知道这个方法加速的限制:小模型生成的分布是否与大模型一致。验证的接受率会很大程度上影响最终的加速比,接受率越高,减少的 Decoding Step 数量就越多,因未接收而浪费的计算就越少。
5.3.3 调整分布
我们提出一个问题:在算法的第四步,当 n < γ 时,为什么需要调整从目标模型(Mp)得到的分布?这个调整的目的是什么?
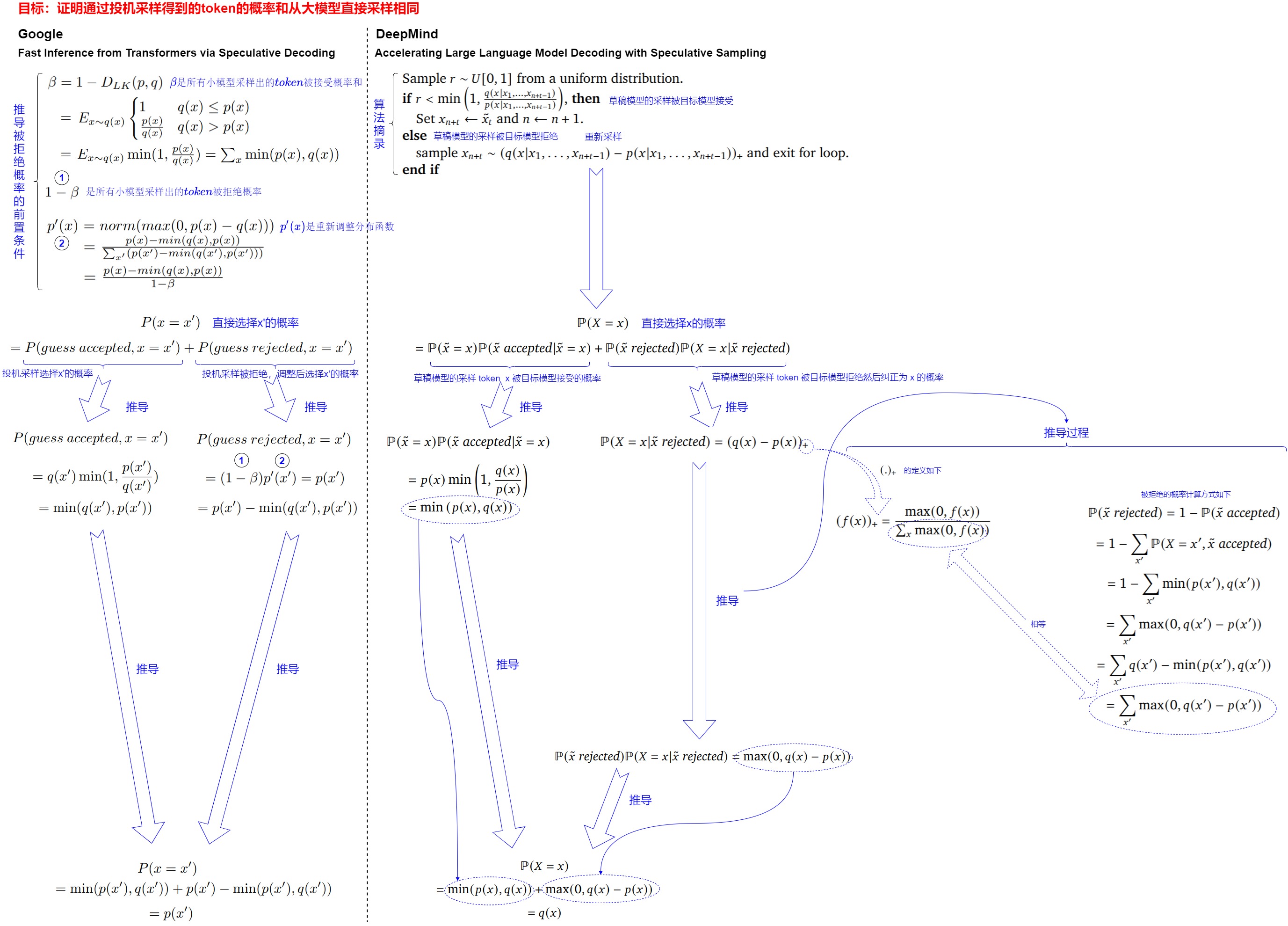
这就涉及到投机解码的另外一个核心:如何确保通过投机解码得到的token的概率和从大模型直接采样相同。事实上,投机解码和投机解码两篇论文都给出了证明:这种验证和重采样过程在理论等价于直接从目标 LLM 采样,因此,可以保证最终生成的文本分布与目标 LLM 一致。即,对于任意分布p(x)和q(x),通过从p(x)和q(x)进行投机解码所得到的token的分布与仅从p(x)进行采样所得到的token的分布是相同的。
我们首先概述下如何证明。本质上我们想考察的是\(p(x=\tilde x)\)的概率,在使用了投机解码策略之后,是否还依然等于我们的原始概率\(q(x=\tilde x)\),即\(q(\tilde x)\)。概率拆解思路为:有两种可能采样出\(\tilde x\),可以证明通过重采样之后,总体概率和原始概率一致。
- 路径1:小模型p(⋅|⋅)采样出了\(\tilde x\),并且成功的接受了。注意,如果此时对\(\tilde x\)发生了拒绝,是不可能通过重采样得到\(\tilde x\)。原因是,发生拒绝就说明\(q(\tilde x)\)小于\(p(\tilde x)\),因此在重采样中\(max(q(\tilde x)−p(\tilde x),0)\)为0,不可能重采样出\(\tilde x\)。
- 路径2:小模型p(⋅|⋅)采样得到了其他值\(x≠\tilde x\),并且发生了拒绝,此时重采样得到\(\tilde x\)。
其次,详细推导流程参见下图,我们基于论文 "Accelerating Large Language Model Decoding with Speculative Sampling" 的公式进行整理和注释。
产生偏差
当 n < γ 时,意味着从更高效的近似模型 Mq 中采样的token数量少于 γ,也就是说,其中一些猜测被目标模型 Mp 拒绝了。这可能是因为 \(M_q\) 生成的猜测与目标模型 \(M_p\) 的真实分布存在一定的偏差。
当使用这个近似模型 \(M_q\) 生成的token的概率小于或等于目标模型 \(M_p\) 生成这个 token 的概率时,我们会保留这个token。当近似模型 \(M_q\) 生成的token的概率大于目标模型 \(M_p\) 生成这个 token 的概率时,我们不能简单地接受这个token,因为这可能会导致生成的结果与目标模型的分布不一致。因此,在这种情况下,我们会以一定的概率拒绝这个token,并重新从调整后的概率分布中重新采样。
注:快速理解,如果 \(M_p\) 生成某个token的概率是0.5,\(M_q\) 生成该token的概率是0.6,说明 \(M_q\)已经比大模型还飘,不可信了。
弥补偏差
调整目标模型 \(M_p\) 分布的目的是为了弥补从近似模型 \(M_q\) 中得到的猜测与目标模型 \(M_p\) 分布之间的差异,以保证最终生成的结果符合目标模型的真实分布。这样可以确保在猜测性解码过程中得到的结果保持了一定的准确性和一致性。
调整分布操作弥补了小模型 \(M_q\) 和大模型 \(M_p\) 之间的概率分布的gap。思路是:对于小模型 \(M_q\) 的每一次猜测,根据大模型 \(M_p\) 和小模型 \(M_q\) 的概率分布去判断这一次猜测有多大概率是正确的。相当于是从小模型 \(M_q\) 的采样到大模型 \(M_p\) 的采样之间做了一个映射。可以把小模型 \(M_q\) 和大模型 \(M_p\) 的概率分别看成若干个随机事件,然后将小模型 \(M_q\) 的随机事件和大模型 \(M_p\) 的随机事件做映射,如果两边的随机事件的结果一致,我们就认为这个猜测是正确的。特别地,如果两个概率分布一样,则猜测正确的概率为1。如果在某一步中,我们认为小模型 \(M_q\) 的猜测是错误的,那么后面的结果都是无效的。此时用大模型 \(M_p\) 最后一步得到的概率分布做一个采样后退出。这一步既是保证输出是同分布的,又可以保证每次至少输出一个token。
具体来说,作者需要定义一个新的分布 \(p'(x)\),它是根据目标模型 \(M_p\) 的原始输出分布 \(p_{n+1}(x)\) 调整而来的。如果 n < γ(即目标模型拒绝了一些猜测),作者使用了一个调整函数来修改 \(p_{n+1}(x)\)。这个调整函数是 \(max(0, p_{n+1}(x) - q_{n+1}(x))\),它的作用是确保 \(p_{n+1}(x)\) 不小于 \(q_{n+1}(x)\)。这样做的目的是为了尽量保持目标模型生成的分布与近似模型的分布一致。
这里给一个直观的解释。这个调整后的概率分布\(p'(x)\)是通过将目标模型的概率分布(p(x))与来自近似模型的概率分布(q(x))进行相减,并取结果的最大值,然后将其归一化得到的。这个调整后的分布确保了我们从目标模型中采样的结果具有相同的分布特性,同时也能够处理那些被拒绝的token,保证最终的生成结果保持一致性。
p(x') > q(x')说明大模型在token x'上概率大于小模型,则大模型对生成token x'更有把握,说明小模型生成的问题不大,可以保留x'。如果p(x') ≤ q(x')则小模型更有把握,大模型就以1-p(x)/q(x)为概率概率拒绝,并重新采样。因为接收的概率更偏向q(x)大的位置,重新采样的概率应该更偏向p(x)大的位置,所以是norm(max(0, p(x)-q(x))。
弥补结果
从调整后的分布中生成一个额外的 Token(根据第一个出错 Token 之前的 Token 生成),来修复第一个出错的 Token,如果所有 Token 都被接受,则额外新增一个新生成的 Token(这个token是target模型生成的,也就不需要验证了),以此来保证每次至少生成一个新的 Token。这样,即使在最坏情况下,目标模型相当于完全串行运行,运行次数也不会超过常规模式直接串行运行目标模型的次数(每个目标模型的并行运行至少会生成一个新的标记);当然,也很可能能够生成更多的 Token,最多可以达到 𝛶+1,这取决于近似模型 Mq 对目标模型 Mp 的逼近程度。
5.3.4 优化
在推测解码方法中,草稿token的接受率受到草稿模型的输出分布与原始大模型的输出分布的一致程度的显著影响。因此,大量的研究工作都是在改进草稿模型。
DistillSpec直接从目标大模型中提取较小的草稿模型。SSD包括从目标大模型中自动识别子模型(模型层的子集)作为草稿模型,从而消除了对草稿模型进行单独训练的需要。OSD动态调整草稿模型的输出分布,以匹配在线大模型服务中的用户查询分布。它通过监视来自大模型的被拒绝的草稿token,并使用该数据通过蒸馏来改进草稿模型来实现这一点。PaSS提出利用目标大模型本身作为草稿模型,将可训练的token(lookahead token)作为输入序列,以同时生成后续token。REST引入了一种基于检索的推测解码方法,采用非参数检索数据存储作为草稿模型。SpecInfer引入了一种集体提升调优技术来对齐一组草稿模型的输出分布通过目标大模型。Lookahead decoding 包含大模型并行生成n-grams来生成草稿token。Medusa对大模型的几个头进行微调,专门用于生成后续的草稿token。Eagle采用一种称为自回归头的轻量级Transformer层,以自回归的方式生成草稿token,将目标大模型的丰富上下文特征集成到草稿模型的输入中。
另一项研究侧重于设计更有效的草稿构建策略。传统的方法通常产生单一的草稿token序列,这对通过验证提出了挑战。对此,Spectr主张生成多个草稿token序列,并采用k-sequential草稿选择技术并发验证k个序列。该方法利用推测抽样,确保输出分布的一致性。类似地,SpecInfer采用了类似的方法。然而,与Spectr不同的是,SpecInfer将草稿token序列合并到一个"token tree"中,并引入了一个用于验证的树形注意力机制。这种策略被称为"token tree verifier"。由于其有效性,token tree verifier在众多推测解码算法中被广泛采用。除了这些努力之外,Stage Speculative Decoding和Cascade Speculative Drafting(CS Drafting)建议通过将投机解码直接集成到token生成过程中来加速草稿构建。
0x06 实现
我们使用 https://github.com/huggingface/transformers/src/transformers/generation/utils.py来进行学习。
6.1 全局循环
在_assisted_decoding()函数中的while循环里面进行投机解码。
python
def _assisted_decoding(
self,
input_ids: torch.LongTensor,
candidate_generator: CandidateGenerator,
logits_processor: LogitsProcessorList,
stopping_criteria: StoppingCriteriaList,
generation_config: GenerationConfig,
synced_gpus: bool,
streamer: Optional["BaseStreamer"],
**model_kwargs,
) -> Union[GenerateNonBeamOutput, torch.LongTensor]:
# init values
do_sample = generation_config.do_sample
output_attentions = generation_config.output_attentions
output_hidden_states = generation_config.output_hidden_states
output_scores = generation_config.output_scores
output_logits = generation_config.output_logits
return_dict_in_generate = generation_config.return_dict_in_generate
# init attention / hidden states / scores tuples
scores = () if (return_dict_in_generate and output_scores) else None
raw_logits = () if (return_dict_in_generate and output_logits) else None
decoder_attentions = () if (return_dict_in_generate and output_attentions) else None
cross_attentions = () if (return_dict_in_generate and output_attentions) else None
decoder_hidden_states = () if (return_dict_in_generate and output_hidden_states) else None
# if model is an encoder-decoder, retrieve encoder attention weights and hidden states
if return_dict_in_generate and self.config.is_encoder_decoder:
encoder_attentions = model_kwargs["encoder_outputs"].get("attentions") if output_attentions else None
encoder_hidden_states = (
model_kwargs["encoder_outputs"].get("hidden_states") if output_hidden_states else None
)
# keep track of which sequences are already finished
batch_size = input_ids.shape[0]
unfinished_sequences = torch.ones(batch_size, dtype=torch.long, device=input_ids.device)
model_kwargs = self._get_initial_cache_position(input_ids, model_kwargs)
this_peer_finished = False
is_first_iteration = True # to preserve the same API in the output as other generation methods
# while循环里面进行投机解码
while self._has_unfinished_sequences(this_peer_finished, synced_gpus, device=input_ids.device):6.2 外层逻辑
此处包括获取草稿模型的输出,调用论文的算法,依据算法结果对token进行调整。
python
while self._has_unfinished_sequences(this_peer_finished, synced_gpus, device=input_ids.device):
cur_len = input_ids.shape[-1]
# 1. Fetch candidate sequences from a `CandidateGenerator` and move to the correct device
candidate_input_ids, candidate_logits = candidate_generator.get_candidates(input_ids)
candidate_input_ids = candidate_input_ids.to(self.device)
if candidate_logits is not None:
candidate_logits = candidate_logits.to(self.device)
candidate_length = candidate_input_ids.shape[1] - input_ids.shape[1]
is_done_candidate = stopping_criteria(candidate_input_ids, None)
# 2. Use the original model to obtain the next token logits given the candidate sequence. We obtain
# `candidate_length + 1` relevant logits from this process: in the event that all candidates are correct,
# we use this forward pass to also pick the subsequent logits in the original model.
# 2.1. Prepare the model inputs
candidate_kwargs = copy.copy(model_kwargs)
candidate_kwargs = _prepare_attention_mask(
candidate_kwargs, candidate_input_ids.shape[1], self.config.is_encoder_decoder
)
candidate_kwargs = _prepare_token_type_ids(candidate_kwargs, candidate_input_ids.shape[1])
if "cache_position" in candidate_kwargs:
candidate_kwargs["cache_position"] = torch.cat(
(
candidate_kwargs["cache_position"],
torch.arange(cur_len, cur_len + candidate_length, device=input_ids.device, dtype=torch.long),
),
dim=0,
)
model_inputs = self.prepare_inputs_for_generation(candidate_input_ids, **candidate_kwargs)
if "logits_to_keep" in model_inputs:
model_inputs["logits_to_keep"] = candidate_length + 1
# 2.2. Run a forward pass on the candidate sequence
# prepare variable output controls (note: some models won't accept all output controls)
model_inputs.update({"output_attentions": output_attentions} if output_attentions else {})
model_inputs.update({"output_hidden_states": output_hidden_states} if output_hidden_states else {})
outputs = self(**model_inputs)
# 2.3. Process the new logits
# .float() is needed to retain precision for later logits manipulations
new_logits = outputs.logits[:, -candidate_length - 1 :].float() # excludes the input prompt if present
new_logits = new_logits.to(input_ids.device)
next_token_logits = new_logits.clone()
if len(logits_processor) > 0:
for i in range(candidate_length + 1):
new_logits[:, i, :] = logits_processor(candidate_input_ids[:, : cur_len + i], new_logits[:, i, :])
# 3. Select the accepted tokens. There are two possible cases:
# Case 1: `do_sample=True` and we have logits for the candidates (originally from speculative decoding)
# 👉 Apply algorithm 1 from the speculative decoding paper (https://arxiv.org/pdf/2211.17192.pdf).
if do_sample and candidate_logits is not None:
valid_tokens, n_matches = _speculative_sampling(
candidate_input_ids,
candidate_logits,
candidate_length,
new_logits,
is_done_candidate,
)
# Case 2: all other cases (originally from assisted generation) 👉 Compare the tokens selected from the
# original model logits with the candidate tokens. We can keep the candidate tokens until the first
# mismatch, or until the max length is reached.
else:
if do_sample:
probs = new_logits.softmax(dim=-1)
selected_tokens = torch.multinomial(probs[0, :, :], num_samples=1).squeeze(1)[None, :]
else:
selected_tokens = new_logits.argmax(dim=-1)
candidate_new_tokens = candidate_input_ids[:, cur_len:]
n_matches = ((~(candidate_new_tokens == selected_tokens[:, :-1])).cumsum(dim=-1) < 1).sum()
# Ensure we don't generate beyond max_len or an EOS token
if is_done_candidate and n_matches == candidate_length:
n_matches -= 1
valid_tokens = selected_tokens[:, : n_matches + 1]
# 4. Update variables according to the number of matching assistant tokens. Remember: the token generated
# by the model after the last candidate match is also valid, as it is generated from a correct sequence.
# Because of this last token, assisted generation search reduces to a normal greedy search/sample if there
# is no match.
# 4.1. Get the valid continuation, after the matching tokens
input_ids = torch.cat((input_ids, valid_tokens), dim=-1)
if streamer is not None:
streamer.put(valid_tokens.cpu())
new_cur_len = input_ids.shape[-1]
# 4.2. Discard past key values relative to unused assistant tokens
new_cache_size = new_cur_len - 1
outputs.past_key_values = _crop_past_key_values(self, outputs.past_key_values, new_cache_size)
# 5. Update the candidate generation strategy if needed
candidate_generator.update_candidate_strategy(input_ids, new_logits, n_matches)6.3 实施算法
注释中写到,实现了论文"Fast Inference from Transformers via Speculative Decoding"的算法1,即如下算法。

代码如下。
python
def _speculative_sampling(
candidate_input_ids,
candidate_logits,
candidate_length,
new_logits,
is_done_candidate,
):
"""
Applies sampling as in the speculative decoding paper (https://arxiv.org/pdf/2211.17192.pdf, algorithm 1). Returns
the selected tokens, as well as the number of candidate matches.
NOTE: Unless otherwise stated, the variable names match those in the paper.
"""
new_candidate_input_ids = candidate_input_ids[:, -candidate_length:]
# Gets the probabilities from the logits. q_i and p_i denote the assistant and model probabilities of the tokens
# selected by the assistant, respectively.
q = candidate_logits.softmax(dim=-1)
q_i = q[:, torch.arange(candidate_length), new_candidate_input_ids].squeeze(0, 1)
p = new_logits.softmax(dim=-1)
p_i = p[:, torch.arange(candidate_length), new_candidate_input_ids].squeeze(0, 1)
probability_ratio = p_i / q_i
# When probability_ratio > 1 (i.e. q_i(x) < p_i(x), or "assistant probability of the candidate token is smaller
# than the model probability for the same token"), keep the token. Otherwise reject with p = 1 - probability_ratio
# (= keep with p = probability_ratio). Keep all the tokens until the first rejection
r_i = torch.rand_like(probability_ratio)
is_accepted = r_i <= probability_ratio
n_matches = ((~is_accepted).cumsum(dim=-1) < 1).sum() # this is `n` in algorithm 1
# Ensure we don't generate beyond max_len or an EOS token (not in algorithm 1, but needed for correct behavior)
if is_done_candidate and n_matches == candidate_length:
# Output length is assumed to be `n_matches + 1`. Since we won't generate another token with the target model
# due to acceptance on EOS we fix `n_matches`
n_matches -= 1
valid_tokens = new_candidate_input_ids[:, : n_matches + 1]
else:
# Next token selection: if there is a rejection, adjust the distribution from the main model before sampling.
gamma = candidate_logits.shape[1]
p_n_plus_1 = p[:, n_matches, :]
if n_matches < gamma:
q_n_plus_1 = q[:, n_matches, :]
p_prime = torch.clamp((p_n_plus_1 - q_n_plus_1), min=0)
p_prime.div_(p_prime.sum())
else:
p_prime = p_n_plus_1
t = torch.multinomial(p_prime, num_samples=1).squeeze(1)[None, :]
# The selected tokens include the matches (if any) plus the next sampled tokens
if n_matches > 0:
valid_tokens = torch.cat((new_candidate_input_ids[:, :n_matches], t), dim=-1)
else:
valid_tokens = t
return valid_tokens, n_matches0x07 Token Tree Verification
因为Token Tree Verification的重要性,我们单独用一节来进行阐释。
前文提到过,Token Tree Verification使目标LLM能够并行验证多个草稿序列。其思路就是:让草稿模型在每个时间步都输出k个候选token,然后通过共享前缀从多个候选token序列建立一个trie,并从trie树中修剪不太频繁的节点。最后在一次运行中用树注意力对其进行并行验证(子token被注意力掩蔽,只能看到其父token)。
7.1 问题
7.1.1 采样多个序列
论文"SpecInfer: Accelerating Generative Large Language Model Serving with Tree-based Speculative Inference and Verification"发现,大模型验证失败的时候,真实生成的token大多数时候其实也是小参数模型的top-k的tokens。下图展示了使用greedy和stochastic decoding两种方法topK里面k从1到5在各个数据集上的验证成功率。可以看出,尽管预测next next token的top-1准确率徘徊在60%左右,但是在小参数模型每一个step都保留top-5的时候,最后的验证成功率都大大提高。如果使用necleus sampling,top-3的成功率就已经超过了90%。
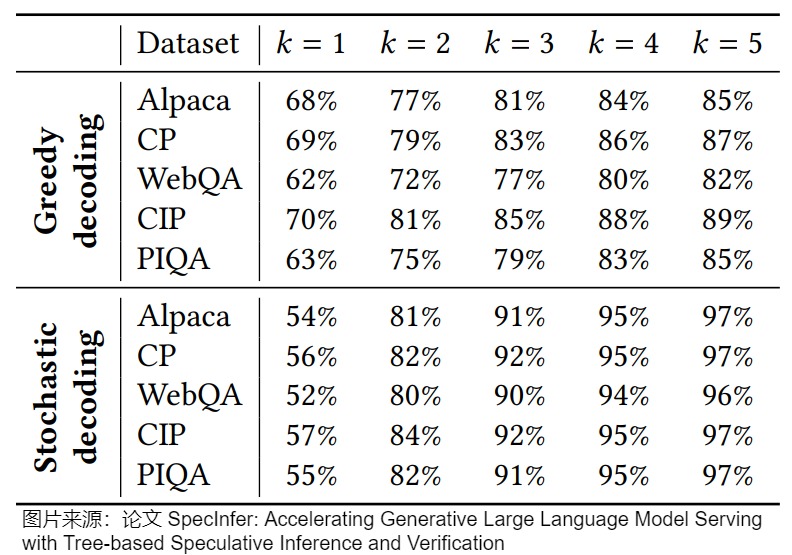
基于此,我们不应该采样一个单独的序列型的的tokens,而是采样一个树状的token树。不止在第一步猜k个token,我们可以在每一步都猜多个tokens,这样每一步的几率都会变大。只要由此带来的额外的计算开销小于更高的带来的加速,那么猜更多的token就是可以接受的。
7.1.2 验证多个序列
但是,如何对这个token树进行验证?即,如何组织多个序列的输入?组织多个序列的输入最简单的方法就是直接把每一个叶子节点到根节点的所有token组成一个序列,然后进行验证,这种方案存在几个问题:
- 逐一连续验证这些token会有冗余计算的问题,将过于耗时。
- 一些工作发现,一次预测一条链的话,概率衰减的非常快,所以不能预测很长的链,导致不能充分利用上大模型验证的并行度。
另一个方法是把每一个叶子节点到根节点的所有token组成一个序列,n多个叶子节点就会组成n个序列,然后把这n个序列当成batch size=n的输入进行prefill。然而这种方式的问题是根节点的计算不能被复用。
我么接下来看看研究人员是如何解决上述问题。
7.2 思路
7.2.1 开山之作SpecInfer
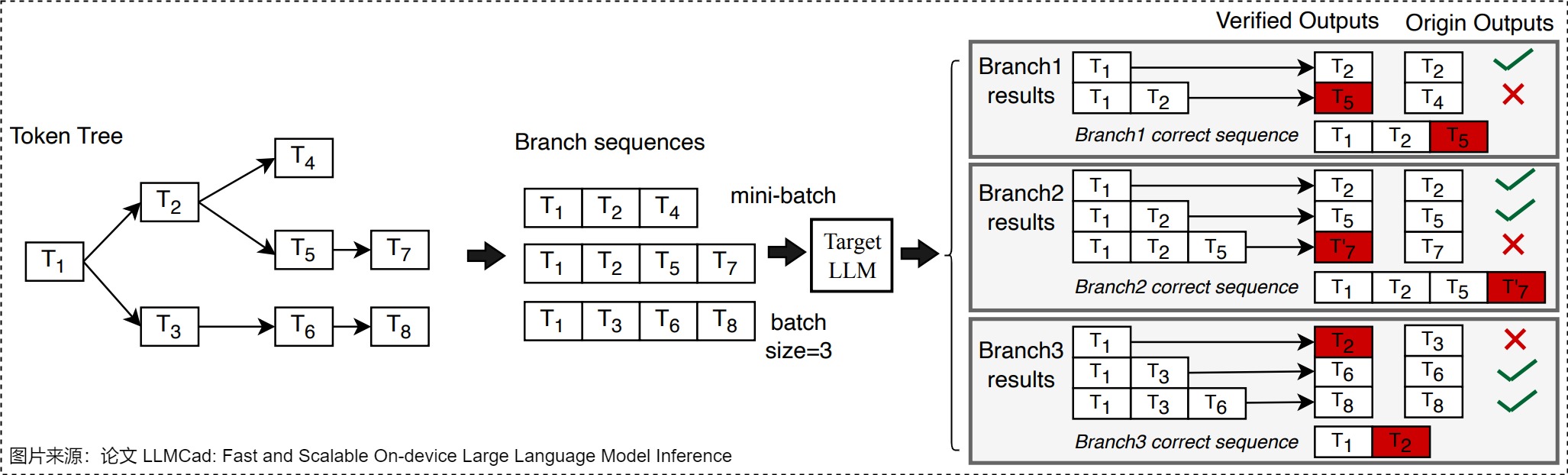
为了解决上述问题,SpecInfer设计了 Tree Based Parallel Decoding 机制。其核心思路为:通过一系列小模型 SSM(Small Speculative Model)联合预测 LLM 输出,并将这些小模型的预测输出组织为 Token 树,树中每个分支表示一个唯一的候选 Token 序列。最后,LLM 使用基于树的并行解码(Tree-Based Parallel Decoding)机制来并行的验证 Token 树中所有 Token 的正确性,这里树的解码算法还可以重用这些序列之间共享的中间结果。SpecInfer 使用 LLM 作为 Token 树验证器而非增量解码器,这显著降低了生成式 LLM 的端到端延迟,同时可以保持模型的质量。
SpecInfer的具体流程如下。
-
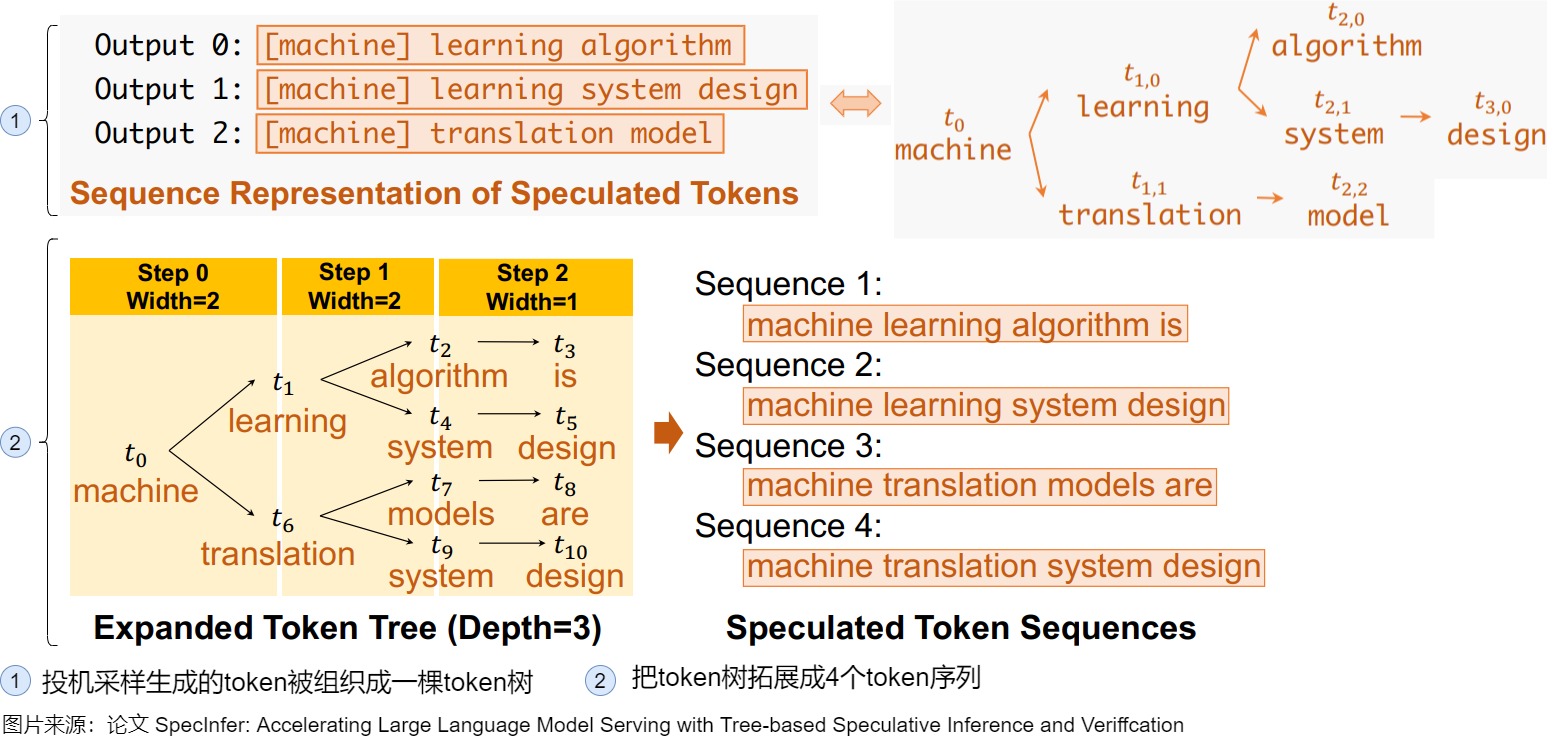
先为每个 SSM 生成了一棵输出树,即在每个 token 取若干种可能性构成一棵树,之后将这些树合并成一棵更大的树。当生成更大的树之后,把该树拓展成若干个token序列。
-
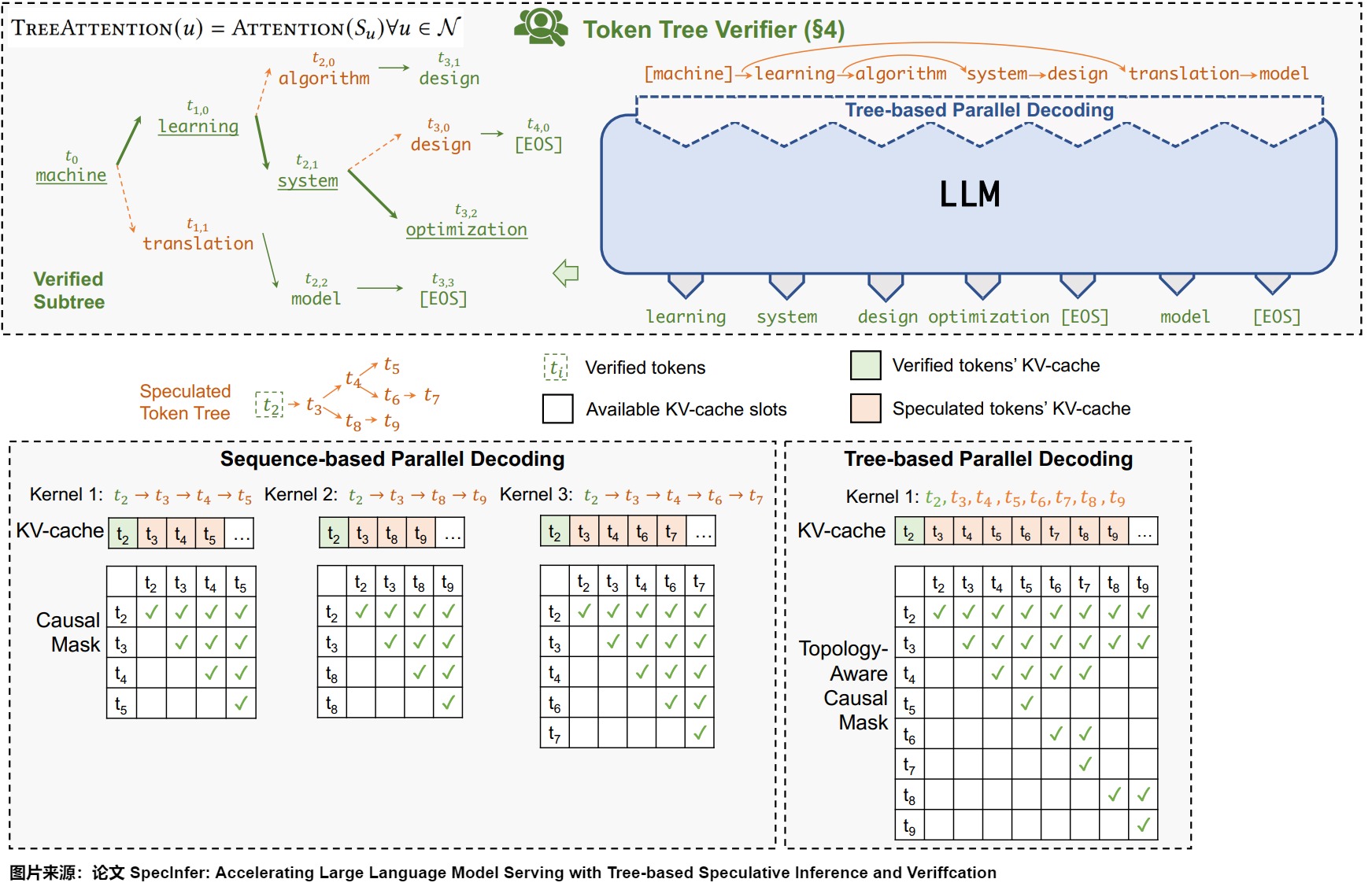
将生成的树进行验证。树结构会带来token之间复杂的依赖关系,如果对树上的每一个从root到leaf的路径都用大模型做一次验证,大量的叶子节点也会导致算法退化到最原始的一次预测一个token的场景。针对这个情况,SpecInfer提出了tree attention来加速decoding的速度。方法是将树上的祖先关系变成attention-mask的可见关系,使得模型可以一次验证多个 sequence。如下图所示,对于这样一棵树,如果采用常规的 mask 方式,t6 是可以看到 t5 的,但在图上的 mask 矩阵下,每个 token 只可以看到自己的 prefix,从而使得 LLM 可以一次完成对于多个 sequence 的不互相干扰的验证。
7.2.2 如何组织树
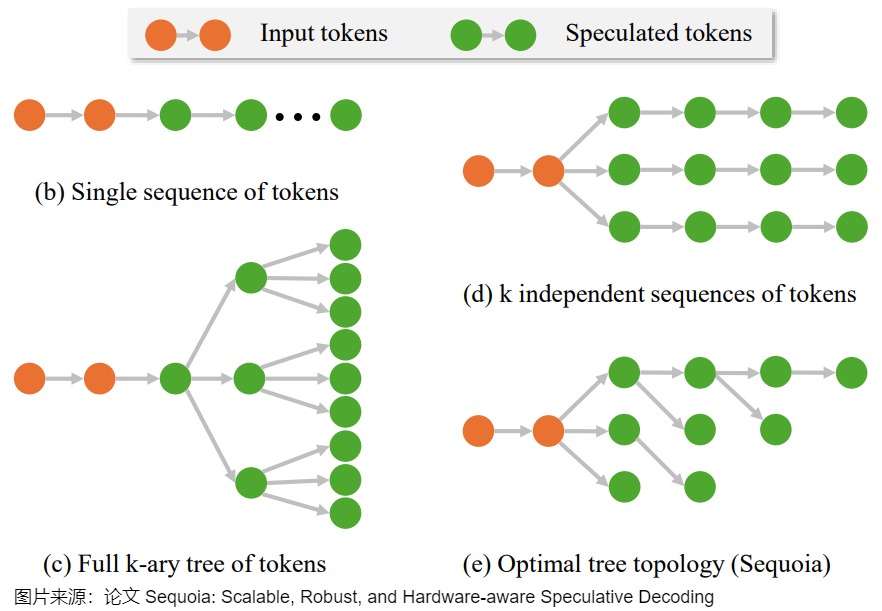
有多种组织树的方法,具体参见下图。
以下图右下角的Sequoia为例,接受向量是p=(p1,p2,...,pk,...),其中验证算法在子位置k接受token的概率为pk。树的具体构建方法基于 positional acceptance assumption:假设token t 是已接受token的第k个子token,则验证算法接受token t 的概率仅取决于 k 的值 。每个子节点的得分为从根节点到此节点的所有 \(p_k\) (验证算法在子位置 k 接受token的概率)相乘。最后的目标是,在给定节点数量的情况下使整棵树所有节点得分相加最大。这个问题的解可以用更小的子问题的解来表示,因此可以通过动态规划求解。求得的树结构满足预测概率较大的子节点会有更多的子孙。
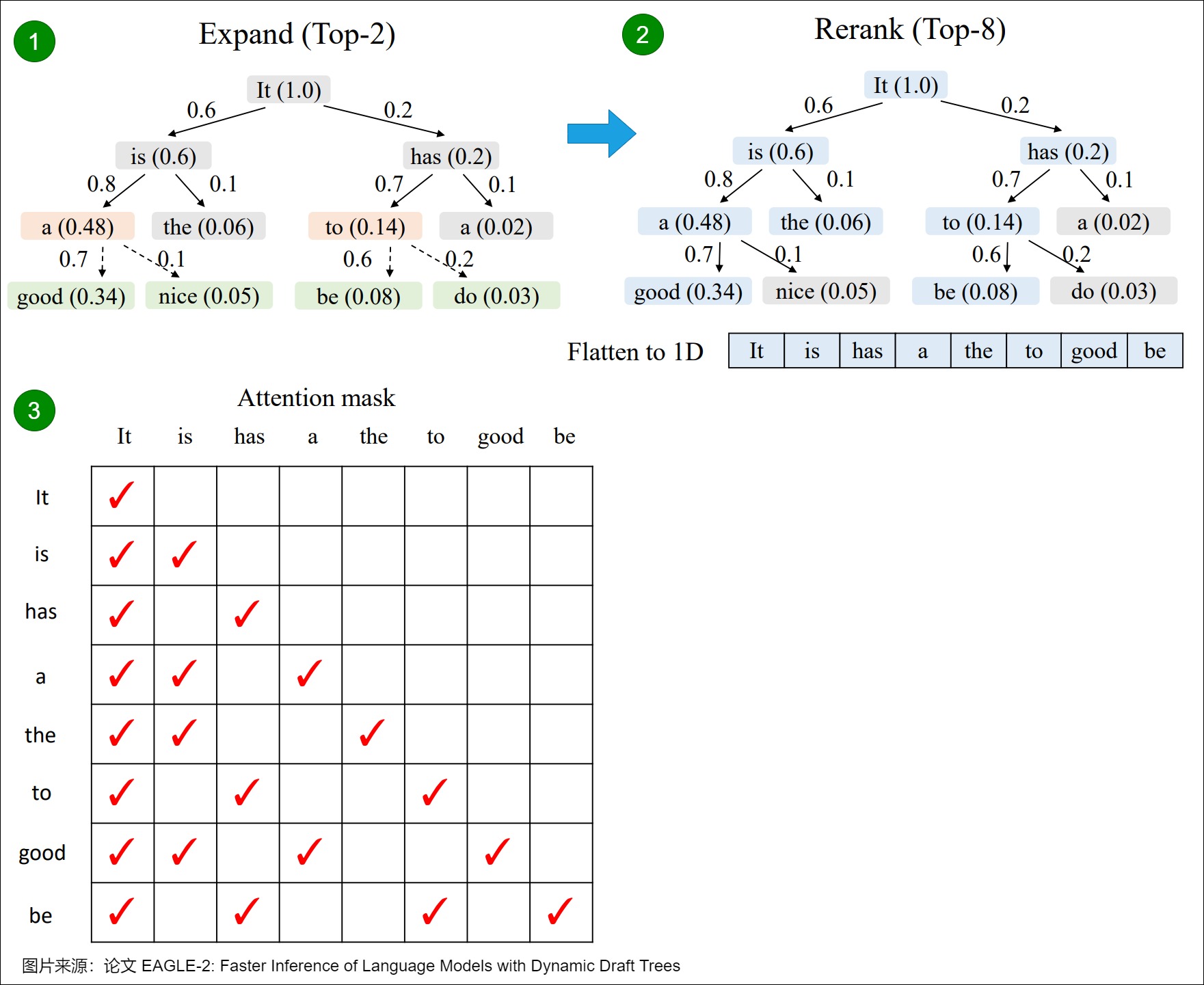
再比如,下图给出了EAGLE-2的Token Tree Verification。树的边上的数字表示草稿模型的置信度得分,块内括号中的数字表示节点的值。在扩展阶段,我们从当前层(橙色块)中选择值最高的前2个节点作为草稿模型的输入,并将生成的token(绿色块)连接到草稿树。在重新排序阶段,我们从所有节点(蓝色块)中选择值最高的前8个节点,将其展平为一维序列以形成最终草稿。然后,我们根据树结构来构建注意力掩码,确保每个token只能看到其祖先节点。
7.3 Attention Mask
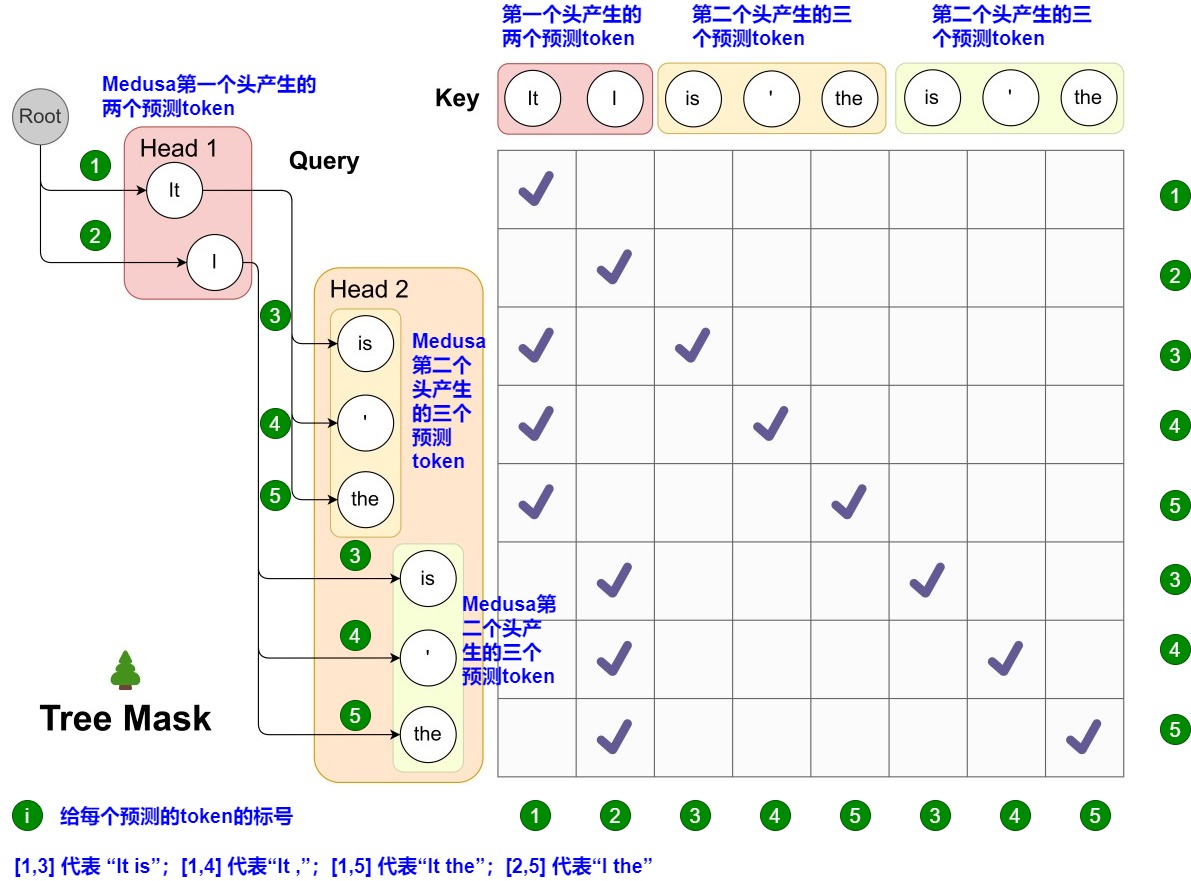
Medusa 中的 Attention Mask 矩阵如下图所示。左侧给出了候选序列。而其对应的 Attention Mask 矩阵如右侧所示。在图上,Head 1 在下一个位置生成 2 个可能的 Token(It 和 I),Head 2 在下下一个位置生成 3 个可能的 Token(is,' 和 the)。因为第一个头部的任何预测都可以与第二个头部的任何预测配对,这样下一个位置和下下一个位置就有了 2 x 3 = 6 种可能的候选序列,最终形成一个多层树结构。这棵树的每一层都对应于一个Medusa Head的预测。在这棵树内,Attention Mask只限制一个token对其前面token的注意力。
0xFF 参考
加速大模型之投机采样(Speculative Decoding) 杜凌霄
Speculative Decoding: Exploiting Speculative Execution for Accelerating Seq2seq Generation]
[paper reading](https://zhuanlan.zhihu.com/p/684204483)
LLM推理加速新范式!推测解码(Speculative Decoding)最新综述 hemingkx
有没有speculative decoding的综述? 木叶
3万字详细解析清华大学最新综述工作:大模型高效推理综述 zenRRan
LLM推理加速: Speculative Decoding 概述 zssloth
加速大模型之投机采样(Speculative Decoding) 杜凌霄
deepseek技术解读(2)-MTP(Multi-Token Prediction)的前世今生 姜富春
[读书笔记]Multi-token prediction 多词预测 迷途小书僮
Deepseek-v3技术报告-图的逐步解析-3-不容易看懂的MTP-公式有拼写错误 迷途小书僮
万字综述 10+ 种 LLM 投机采样推理加速方案 AI闲谈
https://github.com/hemingkx/SpeculativeDecodingPapers
【手撕LLM-Speculative Decoding】大模型迈向"并行"解码时代 小冬瓜AIGC
【手撕LLM-Medusa】并行解码范式: 美杜莎驾到, 通通闪开!! 小冬瓜AIGC
https://zhuanlan.zhihu.com/p/684217993
https://mp.weixin.qq.com/s/PyAKiFzbQNq6w7HmaTnSEw
https://zhuanlan.zhihu.com/p/690504053
https://zhuanlan.zhihu.com/p/699166575
https://zhuanlan.zhihu.com/p/658298728
LLM推理加速之Medusa:Blockwise Parallel Decoding的继承与发展 方佳瑞
方佳瑞:LLM推理加速的文艺复兴:Noam Shazeer和Blockwise Parallel Decoding 方佳瑞
Accelerating Large Language Model Decoding with Speculative Sampling Charlie Chen, Sebastian Borgeaud, Geoffrey Irving, Jean-Baptiste Lespiau, Laurent Sifre and John Jumper All authors from DeepMind
Speculative Decoding 论文阅读合订本 灰瞳六分仪
推测解码算法(Speculative Decoding)快速理解与代码实现 iyayaai
猜测解码(speculative decoding)的等效性证明 paperplanet
大模型推理妙招---投机采样(Speculative Decoding) 方佳瑞
LLM投机采样(Speculative Sampling)为何能加速模型推理 Venda
万字综述 10+ 种 LLM 投机采样推理加速方案 AI闲谈
3万字详细解析清华大学最新综述工作:大模型高效推理综述 zenRRan
2401.07851\] Unlocking Efficiency in Large Language Model Inference: A Comprehensive Survey of Speculative Decoding
Stern, Mitchell, Noam Shazeer, and Jakob Uszkoreit. "Blockwise parallel decoding for deep autoregressive models."*Advances in Neural Information Processing Systems*31 (2018)
Xia, Heming, et al. "Unlocking efficiency in large language model inference: A comprehensive survey of speculative decoding."*arXiv preprint arXiv:2401.07851*(2024).
Agrawal, Amey, et al. "Sarathi: Efficient llm inference by piggybacking decodes with chunked prefills."*arXiv preprint arXiv:2308.16369*(2023).
Cai, Tianle, et al. "Medusa: Simple llm inference acceleration framework with multiple decoding heads."*arXiv preprint arXiv:2401.10774*(2024).
Li, Yuhui, et al. "Eagle: Speculative sampling requires rethinking feature uncertainty."*arXiv preprint arXiv:2401.15077*(2024).
Chen, Charlie, et al. "Accelerating large language model decoding with speculative sampling." arXiv preprint arXiv:2302.01318 (2023).
Leviathan, Yaniv, Matan Kalman, and Yossi Matias. "Fast inference from transformers via speculative decoding." International Conference on Machine Learning. PMLR, 2023.
Sun, Ziteng, et al. "Spectr: Fast speculative decoding via optimal transport." Advances in Neural Information Processing Systems 36 (2024).
Miao, Xupeng, et al. "Specinfer: Accelerating generative llm serving with speculative inference and token tree verification." arXiv preprint arXiv:2305.09781 (2023).
Chen, Zhuoming, et al. "Sequoia: Scalable, Robust, and Hardware-aware Speculative Decoding." arXiv preprint arXiv:2402.12374 (2024).