《基于改进Wallace树的Posit乘法单元优化》（一）

原文

文章通过增加特定的计数器、重新设计部分积求和阶段计数器布局

以及改进最终求和阶段使用的加法器，提出一种名为3L-Wallace树的改进Wallace树算法，有效减少了部分积求和的阶段数，

从而降低了硬件资源消耗和整体延迟，然后基于3L-Wallace树对Posit乘法单元进行了优化。此外，文章还引入了模块化设计

方法，将大位数乘法器划分为更易于实现的小模块，简化了设计过程并减轻了实现难度。同时，设计了一种动态选择算法，

根据运行时尾数位宽动态选择合适位宽的乘法器，以避免硬件资源浪费。
原文

已经证明n 位的浮点加法器、乘法器可以安全地被m位Posit 加法器、乘法器取代（m<n）

Klöwer M, Düben P D, Palmer T N. Posits as an alternative to floats for weather and climate models[C]//Proceedings of the conference for next generation arithmetic 2019. 2019: 1-8
原文

相比于IEEE 754 标准，Posit 引入了regime 这一可变字

段，这固有地增加了硬件方面的开销。再加上缺少开

发这种格式的工具，这意味着Posit与IEEE 754格式

相比仍是缺乏竞争力的[9]。前人有关Posit算术单元

的设计和成本的研究[10][11]表明，乘法器和除法器

是能耗最高的算术单元。
原文

乘法器、除法器与IEEE 754 浮点数乘法器的实

现阶段相似，包括操作数的解码、尾数的乘法、指数

部分的计算和结果的编码。尾数乘法器是迄今为止资

源消耗最高的模块，因此，与浮点格式一样，降低尾

数乘法器的复杂度对于优化整个 Posit 乘法单元的功

耗至关重要。

一般乘法的计算过程由两个步骤组成：部分积的

生成和部分积的求和。目前已知提升乘法器性能的方

法，要么减少生成的部分积的数量，要么加速部分积

的求和，也有方法综合了这两种方式。这些方法试图

克服诸如面积、速度和功耗等方面的问题。Dadda树

12\]、Booth 算法\[13\]\[14\]和 Wallace 树\[15\]都是这类设 计的例子，Wallace 树乘法器是最好的并行设计之一， 通过并行地添加部分乘积来减少乘法器的延迟。 原文 乘法运算大致可分为三个阶段：1）使用AND门 阵列生成部分积；2）对部分积进行累加求和；3）对 最终阶段的部分积求和\[22\]\[23\]\[24\]。 传统Wallace树\[25\]通过部分积分组求和的方式 进行运算，在部分积求和的每个阶段，每三行分为一 组，所有部分积分组后仍有一行或两行剩余，则对剩 余的部分不进行处理而是直接传递到下一阶段。前期 所有的阶段都重复这一过程，直至部分积只有两行， 最后使用传统的加法器对这两行进行求和\[26\]。在部 分积求和过程中对分组的处理是使用全加器或半加 器进行求和，从而减少部分积的行数和其中的元素 数。图1以8×8乘法器为例，说明了使用传统Wallace 算法实现的乘法器中部分积求和的过程。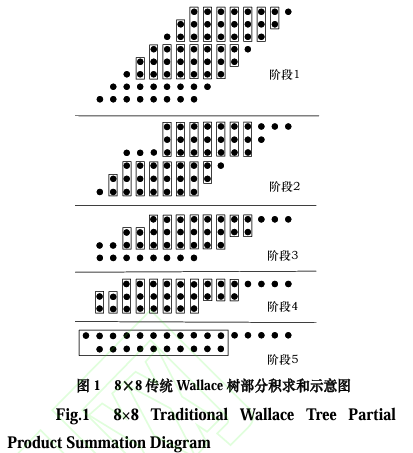 

进位保存加法器（Carry-Save Adder, CSA）详解

---

乘法器------Wallace树型乘法器
Wallace解释

1. 基本概念

进位保存加法器 （Carry-Save Adder, CSA）是一种多操作数加法技术，核心思想是将进位信息保留并传递，而非立即合并，从而减少关键路径延迟。

• 输入：3个二进制数（如部分积的某一位）。
• 输出 ：2个二进制数（和Sum + 进位Carry，其中进位左移1位）。
• 数学表示 ：

  A + B + C = Sum + (Carry \\ll 1)

  （<< 1表示进位左移1位，即乘以2）

---

2. 工作原理

(1) 基本单元：3:2压缩器

• 功能：将3个输入位压缩为2个输出位（1和 + 1进位）。

• 逻辑表达式 ：

  Sum = A \\oplus B \\oplus C \\ Carry = (A \\cdot B) \\mid (B \\cdot C) \\mid (A \\cdot C)

• 电路实现 ：

  A ──┐
      XOR → Sum
  B ──┘
      │
      AND → OR → Carry
  C ──┘

(2) 多级CSA树

• 应用场景：乘法器中的部分积累加（如Wallace树）。

• 示例（4个部分积） ：

  步骤1: CSA1 → A + B + C = S1 + C1
  步骤2: CSA2 → S1 + C1 + D = S2 + C2
  最终：S2 + (C2 << 1) → 输入CPA（进位传递加法器）

---

3. 与传统加法器的对比

特性	进位保存加法器（CSA）	进位传递加法器（CPA）
延迟	O(1) 每级（并行压缩）	O(n)（n为位宽，需进位链传播）
硬件开销	更多压缩器，但无长进位链	较少逻辑，但进位链面积大
适用场景	多操作数累加（如乘法）	两操作数加法

---

4. 在乘法器中的应用（以8×8乘法为例）

(1) 部分积生成

• 8位乘法生成8行部分积（每行最多15位）。

(2) CSA树压缩

• 阶段1：8行 → 6行（使用多个3:2 CSA）。
• 阶段2：6行 → 4行。
• 阶段3：4行 → 3行。
• 阶段4 ：3行 → 2行（和S与进位C）。

(3) 最终相加

• 通过CPA（如Ripple Carry Adder）计算 S + (C << 1)。

---

5. 优势与局限性

优势

• 延迟优化：多操作数加法延迟从O(n)降至O(log n)（树形结构）。
• 并行性：每级CSA可独立处理，适合流水线设计。

局限性

• 最终仍需CPA：CSA仅压缩部分积，最后一步需传统加法器。
• 面积开销：多级CSA需更多逻辑门。

---

6. 硬件实现示例

(1) 单个3:2 CSA单元（Verilog)

module CSA_3to2 (
    input  A, B, C,
    output Sum, Carry
);
    assign Sum   = A ^ B ^ C;
    assign Carry = (A & B) | (B & C) | (A & C);
endmodule

(2) 4:2压缩器（由两个3:2 CSA构成）

CSA1: A + B + C = S1 + C1
CSA2: S1 + D + Cin = S2 + C2
最终：Sum = S2, Carry = C1 | C2

---

7. 扩展应用

• 大数乘法：用于RSA加密中的模幂运算。
• AI加速器：在DNN的乘累加（MAC）单元中压缩部分积。

---

总结

进位保存加法器通过延迟进位合并显著提升了多操作数加法的效率，是高性能乘法器和累加器的核心组件。尽管需配合CPA完成最终计算，但其并行压缩特性使其在硬件设计中不可替代。理解CSA是掌握现代算术逻辑单元（ALU）设计的关键基础。

在数字电路设计（如乘法器或加法树）中，根据输入元素的数量选择全加器（Full Adder, FA）或半加器（Half Adder, HA），主要是为了优化硬件资源的利用和减少不必要的逻辑开销。以下是具体原因分析：

---

1. 全加器与半加器的功能区别

• 半加器（HA） ：
  • 输入：2个二进制位（A、B）。
  • 输出：1位和（Sum）和1位进位（Carry）。
  • 局限性：无法处理来自低位的进位（即仅支持两数相加，无进位输入）。
• 全加器（FA） ：
  • 输入：3个二进制位（A、B + 低位进位Cin）。
  • 输出：1位和（Sum）和1位进位（Carry）。
  • 灵活性：可级联形成多比特加法器（如行波进位加法器）。

---

2. 为什么区分使用？

（1）资源效率

• 三元素列 ：
  当需要将3个二进制数 相加时（例如乘法器的部分积压缩阶段），必须使用全加器，因为需要处理两个数的和加上前一级的进位 （共3个输入）。
  • 例子：在Wallace树或Dadda树乘法器中，每列可能有多个部分积累加，全加器可高效压缩3个输入为1个和和1个进位。
• 双元素列 ：
  若某列仅有2个二进制数 相加（无进位输入），使用半加器即可完成任务，无需浪费全加器的第三个输入端口。
  • 节省资源：半加器比全加器少一个逻辑门（通常少一个异或门或与门），在大规模电路中可显著减少面积和功耗。

（2）避免冗余逻辑

• 若对双元素列强制使用全加器，其第三个输入（Cin）需固定为0，导致：
  • 多余的逻辑门计算（如Cin=0的与门运算）浪费功耗。
  • 电路复杂度增加，时序可能劣化（尽管现代综合工具可能优化掉无效逻辑）。

（3）设计清晰性

• 区分使用HA和FA可使电路结构更直观，便于工程师理解和验证。例如：
  • 乘法器部分积压缩：明确标注哪些列需FA（3输入）或HA（2输入），简化布局布线。

---

3. 实际应用场景

以无符号乘法器为例：

1. 生成部分积：乘数的每一位与被乘数相与，产生多个部分积。
2. 压缩部分积 ：
   • 对每列的比特数统计：
     • 若某列有3个1，使用全加器将其压缩为1个和（Sum）和1个进位（Carry至高位）。
     • 若某列仅有2个1，使用半加器压缩为1个和和1个进位。
   • 最终通过加法器链（如超前进位加法器）输出结果。

---

4. 现代优化技术

• 工具自动化 ：
  现代EDA工具（如Synopsys Design Compiler）可自动识别输入数量，选择HA或FA，甚至替换为更优化的复合单元（如4:2压缩器）。
• 近似计算 ：
  某些场景（如AI加速器）可能直接忽略低权重进位，进一步简化逻辑。

---

总结

区分使用全加器和半加器的本质是匹配输入需求与硬件资源：

• 全加器处理3输入列的复杂情况，保留进位链的完整性。
• 半加器 处理2输入列的简单情况，节省面积和功耗。
  这种设计在乘法器、加法树等高频模块中尤为重要，直接影响了电路的性能、功耗和面积（PPA）。

原文

RCA的基本工作原理是通过一系列的全加器

（full adders）来逐位计算两个二进制数的和。每个

全加器负责处理一个位的加法，并处理来自低位的进

位。

行波进位加法器（Ripple Carry Adder, RCA） 是最基础的二进制加法器结构，它通过级联全加器（Full Adder, FA） 逐位计算两个二进制数的和，并处理进位传递。以下是其详细工作原理和特点分析：

---

1. RCA 的基本结构

• 输入：两个 N 位二进制数 ( A ) 和 ( B )（如 ( A = A_{N-1}A_{N-2}...A_0 ), ( B = B_{N-1}B_{N-2}...B_0 )）。
• 输出：N 位和 ( S ) 和 1 位最终进位 ( C_{\text{out}} )。
• 组成 ：
  • N 个全加器（FA） 级联，每个 FA 处理 1 位加法。
  • 进位链：低位的进位输出（( C_{\text{out}} )）连接到高位的进位输入（( C_{\text{in}} )）。

---

2. 全加器（FA）的功能

每个全加器的逻辑如下：

• 输入：( A_i ), ( B_i ), ( C_{\text{in}} )（来自低位的进位）。
• 输出 ：
  • 和位（( S_i )：( S_i = A_i \oplus B_i \oplus C_{\text{in}} )（异或运算）。
  • 进位位（( C_{\text{out}} ) ：( C_{\text{out}} = (A_i & B_i) \mid (B_i & C_{\text{in}}) \mid (A_i & C_{\text{in}}) )。
    • 即：若至少有两个输入为 1，则进位为 1。

---

3. RCA 的工作流程

以 4 位 RCA 为例（计算 ( A + B )）：

1. 最低位（LSB, ( i=0 \） ：
   • ( C_{\text{in}} = 0 )（无前级进位）。
   • 计算 ( S_0 = A_0 \oplus B_0 \oplus 0 )，( C_{\text{out}} ) 传递到 ( i=1 )。
2. 中间位（( i=1, 2 )） ：
   • ( C_{\text{in}} ) 来自前一级的 ( C_{\text{out}} )。
   • 计算 ( S_i = A_i \oplus B_i \oplus C_{\text{in}} )，并生成新的 ( C_{\text{out}} )。
3. 最高位（MSB, ( i=3 \） ：
   • 计算 ( S_3 ) 和最终的 ( C_{\text{out}} )（即溢出标志）。

---

4. RCA 的特点

优点

• 结构简单：易于理解和实现，仅需级联全加器。
• 面积小：硬件资源消耗少（适合低功耗或面积受限场景）。

缺点

• 速度慢 ：
  • 进位信号必须从最低位逐级传递到最高位（行波效应）。
  • 关键路径延迟 = ( N \times T_{\text{FA}} )（( T_{\text{FA}} ) 为全加器延迟）。
  • 例如，32 位 RCA 的延迟是 16 位 RCA 的两倍。

---

5. RCA 的关键问题：进位延迟

• 进位传播（Carry Propagation） 是 RCA 的主要瓶颈。
  • 最坏情况下，进位需经过所有 N 级全加器（如 ( 111...1 + 000...1 )）。
• 优化方法 ：
  • 超前进位加法器（CLA）：提前计算进位，减少延迟。
  • 进位选择加法器（CSA）：并行计算不同进位路径。
  • 进位旁路加法器（Carry-Skip）：在特定条件下跳过部分进位链。

---

6. RCA 的应用场景

• 低位数加法（如 4~8 位）：延迟可接受。
• 教学与原型设计：便于理解加法器基本原理。
• 作为子模块：更复杂加法器（如分段 RCA + CLA）的基础。

---

7. 示例：4 位 RCA 计算 ( 1101 + 1011 )

位	( A_i )	( B_i )	( C_{\text{in}} )	( S_i )	( C_{\text{out}} )
0	1	1	0	0	1
1	0	1	1	0	1
2	1	0	1	0	1
3	1	1	1	1	1

• 结果：( S = 1000 )，( C_{\text{out}} = 1 )（溢出，实际和为 ( 11000 )）。

---

8. 总结

• RCA 是串行进位的加法器，简单但速度慢。
• 关键改进方向：优化进位链（如 CLA、CSA、Carry-Skip）。
• 现代应用：通常仅用于低位数加法或作为更高效加法器的组成部分。

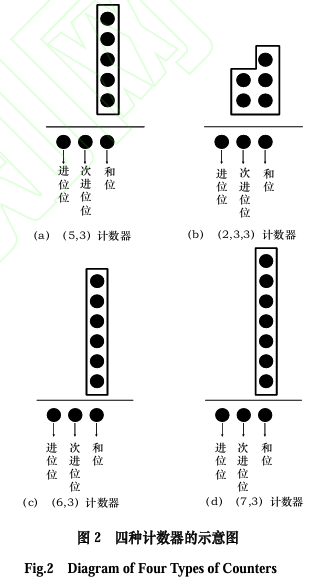
加法器能够产生次进位（也称为低位进位或传递进位）的原因在于其设计和工作原理。让我们详细解释这一点：

1.加法器的基本工作原理

加法器是数字电路中的基本组件，用于执行二进制加法。它通过组合逻辑电路计算两个二进制数的和以及可能的进位。

• 全加器（Full Adder） ：全加器是加法器的基本单元，用于计算三个输入位（两个加数位和一个来自低位的进位）的和。它有两个输出：
  • 和（Sum）：表示当前位的加法结果。
  • 进位输出（Carry Out）：表示向高位的进位。

全加器的逻辑表达式为：

\\text{Sum} = A \\oplus B \\oplus C_{\\text{in}}

C_{\\text{out}} = (A \\land B) \\lor (A \\land C_{\\text{in}}) \\lor (B \\land C_{\\text{in}})

其中：

• (A) 和 (B) 是当前位的两个加数。
• (C_{\text{in}}) 是来自低位的进位输入。
• (C_{\text{out}}) 是向高位的进位输出。

2.次进位的产生

在多个全加器级联组成多位加法器时，每个全加器的进位输出 (C_{\text{out}}) 会传递给下一个高位全加器的进位输入 (C_{\text{in}})。这个传递的进位信号就是次进位。

• 次进位的定义：次进位是指从低位全加器传递到当前全加器的进位信号。它表示低位的加法操作是否产生了需要传递到当前位的进位。
• 次进位的作用：次进位用于控制当前全加器的进位输出计算。只有当次进位有效时，当前全加器才会考虑来自低位的进位输入。

3.次进位在加法器中的传递

在多位加法器中，次进位从最低位开始逐位传递到高位。例如，在一个4位加法器中：

• 第一位全加器的进位输入 (C_{\text{in}}) 来自外部（通常为0或1）。
• 第一位全加器的进位输出 (C_{\text{out}}) 成为第二位全加器的进位输入 (C_{\text{in}})。
• 第二位全加器的进位输出 (C_{\text{out}}) 成为第三位全加器的进位输入 (C_{\text{in}})。
• 依此类推，直到最高位。

4.次进位与进位的关系

• 进位输入（(C_{\text{in}})）：是当前全加器从低位接收到的进位信号，即次进位。
• 进位输出（(C_{\text{out}})）：是当前全加器计算出的进位信号，将传递给高位全加器。

通过次进位的传递，加法器能够正确地处理多位数的加法运算，并确保每一位的加法结果和进位输出正确。

总结

加法器能够产生次进位的原因在于其内部的全加器结构和进位传递机制。每个全加器根据输入的加数位和来自低位的次进位计算当前位的和以及进位输出。次进位的传递使得多位加法器能够正确地处理多位数的加法运算。