最近，DeepSeek-R1 和 OpenAI o1/03 等推理大模型在后训练阶段探索了长度扩展（length scaling），通过强化学习（比如 PPO、GPRO）训练模型生成很长的推理链（CoT），并在奥数等高难度推理任务上取得了显著的效果提升。
受此启发，研究人员开始探索预训练阶段的长度扩展，已有方法包括在序列中插入文本、插入潜在向量（如 Coconut）、复用中间层隐藏状态（如 CoTFormer）以及将中间隐藏状态映射为概念（如 COCOMix）。不过，这些方法普遍存在问题，比如需要更大的 KV 缓存导致推理慢 / 占内存多。
本文中，来自 ByteDance Seed 团队的研究者提出了更简单的方法：直接重复输入 tokens（1/2/3/4 次），不做中间层处理。他们观察到了训练损失和模型性能随重复倍数扩展的趋势，如下图 1a 和 1b 所示。但是，直接重复 tokens 也带来了新问题，包括 KV 缓存规模线性增加，内存压力大；预填充时间超线性增加；解码延迟变长。这些都是实现预训练长度扩展需要重点解决的挑战。
-
论文标题：Efficient Pretraining Length Scaling
-
arXiv 地址：arxiv.org/pdf/2504.14...
研究者提出了一种推理友好的新颖长度扩展方法，核心是 PHD-Transformer（Parallel Hidden Decoding Transformer），它保持了与原始 transformer 相同的 KV 缓存大小，同时实现有效的长度扩展。PHD-Transformer 通过创新的 KV 缓存管理策略实现了这些能力。
具体来讲，研究者将第一个 token 表示原始 token，将重复的 token 表示为解码 token。同时仅保留从原始 token 生成的 KV 缓存来用于长距离依赖建模，并在隐藏解码 token 用于下一个 token 预测之后丢弃它们的 KV 缓存。因此，PHD-Transformer 提供了与原始 transformer 相同的 KV 缓存，同时相较于简单的 token 重复实现了显著的推理加速（如图 1d 所示）。
另外，为了更好地保留隐藏解码 token 的 KV 缓存的性能优势，研究者引入了一种滑动窗口注意力 ------PHD-SWA，保持了这些 token 的局部滑动窗口缓存，在实现显著性能提升的同时，仅需要
的额外 KV 缓存内存。
研究者还注意到，在 PHD-SWA 中，隐藏解码 token 的 KV 缓存表现出了顺序依赖关系，这导致预填充时间呈线性增长。为了解决这个问题，研究者提出了逐块滑动窗口注意力 ------ PHD-CSWA，从而限制了每个块内的顺序依赖关系。
因此，得益于只有最后一个块的预填充时间呈线性增长，PHD-CSWA 显著缩短了预填充时间（如图 1c 所示）。
方法概览
PHD 的架构下图 2 所示，与原始 Transformer 相比，PHD 保留了相同的模型架构，仅在输入序列和注意力矩阵的设计上有所不同。具体而言，他们仅允许原始 token
生成 KV 缓存，并且可以被所有 token 全局关注；同时隐藏状态的 KV 缓存在并行隐藏解码后会被立即丢弃。注意力矩阵的策略具体如下：
研究者在推理过程中实现了与原始 Transformer 相同的 KV 缓存大小和内存访问模式。虽然需要 K 次 FLOP，但这些计算可以并行处理，从而在内存受限的推理场景中最大限度地降低延迟开销。该架构的核心优势在于原始 token 和隐藏解码 token 之间的解耦。在预填充期间，只有原始 token 需要计算。
这种设计确保预填充时间与原始 Transformer 相同，并且无论扩展因子 K 如何变化，预填充时间都保持不变。而对于损失计算，研究者仅使用 token 的最终副本进行下一个 token 的预测。总之，使用 token 的第一个副本进行 KV 缓存生成，使用 token 的最后一个副本进行下一个 token 的预测。
内核设计
M^ij_mn 的简单实现会导致注意力层计算量增加 K^2 倍，FFN 层计算量也增加 K 倍。然而，由于注意力是稀疏计算的，
的注意力可以大幅降低。因此，研究者将原始 token 和隐藏解码 token 分成两组，并将它们连接在一起。
下图 3 展示了 K = 3 的示例，可以得到一个包含 t 个原始 token 的序列和一个包含 2t 个隐藏解码序列的序列。通过重新排列 token 的位置，研究者将掩码注意力的位置保留在一个连续块中，从而优化了注意力计算，将注意力计算复杂度降低到
。
PHD-SWA 和 PHD-CSWA
与简单的 token 重复相比，PHD-Transformer 在保持原始 KV 缓存大小的同时实现了长度扩展。然而通过经验观察到，为隐藏解码 token 保留一些 KV 缓存可以带来显著的性能提升。因此，为了在保持效率的同时获得这些优势，研究者引入了 PHD-SWA，将滑动窗口注意力限制在 W 个先前的隐藏解码 token 上。
如下图 4 所示，PHD-SWA 的注意力模式将对原始 token 的全局访问与对 W 个最近隐藏解码 token 的局部访问相结合。这种改进的注意力机制实现了显著的性能提升，同时仅需要的额外 KV 缓存内存。
虽然 PHD-SWA 滑动窗口方法提升了模型性能，但由于隐藏解码 token 的 KV 缓存中存在顺序依赖关系，它会产生 K 倍的预填充开销。为了解决这个问题，研究者引入了 PHD-CSWA，它可以在独立的块内处理注意力。
如下图 4 所示，PHD-CSWA 将滑动窗口注意力限制在单个块内运行。这种架构创新将额外的预填充开销减少到最终块内的 K 次重复，而不是整个序列重复，这使得额外的计算成本几乎可以忽略不计，同时保留了局部注意力模式的优势。
实验结果
在实验中，研究者使用 OLMo2 作为代码库，并在 ARC、HellaSwag、PIQA、Winogrande、MMLU 和 CommonsenseQA 等公开基准测试集上进行了评估。
训练细节：研究者使用 1.2B 参数规模的模型，它是一个 16 层的密集模型。每个 token 的隐藏层维数设置为 2048，FFN 层的隐藏层大小设置为 16384。同时使用组查询注意力 (Group-Query Attention，GQA)，它包含 32 个查询头和 8 个键 / 值头，每个头的隐藏层维数设置为 64。研究者使用 500B 个 token 训练该模型。
对于本文提出的 PHD 系列设置，研究者预训练了以下两种 PHD-CSWA 变体：
-
PHD-CSWA-2-16-32，其中训练 token 重复两次。保留一个包含 16 个 token 的局部窗口，并将块大小设置为 32 个 token。
-
PHD-CSWA-3-16-32，其中训练 token 重复三次。局部窗口大小和块大小与 PHD-CSWA-2-16-32 的设置相同。
PHD-CSWA 在各个基准测试中均实现了持续的性能提升。下图 5 中展示了训练曲线，下表 1 中展示了主要结果。本文提出的 PHD-CSWA-2-16-32 在这些基准测试中平均实现了 1.5% 的准确率提升，训练损失降低了 0.025；而 PHD-CSWA-3-16-32 在这些基准测试中平均实现了 2.0% 的准确率提升，训练损失降低了 0.034。
研究者还分析了 PHD 和 PHD-SWA 的扩展性能，以分析扩展解码计算的性能。 训练细节：使用相同的 550M 模型配置，将窗口大小 W 设置为 16，并在 {2, 3, 5} 范围内改变扩展因子 K。对于局部窗口大小，研究者在所有实验中都将窗口大小设置为 16。
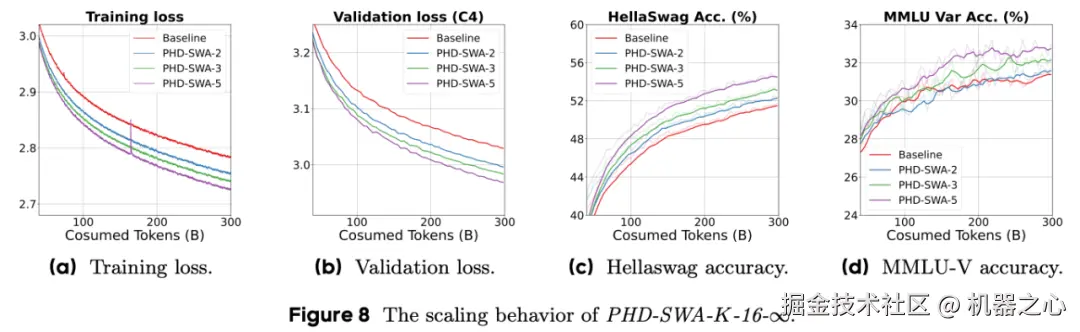
PHD-SWA 的性能在增加扩展因子时有效扩展。如下图 8 所示，使用固定窗口大小时，损失曲线和下游性能会随着 token 重复次数而有效扩展。通过将扩展因子设置为 5，可以实现接近 0.06 的损失降低，同时显著提升下游性能。
下表 2 中的定量结果表明，当扩展至 K = 5 时，所有基准测试的平均准确率提高了 1.8%，这证实了本文的方法在更激进的扩展方面仍然有效。
更多实验结果请参阅原论文。