对于下面的系统,可以凭直觉看出:通过控制量u可以控制状态x1,x1_dot;

图1 系统1
那如果对上述系统1加一个拖挂,变为系统2:
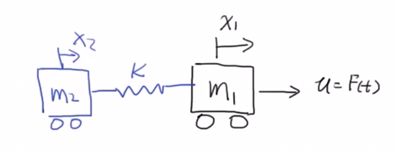
图2 系统2
是否通过控制量u可以控制状态x1,x1_dot;x2,x2_dot?这有点难,也引出了系统可控性的判断问题。
可控性的定义:
对于线性时不变系统,系统的可控性指是否存在一系列控制量,使得系统可以从t0的状态a转移到t1的状态B;

具体可控性的判断公式,可用离散型系统推导得到:

上述xn的表达式中,记:

下面,我们看一个具体的例子,可以看出这个系统不可控:

再看另一个例子,可以得出系统是可控的:

图3 系统3
可控性是点对点的可控,还是轨迹上的可控?
以图3系统为例,其从x0到达xt,相轨迹如下图所示,可见无法从初始状态以随便的状态轨迹到终端状态;

故可控是点到点上的可控(肯定可以找到一个状态转移轨迹),不是轨迹上的可控。
再回到图2,这个增加了悬挂的系统;进行系统建模,如下:
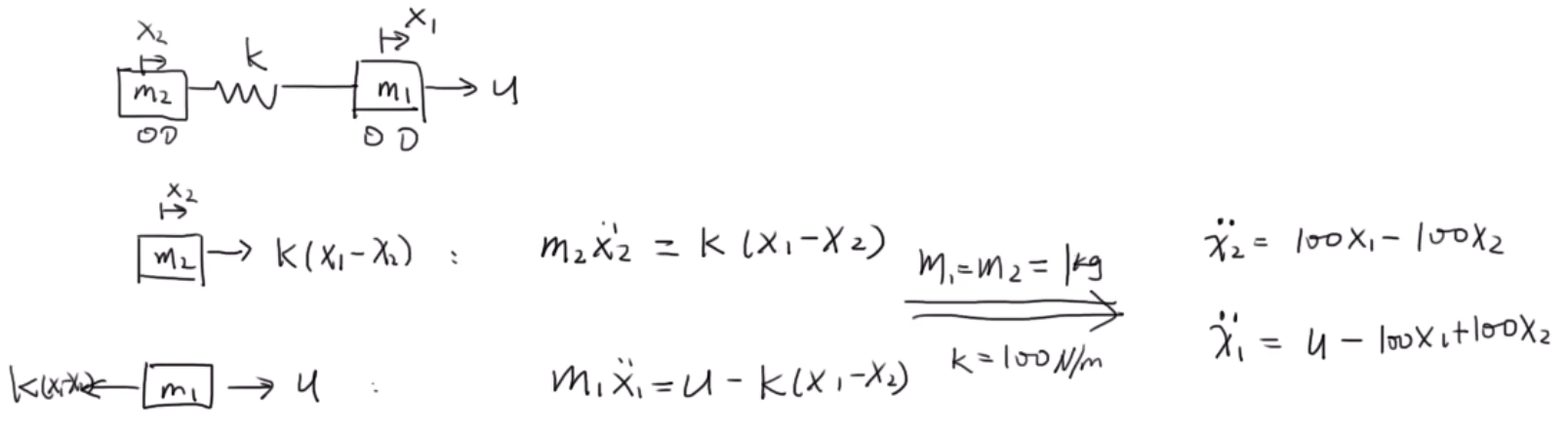

可得到rank(c0)=4,所以系统是可控的。
最后总结:
