一篇文章给你讲清楚运筹优化到底怎么学！基于 SCIP Optimization Suite 的运筹优化入坑教程

多玩我的世界盒子2025-05-19 18:18

!abstract

本文笔者用暴躁而又不失严谨性的语言，从优化问题的背景入手，强调了针对实际的工程问题开展的优化建模方法和学校教学内容之间的偏差，并围绕优化建模到底应该怎么学的问题，讲解了如何下载和安装通用求解器、如何通过 Zimpl 规划建模语言编写模型定义并在求解器中求解。

目录

前言

促使我写这篇文章的原因呢，是因为这段时间开始我一直在写我的毕业论文。在写毕业论文的时候，我就用到了一些运筹优化方法，与此同时我也在观察身边人是如何运用运筹优化方法的。在这个过程中，我就逐渐开始意识到一件事情，那就是：学校其实从来没有教过我们如何搞运筹优化。

我想即使是现在在阅读本文的你，也不得不承认：学校教运筹学的方法就是拿着课本，把所有典型的运筹学问题及数学表述和其求解的算法形式照本宣科地讲一遍，事后再给你安排一场考试，让你在考场上手工迭一遍单纯形表、迭一遍运输表、求一个对偶问题、算一步灵敏度分析，用 Dijkstra 算法找一下两点之间的最短路径云云。说好听点，这些都是运筹学中的基本内容；说难听点，你一个学期的课跟六个小时的猴博士期末不挂科视频没有半毛钱区别。

如果你整个课程的设计目的从一开始就是为了考研服务的，或者说，仅仅是为了点"运筹学"这个课题，拓展一下学生思维，那你这个课程安排可能确实没什么毛病对吧。

但是不要忘了：学生学运筹学的目的是要运用运筹优化方法，解决科研或工程建设中的实际问题的。学校你既然这样教运筹学，好家伙，考试的时候身边的同学一个个考的分都比我高，结果到了打数学建模竞赛的时候，找几个有战斗力的队友比TM大海捞针都难。

为了从彻底上解决问题，我觉得我有必要写这样一篇文章。这篇文章并不只在教会运筹优化方法，而是给你厘清楚"搞运筹优化到底是在搞什么"这样一个简单的问题，以便于你后续能自主学习。我也希望在我写完这篇文章之后任何一个数模运筹手都不要再被找队友这样的事情折磨。

!note

本文的内容主要是面向大学本科生或者研 0 生的，适合刚刚学完学校开设的运筹学课程却又对很多问题感到一头雾水、不明白学校为什么要教那么多没用的东西的新人入门看。如果你已经是研究生了，那本文的内容可能对你的学习或者工作太过浅显。建议你先快速翻翻看本文下面的内容，斟酌一下要不要继续看下去。

什么是优化问题

常见优化问题形式

运筹优化，或者叫运筹学规划问题，这两种称呼在本文中就不做区分了，其实是一个意思。首先我们在这里简单带读者快速过一遍三种常见的优化问题：线性整数规划、非线性整数规划还有混合 0-1 整数规划这三种典型的形式。我们别的不看，只看三个问题最基本的形式。首先是线性规划模型：

!example\] 线性整数规划问题 假设现在有一座工厂生产 A、B 两种产品，A 产品消耗 2 块钢板，能卖 3 万块钱，B 产品消耗 4 块钢板，能卖 5 万块钱。我们规定 A 产品最多生产 30 件，不然工厂就会爆炸。问你工厂各生产多少 A 产品、多少 B 产品，能赚最多的钱？ 针对这个问题，我们设我们要生产 \\(x_1\\) 份 A 产品、\\(x_2\\) 份 B 产品，则问题的形式可以表示为如下的形式： \\\[\\begin{aligned} \\text{Maximize } \& f\^\* = 3x_1 + 5x_2 \\\\ \\text{Subject to } \& 2x_1 + 4x_2 \\leq 100 \\\\ \& x_1 \\leq 30 \\\\ \& x_1, x_2 \\in \\mathcal{N} \\end{aligned}\\tag{1} \\

其中，\(\text{Subject to}\) 后面紧随的等式或不等式形式称为规划模型的约束，\(f^* = 3x_1 + 5x_2\) 为模型的目标函数，\(\mathcal{N}\) 代表全体自然数的集合。这个模型的意思就是说：我们要在满足后面的约束条件的前提下，求出 \(f^* = 3x_1 + 5x_2\) 的最大值。

如果你已经学过了一些运筹学的知识，你就会知道这个优化模型可以通过分支定界单纯形法来求解。但是我想请读者们先把这件事情忘掉，如果你没学过，那就正好，你就干脆甭管了。现在不要关心这个模型怎么求解。我们先关注两个简单的事实，那便是：(1) 我们有办法把这个模型求解出来；(2) 只要我们将这个模型求解出来，就能得到我们想要的结果。请读者们记住这个结论！

跟着我一起继续往下，我们来看一个非线性整数规划的模型的例子。还是这个工厂：

!example\] 非线性规划问题 假如说由于我们这个工厂的 A 产品在中东卖得太好了，造成了很大的国际问题，客户所在国的政府要给你的产品加关税。这个关税的机制是要从你的收入中扣掉价值相当于 A 产品销售额乘以销售数量的 1%，也就是 \\(0.3 x_1\^2\\)。这种种情况下，我们就要修改上面的线性模型，变成： \\\[\\begin{aligned} \\text{Maximize } \& f\^\* = 3x_1 + 5x_2 - 0.03 x_1\^2\\\\ \\text{Subject to } \& 2x_1 + 4x_2 \\leq 100 \\\\ \& x_1 \\leq 30 \\\\ \& x_1, x_2 \\in \\mathcal{N} \\end{aligned}\\tag{2} \\

由于数学公式里带了个平方，不再是线性方程的形式，因此这种模型就被称为非线性模型。

接下来再看一个非线性混合 0-1 整数规划模型的例子。依然是这个工厂：

!example\] 非线性混合 0-1 整数规划问题 我们假设现在因为我们的工厂经营得太好了，马斯克让我们给他造个星舰。这个星舰造一个就要消耗 50 块钢板，但是造成了之后，马斯克许诺一次性给我们 75 万。我们这个时候可以把星舰设为变量 \\(x_3\\)。星舰要么不造，要么就造一艘，所以 \\(x_3\\) 的值只能是 0 或者 1。这个时候，我们可以把我们的模型形式改为： \\\[\\begin{aligned} \\text{Maximize } \& f\^\* = 3x_1 + 5x_2 + 75 x_3 - 0.03 x_1\^2\\\\ \\text{Subject to } \& 2x_1 + 4x_2 \\leq 100 \\\\ \& x_1 \\leq 30 \\\\ \& x_1, x_2 \\in \\mathcal{N}, x_3 \\in \\{0, 1\\} \\end{aligned}\\tag{3} \\

由于模型的形式当中混合了 0-1 规划和非线性的方程形式，所以我们将这个问题形式称之为非现象混合 0-1 整数规划问题。

从上面三个典型的问题形式，我们可以总结出这样的一个结论：所谓的优化问题，就是我们针对一个实际的问题形式，写出：

  1. 我们要优化的一个极大或极小化的方程式 \(\max f\) 或者 \(\min f\)，称为目标函数；
  2. 一些未知数 \(X\)，称为决策变量；
  3. 有的时候会有一些对 \(X\) 的取值的限制条件，称为模型约束。

然后用一些方式将 \(X\) 和 \(f\) 的具体取值算出来。

对于我们这个工厂而言，不管我们现在要增加一种什么样的产品，只要我们确定这个产品能挣多少钱、知道这个产品要消耗多少钢板，我们就可以通过给这个模型增加更多约束或者更多变量的方式，根据实际情况，无限拓展下去。我们想怎么写就能怎么写，想怎么定义就能怎么定义。说到底，无非是搞到最后模型有多复杂的问题------这会影响我们模型的求解的难易程度，但可以肯定是，只要模型能够被求解出来，我们就能获得我们想要的答案。这个时候你一定会有疑问，那么既然这样的话，这些模型该如何求解呢？

现在我可以明确告诉你，作为一个工科专业的学生，如何求解这些模型根本不是你马上需要关心的问题。至于为什么，让我后面慢慢跟你说。

优化问题的形式的数学表述

这里先让我把我们刚才已经得出的结论用严谨的数学语言表述一下。

!note

如果你看不懂这个章节到底在说什么，那就不要看了。因为这个章节放在这里并不是给所有读者看的，主要作用只是为了证明笔者确实查了很多的资料还研究了数学，证明本文是严谨的博客文章，而不是在乱写。不过如果你发现自己确实能看懂，那你其实不妨看一看。

数学规划问题，也称优化问题，是运筹学下的一个重要分支，是指在一定约束条件下，最大化或最小化某一目标函数的问题。其变量可能是连续或离散的，其目标函数和约束的形式可能是线性或非线性的。基础的数学规划形式包括线性规划、动态规划、混合 0-1 整数规划等。如下的定义阐释了一个运筹优化模型的数学表述。

!definition\] 优化问题 一个典型的运筹学优化问题可以被定义为 \\(P = (S, f)\\) 的模型形式。其中包括： * \\(X = \\{x_1, x_2, \\cdots, x_n\\}\\) 为模型的决策变量； * \\(D_1, D_2, \\cdots, D_n\\) 为各决策变量的值域； * 决策变量之间的约束形式，通常表现为一系列等式和不等式的集合，我们用 \\(C\\) 表示； * 极小化^[\[1\]](#[1])^目标函数 \\(f\\)，\\(f: D_1 \\times D_2 \\times \\cdots \\times D_n \\rightarrow IR\^+\\)。 在此基础之上，\\(X\\) 完整的取值范围可以被表述为如下式所示的形式： \\\[S = \\{ s \\vert s = \\{(x_1, v_1), (x_2, v_2), \\cdots, (x_n, v_n)\\} \\vert v_i \\in D_i, s \\models \\forall c \\in C \\} \\tag{4} \\

这里的集合 \(S\) 我们一般称之为优化问题的解空间，或者在求解模型的时候也叫搜索空间。其中的每一个元素 \(s\) 均符合所有约束定义，都是这个模型的一个可行解。而求解运筹优化模型，实际上就是获取全局最优解的值或其近似值的过程。

!definition\] 全局最优解 对于一个优化问题 \\(P = (S, f)\\)，\\(\\exists s\^\*\\) 使 \\(f(s\^\*)\\) 满足 \\(f(s\^\*) \\ge f(s), \\forall s \\in S\\) 恒成立，则称 \\(s\^\*\\) 是 \\(P\\) 的一个全局最优解。

搞运筹优化到底是在搞什么

非典型问题

在本节中，我首先得跟读者强调一件事情，那就是对于工科生来说，典型问题的典型求解方法根本不重要。

学校教我们运筹优化的时候，讲的内容大部分是运筹学基础中的典型问题的形式，比如什么线性规划、对偶问题、运输问题、指派问题、能够通过分支定界，方法求解的整数规划问题、动态规划问题、最小生成树问题、最短路径问题、旅行商问题、最小费用流问题、最大流问题、统筹问题等等。虽然说这些典型的问题形式已经被学界研究了很多年，大部分都已经有了非常成熟的求解算法。

学校你既然这么教，好，那我问你，来你告诉我在正常情况下学生遇到一个具体的工程问题的形式恰好就相当于是典型问题形式的概率有多大，你告诉我？Look in my eyes！

我们就拿前文的那个钢铁厂为例，想象你按照学校教的对吧，辛辛苦苦地将厂里的每一种钢铁产品都设成了规划变量 \(x_1\) 到 \(x_n\)，然后按照学校教的，写好了模型的代码，用 MATLAB 的 intlinprog() 函数求解。结果你的客户所在国对你的一种或几种产品征收了一个按非线性因式计算的税，或者老马跟你说他只需要一条星舰，你造两条他就不买了，那你的线性整数规划直接就变成了非线性整数规划，或者变成了混合 0-1 规划，那你写的代码就废了啊！那就要从头写，还要自己设计求解算法。那你这不是折磨人吗？

我也不是说工科生就完全不需要关注这些典型问题的求解算法对吧，这些求解算法当然可以学，但是工科生学习这些算法的重点应该放在：了解这些算法的设计者究竟是如何考虑的；了解为什么要这样设计算法，以及这些算法是如何工作、如何实现其功能的，而不是------像学校现在考试要求的那样------将这些算法的迭代过程背下来、记下来，甚至是拿着纸和笔手工去算。这有什么用呢？

特定领域建模的专业性

在我们现实世界中的很多问题实际上都可以被转化为数学规化的形式去解决。甚至，有些问题的形式虽然乍一看和某种特定的规划没有任何关系，实际上在建模者拥有一定的专业技术知识之后，就会发现这些问题仍然类似于已知的某种典型模型的形式，或者在典型问题的基础上扩展了变量和约束形式。然而，发现这些实际问题和其背后的典型模型之间的联系，需要特定领域的经验和专业知识。比如：

  • 在交通领域，工厂配送中心和客户之间的运输分配可以被转化为各类车辆路径问题及其在各种约束条件下的变体形式。但是这需要工程师了解货物在配送过程中，客户的具体需求、运输装备、库存设施和运输器材的局限性。
  • 在网络工程领域，网络带宽的动态分配问题可以被转化为图论优化的形式，但是这需要工程师了解无线信道特性、网络切片隔离机制这样的网络知识。
  • 在医学领域，急诊科室的床位与医护人员的动态资源调配应对患者到达的不确定性的问题可以被转化为调度系统优化，但是这需要工程师了解急诊流程、患者的分配规则和医护人员的排班法则。
  • ......

然而，另一方面，将这些模型求解出来，需要的是坚实的数学和算法基础。这就需要工程师了解内点算法，了解元启发，懂得计算机执行数值运算程序的底层原理，要懂得如何设计求解和改进算法，从而降低算法的复杂度。

显然，研究某一特定领域专业知识的人和纯粹研究运筹优化的数学理论的人不可能总是共享所有的知识。我们既不可能指望一个天天在田间地头插拔传感器的农业自动灌溉系统的优化工程师对着复杂的数学形式证明指手画脚地推导，也不可能指望一个成日在理论领域埋头苦干的数学家去做客户满意度调查来研究如何确定货物送达的时间窗口。

规划建模的分工化

其实，早在几十年前，早在商业化的大型通用求解器诞生以前，对于那些特别复杂的、包含大量约束和变量定义形式的模型，建模者可能真的必须自己用电脑把求解模型的代码实现一遍。在当时，运筹学规划建模的成本之高、难度之大可想而知。

然而，就像人类历史上一切生产活动的发展那样，在数学规划建模领域出现了分工。就好比网页设计领域的前端和后端那样，在数学规划领域当中，交通、电力、机械、设计领域的工程师们通过自己的专业技术，将特定的具体问题转化为数学模型，用数学公式阐述模型的定义，而数学家和计算机算法专家们则设计出威力强大的求解器，求解这些模型。

这种工程领域的分工带来了许多优势。一方面，由于用于求解模型的算法被封装在求解器内部，而求解器又能够应对多种不同的模型形式，因此求解算法得以在不同模型之间迁移。人们不再需要针对不同的模型反复编写代码。通过将求解算法与模型定义相分离，降低的建模求解的成本和难度 。另一方面，模型的设计者在设计模型的时候并不需要在模型的求解算法上下太多的功夫，相反，他们可以把主要的精力集中于具体问题的需求和模型的数学形式，而他们所关注的内容，也可以在更大程度上倾向于：如何将具体的、现实的确切需求转化为数学表述的形式。比起典型问题和典型的求解算法，这些才是工科生在实际学习运筹优化的过程当中，更应该关心的要点。

规划模型描述语言

什么是规划模型描述语言

在优化建模领域分工的大背景下，规划建模描述语言就应运而生了。本文的读者有些可能用过 LINGO，LINGO 就是一种典型的规划建模描述语言。

简单来说，当我们在写完模型的数学公式之后，计算机并不能直接读懂我们写在纸面上的数学符号和数学公式 。为此，我们需要一些方式，将这些数学公式表达为计算机能读懂的语言，从而让求解器能够读取、分析，在计算机中构建模型实例，然后运行算法迭代，最后输出我们想要的结果。规划建模与研究像是一座连接数学公式与计算机的桥梁。

虽然本文中所称的"规划模型描述语言"和"编程语言"英文都叫 Programming Language[[2]](#[2])，但两者是截然不同的东西。前者包含对一些过程的定义，需要计算机在读取之后，按照代码的指示，一步一步地"照做下去"，而后者是一种 DSL (Domain-Specific Language，即特定领域语言)，仅仅只是纸面上的数学公式在计算机中的另一种表述形式，只不过它能被计算机读取和理解。从某个角度上来说，规划建模语言"长得越像数学公式越好"------关于这件事，在本文下文中具体讲到"数学规划建模语言怎么写"的问题上的时候会有更加详细的解释。

规划建模语言的小例子

我们这里为了给读者一个比较直观的概念，用一种名为 Zimpl 的规划模型描述语言写一下我们前面的那个钢铁厂的例子。本文下文中的大部分讲解也会主要使用 Zimpl 语言。这是一种小众但是十分好用的运筹优化建模语言，关于这种语言，本文后文会和读者们详细介绍的。读者们现在应该记得，我们前文给出的钢铁厂模型的形式如本文式 (3) 所示。我这里再写一遍：

\[\begin{aligned} \text{Maximize } & f^* = 3x_1 + 5x_2 + 75 x_3 - 0.03 x_1^2\\ \text{Subject to } & 2x_1 + 4x_2 \leq 100 \\ & x_1 \leq 30 \\ & x_1, x_2 \in \mathcal{N}, x_3 \in \{0, 1\} \end{aligned}\tag{5} \]

如果我们将式 (5) 所述的模型写在 Zimpl 里面，就是下面这样。"#"后面的是注释。

zimpl 复制代码 
var x1 integer >= 0; var x2 integer >= 0; var x3 binary;

maximize income: 3*x1 + 5*x2 + 75*x3 - 0.03*x1^2;
subto material: 2*x1 + 4*x2 <= 100;
subto safety: x1 <= 30;

请读者们自行比较一下这些代码和式 (5) 之间的差别和联系。读者们可以注意到，在这段代码里面根本没有关于怎么求解这个模型的任何一行代码，整段代码里面基本上只有数学公式。

我们写完了这个文件之后，打个比方说，假如我们想用 SCIP 求解器求解这个模型的话，我们可以在 SCIP 求解器里面读取这个模型文件，然后运行求解命令。而如果是不支持 Zimpl 语言的求解器，比如 Gurobi，则可以通过 Zimpl 的转换功能，先转换为 LP 格式，再由求解器读取并求解。

求解方法与求解器

运筹学优化模型的求解算法

关于求解算法的这部分内容，我只能给读者们粗略讲讲原理，因为模型的求解算法这块内容数学原理挺深奥的，而且我自己的数学也不是太好，这块内容没法深入去讲，更何况我最开始就讲了求解算法不是我们这篇文章的重点。所以我这里说个大概的意思，让读者们有个概念。

像我们平时在课上学的那些模型都是有现行的可以求解的算法的，但是在我们实际生活中，接触的这些模型形式，其目标函数和约束都是根据实际问题的情形决定的，如果为每个具体的问题每个模型都去设计一种专门的求解算法，一方面是因为模型的特殊性设计不出来，另一方面数学家就要在被累死之前集体撂挑子不干了。因此，我们一般会使用针对各种模型形式 (非线性规划、混合 0-1 整数规划，etc.) 均适用的通用求解算法来求解这类的模型。

这类通用求解算法大体上可以分为两类：一是以分支定界法 、 割平面法 、 单纯形法 、 还有各种图论算法为代表的"现代穷举法"------精确式算法 ，还有一类则是以 A* 算法、遗传算法、深度 / 广度优先搜索算法、蚁群算法、模拟退火算法为代表的"现代乱猜法"------也就是各类启发式算法和元启发式算法[[3]](#启发式算法和元启发式算法[3])。

在这两种算法当中，前者精确式算法有许多的好处，比如，从理论上说，通过数次迭代之后，精确式算法可以取得模型的全局最优解。但是实际上，精确式算法在处理比较复杂的模型或者大规模算例的时候，可能会出现迭代不收敛导致模型求解不成功，或者求解时间严重过长的情况 ("过长"的意思是说你拿世界上最快的电脑跑到你老死你都跑不出来)。而且有的时候精确是算法还会挑模型，有一些太复杂的非线性模型形式是不接受的。在这种情况下，我们就会诉诸于启发式算法或者元启发式算法去求解。

与精确式算法不一样，启发式和元启发式算法并不追求获得全局最优解，而是想方设法获得一个"能接受"且"足够好"的解。正常情况下，这个解一般都不是问题的全局最优解，但是考虑到启发式算法所具有的灵活性和适应性的优势，能够根据具体问题的特征进行调整和优化，且通常具有较低的时间复杂度和空间复杂度，因此适合处理大规模数据集和复杂的非线性、离散解空间的优化问题。

求解器是怎么工作的

大多数商业求解器都是闭源的计算机程序，其背后被数学专家和工程师精心设计出来的复杂的算法逻辑通常都进行了加密，我们在使用的过程当中是看不到的。而就算是拿开源求解器来说，一个功能完善的求解器，其复杂程度大致与操作系统相当。

!note

我说很复杂，读者们可能没概念，这么说吧：以开源的 SCIP 求解器为例，整个项目包含大约 130 万行代码，其中 C 语言有 94,3647 行，C++ 有 31,3057 行，大大小小的编程语言加起来差不多有十余种[[4]](#[4])，把这东西的工作原理讲清楚的难度不亚于将 Linux 从头实现一遍。你要是想在这篇文章里看到求解器工作原理的深入讲解，怕是太高看我了。

那么，这么复杂的求解器，跑的究竟是精确式算法还是启发式算法呢？实际上，这取决于你使用的具体是什么求解器。对于大多数现代求解器来说，其实是两种算法都有。启发式算法和精确式算法并不是完全独立、不可兼容的，在很多条件下，两者可以交替使用。比如对于一个非线性规划问题，先使用精确式算法求解其线性子问题的精确解，再将这个精确解作为启发式算法的初始解开始迭代搜索；或者，使用启发式算法为精确式算法寻找一个初始可行解，也可以大大降低迭代计算所需的时间。

本章小结

总结一下本章节的内容：在本章节中，我们首先向读者叙述了课堂上学的运筹优化到底有什么问题、为什么无法在实际问题中应用，以及为什么工科生不需要关注典型问题的典型求解算法的具体运算过程。

其次，本章解释了为什么在规划建模领域会产生模型设计和模型求解的分工，从而引出了模型描述语言的概念。最后，还向读者们简单介绍了一下模型的通用求解算法，以及求解器的概念。下一章我们会带着读者手把手地去做运筹优化模型和求解。

手把手带你做运筹优化

事前准备

哥啊我求你先把求解器装上

如果读者们确信是要学运筹优化，还请读者们先把求解器软件和规划建模语言所需的工具都装上。运筹优化这个东西就好比编程，你不实际操作光学了理论是一点用也没有。

本文主要是基于 SCIP 求解器的，下文的例子也都会基于 SCIP Optimization Suite 去讲解，最后会涉及一点 Pyomo，这可能需要 Python。市面上的求解器很多，如果你不确定什么求解器适合自己，那我建议你就安装这个。我先跟还没有了解过的读者们介绍一下 SCIP Optimization Suite。SCIP Optimization Suite 是基于 SCIP 求解器构建的一个运筹优化工具集，是完全开源免费、无需破解的。除了我们下文要用到的混合规划与非线性求解器 SCIP 之外，它还集成了轻量化的规划建模语言 Zimpl。这也就是说读者们在安装好 SCIP Optimization Suite 工具集之后，无需安装额外的规划建模语言工具即可直接使用 Zimpl。除此之外，SCIP 还继承了线性规划求解器单纯形法 SoPlex、通用并行计算框架 UG 和混合整数规划分解求解器 GCG。

工具集可以直接在官网 (https://scipopt.org) 找到文件下载下载。我猜本文的读者大部分使用的应该都是 Windows 操作系统，那你们就需要下载以 -win64.exe 结尾的安装程序文件。安装的流程就是一般软件的安装流程，如果不会的话可以直接在网上搜索"SCIP 求解器安装教程"，或者在 Bilibili 上面也有安装教程的视频[[5]](#[5])。唯一要注意的是如果安装过程中出了问题，可能需要手动配置一下环境变量。这个网上也有教程，我就不赘述了。

尝试进入 SCIP 求解器的命令行交互

安装好 SCIP 求解器之后，读者们可以打开自己计算机的开始菜单，会看见"所有程序"界面下多出了 SCIPOptSuite 这个文件夹，以及"SCIP"和"SoPlex"这两个程序。SCIP 是控制台应用，这意味着我们在 SCIP 中的所有操作都需要 (1) 通过敲命令来实现 (2) 通过其他语言程序交互进行调用实现。我们可以点击 SCIP 程序的图标，或者打开电脑的命令行窗口 (CMD 或 Windows Powershell 都可以)，然后输入 scip，你会看到如下图所示的提示信息，这就说明你已经成功进入了 SCIP 求解器的命令行交互模式。

!note

如果你在这一步失败了，没能进入 SCIP 求解器的交互界面，有多种可能性，你需要根据 CMD 输出的报错提示信息，分析你遇到的问题。最常出现的情况是 CMD 找不到"SCIP"这个程序，这就说明安装器出于某种原因没能被正确配置你的计算机环境变量。在这种情况下，你需要手动进行配置。这很简单，网上到处都是解释什么是环境变量以及如何配置环境变量的教程，我这里就不赘述了。

log 复制代码 
SCIP version 9.2.0 [precision: 8 byte] [memory: block] [mode: optimized] [LP solver: Soplex 7.1.2] [GitHash: 74cea9222e]
Copyright (c) 2002-2024 Zuse Institute Berlin (ZIB)

External libraries:
  Soplex 7.1.2         Linear Programming Solver developed at Zuse Institute Berlin (soplex.zib.de) [GitHash: b040369c]
  CppAD 20180000.0     Algorithmic Differentiation of C++ algorithms developed by B. Bell (github.com/coin-or/CppAD)
  TinyCThread 1.2      small portable implementation of the C11 threads API (tinycthread.github.io)
  MPIR 3.0.0           Multiple Precision Integers and Rationals Library developed by W. Hart (mpir.org)
  ZIMPL 3.6.2          Zuse Institute Mathematical Programming Language developed by T. Koch (zimpl.zib.de)
  AMPL/MP 690e9e7      AMPL .nl file reader library (github.com/ampl/mp)
  PaPILO 2.4.0         parallel presolve for integer and linear optimization (github.com/scipopt/papilo) (built with TBB) [GitHash: 2d9fe29f]
  Nauty 2.8.8          Computing Graph Automorphism Groups by Brendan D. McKay (users.cecs.anu.edu.au/~bdm/nauty)
  sassy 1.1            Symmetry preprocessor by Markus Anders (github.com/markusa4/sassy)
  Ipopt 3.14.16        Interior Point Optimizer developed by A. Waechter et.al. (github.com/coin-or/Ipopt)

reading user parameter file <scip.set>

SCIP>

从这些信息中，读者们可以看出笔者现在使用的 SCIP 版本为 9.2.0。详细叙述了 SCIPOptSuite 组件所包含的各个模块，其开发者、贡献者，也可以看到 SCIP 求解器的版权属于德国的 ZIB 研究所。

接下来，我们现在先不急着进行下一步操作，而是先输入 quit 命令退出去。这是因为读者们现在还没有一个能求解的模型，我们首先要用 SCIP 自带的 Zimpl 先写一个模型。

编写 Zimpl 模型

尽管读者们大可把滚动条滚到文章上面去，直接复制笔者写好的那个 Zimpl 模型来求解，但是笔者还是希望读者们能够去简单了解一下 Zimpl 这种语言及其语法。

Zimpl 是由德国 ZIB 研究所开发的一种轻量化的特定领域语言 (little language)，用于将问题的数学模型描述转译为线性或 (混合) 整数规划程序，并保存为 (希望是) 能被线性规划或混合整数规划的求解器求解的 lp 或 mps 文件格式。尽管手册里说 Zimpl 主要是面向线性规划 (LP) 和混合整数规划 (MIP) 的，但实际上经过本文笔者测试，Zimpl 完全可以用于编写非线性问题的，无非是求解器接不接受的问题。

Zimpl 并没有一个专用的编辑器，不过，由于 Zimpl 的代码就是纯文本，所以任何文本文件编辑器甚至是电脑记事本都可以用来编写 Zimpl。不过笔者还是会建议你去找一个支持 Zimpl 语言、带有高亮功能的代码 IDE，例如，你可以在 Visual Studio Code 中使用 VSZimpl 插件，或者在 Vim 里安装 1995parham/vim-zimpl。

!note

不至于吧，这篇文章的读者里真的有人连文本文件是什么都不知道吗？呃......从当代大学生的一般素质来看还真有可能。这个问题你要是不知道的话自己去查一下好吧，简单的来讲，文本文件就是只包含文字和符号的电脑文件，可以用任何文本软件都可以打开编辑，比如电脑记事本。

关于 Zimpl 的语法，笔者近期在翻译 Zimpl 语言的用户手册，项目名为 zimpl-doc.zh_CN，在 Github 和 Gitee 平台上同步更新，目前已经翻译到第四章了。读者可以直接前往链接地址访问和下载 PDF 文件。(当然，笔者也十分欢迎任何人加入到当前的翻译工作中来。)

求解你的第一个规划模型

保存模型定义文件

Zimpl 代码文件的后缀名是 .zpl，这也就是说，我们可以把我们刚才写好的那个文件保存为 steel_factory.zpl，然后保存在计算机文件目录的任何一个位置。紧接着，我们在我们保存文件的位置打开计算机的命令行。

!note

为了防止本文的读者们不知道，详细来说：一般情况下，在 Windows 系统上你可以按住键盘上的 Shift 按键，然后右键点击保存 steel_factory.zpl 的那个文件夹的任意空白位置，然后选择"在此处打开powershell窗口(s)"。而如果你使用的是 Windows 11，这个操作还要更简单一些------直接在文件夹空白位置右键即可找到"在终端中打开(T)"选项。Mac 的操作我不了解，因为没用过。Linux 用户则不需要我教。

进入求解器的命令行交互

弹出终端窗口之后，我们像前文那样，首先输入 scip 命令进入 SCIP 求解器的命令行交互界面。在这种情况下，如果我们要对模型进行求解，我们需要首先将模型读取到求解器内。因此，我们首先需要使用读取命令 read：

复制代码 
read steel_factory.zpl

!note

其实 SCIP 求解器也支持直接使用 -f 参数指定模型文件求解，完整的命令形式是

bash 复制代码 
scip -f steel_factory.zpl

直接在终端里执行这个命令就可以立即求解模型。但是因为我们后面还要讲解怎么查看求解后各个变量的值，所以我们不直接使用这个命令，而是选择进入 SCIP 的交互模式，然后用 SCIP 的内部命令操作。

在这种情况下，由于求解器命令行的运行目录和文件的保存目录在同一级目录 (文件夹) 下，求解器能够识别并找到这个名为 steel_factory.zpl 的 Zimpl 脚本文件。否则的话，求解器就会提示找不到文件。在这种情况下，就可能要用到相对路径或者绝对路径来指引文件的正确位置，至于相对路径和绝对路径怎么写的问题，请读者们自己上网查询，本文中不会详细解释。

如果你的文件目录指定是正确的话，那么接下来你应该会看到求解器弹出了如下的提示信息。

log 复制代码 
read problem <steel_factory.zpl>
============


base directory for ZIMPL parsing: <C:\Users\asus\Desktop>

original problem has 4 variables (1 bin, 2 int, 0 impl, 1 cont) and 3 constraints

从提示信息中可以看出：我们的这个模型包含 1 个 0-1 变量 (bin)，2 个整型变量 (int)，还有一个特殊的连续变量 (cont)。这是因为我们定义的这个模型是一个非线性模型，SCIP 会通过引入额外的连续变量实现对非线性约束的处理。这个读者们可以暂时不必关心。

运行求解

在这种情况下，我们直接输入 optimize 命令，求解器就会开始求解模型了。

查看模型的求解结果

查看目标函数值

如果读者们上述的操作都是正确的，那么接下来应该会看见下图所示的界面。这说明 SCIP 求解器已经正确求解了模型。

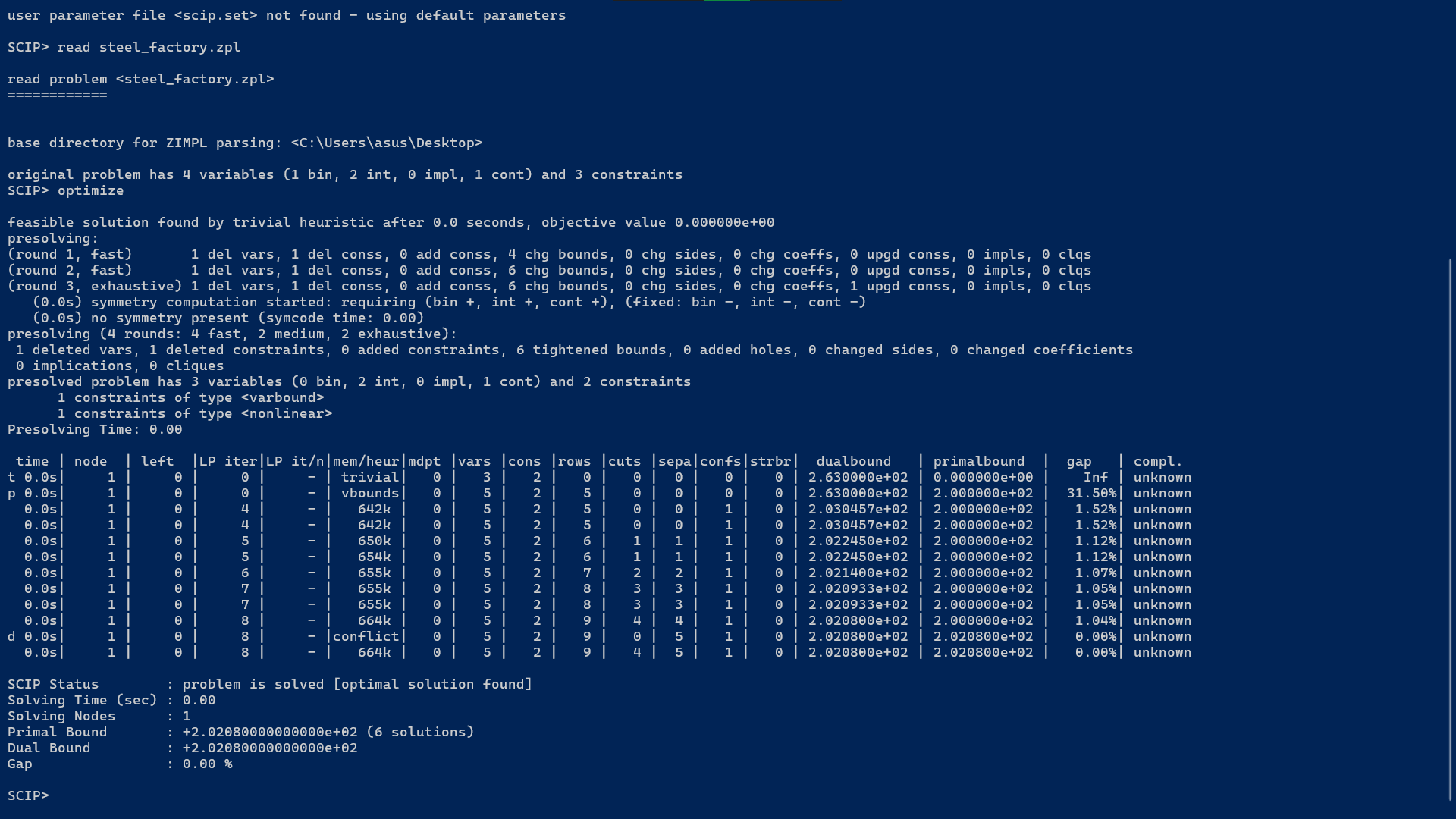
其中，此处最后的六行信息就是模型最主要的求解结果。其中，Primal Bound 即模型的原始边界，也就是模型的最优可行解所对应的最优目标函数的取值。在本文所述的这个钢铁厂问题的模型当中，这也就是在说，按照求解器给出的生产方案，钢铁厂最终的收入是 202.08 万块钱。

查看目标函数值

我们使用 display solution 命令，可以让求解器输出最终给出的生产方案。读者们可以看到，这里给出的最优生产方案是生产 1 份 x3 产品、8 份 x1 产品和 25 份 x2 产品。

log 复制代码 
SCIP> display solution

objective value:                               202.08
x3                                                  1   (obj:0)
x2                                                 21   (obj:0)
x1                                                  8   (obj:0)
objvar                                         202.08   (obj:1)

在求解器输出的信息当中，最后六行信息的具体含义如下表所示。

字段名 输出值 含义说明
SCIP Status problem is solved [optimal solution found] 问题已被成功求解，并找到了一个最优解。这是最理想的状态。
Solving Time (sec) 0.00 求解耗时（单位：秒）。这里表示 SCIP 非常快地在 0.00 秒内就完成了求解。
Solving Nodes 1 Branch-and-Bound 搜索树中探索的节点数。这里仅用了一个节点，说明问题较小或者初始启发式解就非常接近最优。
Primal Bound +2.02080000000000e+02 (5 solutions) 当前找到的最优可行解的目标函数值（即最小化/最大化的值）。括号里说明总共找到过 5 个可行解。
Dual Bound +2.02080000000000e+02 松弛后的理论最优下界（或上界）。当 primal 和 dual 相等时，就说明最优解已经被找到。
Gap 0.00 % 表示当前解和理论最优值之间的相对误差百分比。Gap 为 0%，说明已经找到了全局最优解，且无须继续搜索。

: SCIP 求解器结果的解读

不是啥玩意儿就对偶边界来的

这里关于对偶问题、对偶边界还有相对间隙的问题我们可以好好说道说道。

在使用通用求解器 (比如 Gurobi、CPLEX、BARON 等) 求解数学规划模型时，我们常常会在求解日志中看到一个叫 Gap 的指标，它反映了当前求解进度与全局最优之间的"距离"。这个 Gap 的含义其实是：当前找到的最优可行解（也叫 Primal Bound）和理论上最好的下界（也叫 Dual Bound 或 Relaxation Bound）之间的相对差距^[[6]](#当前找到的最优可行解（也叫 Primal Bound）和理论上最好的下界（也叫 Dual Bound 或 Relaxation Bound）之间的相对差距[6])^。

Gap 越小，说明我们找到的解越"接近"最优解。很多求解器会在 Gap 小于某个阈值（比如 0.1%）时自动终止，认为"够用了"。

通俗来讲，这就好比你去考试，考试之前老师先让全国考试状元把这个卷子做一遍，比如这个时候你看到状元的考试分数是 133 分，你就知道你的考试分数越接近 133 分，你的成绩就越好。

!definition\] 相对间隙 相对间隙定义为如下式 (6) 所示的形式。 \\\[G_r = \\frac{\|p\^\* - d\^\*\|}{\\max(\|p\^\*\|, \|d\^\*\|, 1)}\\tag{6} \\

其中，\(G_r\) 代表相对间隙的值 (百分比)，\(p^*\) 是指当前求解结果中的最优解对应的目标函数的值，也就是我们刚才说的 Primal Bound，而 \(d^*\) 则是对偶边界，也就是前文提到的 Dual Bound。

在这种情况下，就涉及到一个对偶边界和最优上界之间是什么关系的问题。不同类型的模型在估计 Gap 时的方式是不同的。在一些情况下并不能取得 Gap = 0 的结果。

!remark

这个地方多少有点深奥了，我是硬着头皮查阅了一些资料，但是看得也不是很明白。如果我的理解没有问题的话，应该就是像我下面写的这样。但是我也不能肯定我说的一定就对，毕竟求解器的工作原理还是太深奥了。所以下面的这段内容看不懂的读者们可以直接跳过不用看，看懂的读者们记得告诉我一声我到底写得对不对，如果写得不对请务必告诉我这个地方得逻辑到底是什么样的。

我们在运筹学的课内学过，由于线性规划 (LP) 模型具有强对偶性，因此其求解结果中的目标函数的值一定等同于其对偶问题的目标值，也就是

\[p_{\text{LP}}^* = d_{\text{LP}}^*\tag{7} \]

所以只要将当前可行解在原问题和对偶问题中分别取得的最优目标函数值作为 \(p^*\) 和 \(d^*\) 代入上式 (6) 进行计算即可。在一般的 LP 求解算法当中，原问题和对偶问题通常是同时求解的，所以 \(d^*\) 和 \(p^*\) 会被同步更新、实时比较。

但是，对于混合整数规划 (MILP)、非线性规划 (NLP) 或混合整数非线性规划 (MINLP) 中的情况则比较复杂。具体来说，在 MILP、NLP 和 MINLP 中，由于整数与非线性约束的存在，不再拥有 LP 那样的强对偶性。对于一般的极小化目标函数的情形来说，有

\[d^*_{\text{relax}} \le p^*\tag{8} \]

再加上由于这些复杂的模型形式的对偶问题本身也比较难推导、推导出来之后也几乎和原问题一样难以求解，要同时求解原问题和对偶模型也不现实。所以也就不能直接取当前迭代结果下的原问题和对偶问题的目标函数代入式 (6) 来计算对偶边界。在这种情况下：

  1. 对于混合整数线性规划 (MILP)：求解器的做法是：先忽略整数约束，求一个"放松后的 LP 解"（得到下界 Dual Bound），然后再通过分支定界（Branch-and-Bound）等手段慢慢找出可行的整数解（得到上界 Primal Bound）。于是，Gap 就是这两个值之间的差距。由于整数解是离散的，有时候 Gap 很难精确收敛到 0，但求解器会尽可能把它缩小。
  2. 如果是一个凸的 NLP 模型：也就是说目标函数和约束都是凸函数，那情况就和 LP 很像了。现代的 NLP 求解器（比如 IPOPT）也会采用"原始------对偶"方法求解，它们会迭代同时优化变量和拉格朗日乘子，最终让目标函数的 Primal 和 Dual 值一致，因此 Gap 也是能收敛到 0 的。
  3. 对于最复杂的非凸 NLP ，或者 MINLP------既有整数变量，又有非线性结构 ：如果模型是非凸的（比如存在乘积、对数、sin/cos 等非凸函数），那就更麻烦了。求解器通常的做法是：构造一系列凸放松模型（比如通过线性化、包络线、多项式近似等），从中估计出一个可靠的下界 \(d^*_{\text{relax}}\)，然后用启发式算法、局部搜索等去尝试找到一个可行整数解。Gap 就是这两者之间的相对差异。也就是说，对于非凸 NLP 和 MINLP，虽然这里的 \(d^*\) 在求解器日志里面仍然写作 Dual Bound [[7]](#[7])， 尽管其来由实际上与对偶问题并无关联。并且由于没有强对偶性作保障，Gap 不一定能收敛到 0。只有当求解器跑完整个搜索空间，或者用了全局优化方法并证明了没有更优解时，才能确信它是全局最优的。所以，如果你在 MINLP 的求解日志里看到一个 "Gap = 5%"，那并不一定是因为求解器不努力，而是问题本身太难了。

关于求解器的日志怎么读

除了给出的最终结果之外，上图中求解器还输出了很多其他的信息。这些信息涉及到求解器的工作流程，具体来说，在我们上门求解这个非线性混合 0-1 整数规划模型的过程当中，求解器干了这样的三件事儿：

  1. 启发式初解 (feasible solution found by trivial heuristic)
  2. 预处理 / 预求解 (presolving)
  3. 节点处理 / 分支定界主过程 (search process)，记录迭代日志，每一行记录一次状态。

下文我们具体向读者解释一下这三个求解器的工作阶段。

!remark

其实大家完全不用理解这四个阶段分别是在做什么，因为这涉及到求解器的内部机制，涉及大量复杂的算法工程理论，非常的复杂，也不是我们这篇文章要关注的要点，日后也可能不是读者们关注的要点。在这里写这段内容，只是为了让读者们过目，对于求解器的内部工作机制，有一个大概的印象，然后写论文的时候也能方便解释，这样就可以了。

首先，我们聚焦于第一句话："feasible solution found by trivial heuristic after 0.0 seconds, objective value 0.000000e+00"。

这是说，在模型求解的最初阶段，求解器 SCIP 自动尝试使用简单启发式 (trivial heuristic) 找到一个初始可行解。在我们的这个模型里，初始可行解对应的目标值是 0。这是后续分支定界算法开始前的一个好起点，可以加快分支定界算法的求解速度。

紧接着，SCIP 输出了如下的信息。这是 SCIP 求解器的预处理，或者称为预求解 (presolving) 流程。

log 复制代码 
(round 1, fast) ...
(round 2, fast) ...
...
presolving (4 rounds: 4 fast, 2 medium, 2 exhaustive):
 1 deleted vars, 1 deleted constraints, ...

SCIP 求解器在模型求解之前会执行多轮预处理，尝试简化模型。这些操作可以大大减小模型规模，提高求解效率。打个比方说，在一些运筹优化模型当中，有一些变量之间存在函数关系。如果存在函数关系的话，那么一个变量就可以用另一个变量的算式表达来解释。在这种情况下，就能直接删掉其中一个变量来节约迭代求解过程中的内存。如果模型的规模更大，那么，通过这种方式，迭代求解的速度也就会越快。

  • del vars/conss：删除了不必要的变量 / 约束
  • chg bounds：收紧了变量的上下界 (bound tightening)
  • upgd conss：约束被识别为可以加强或替换为更强的形式 (如线性化)

接下来，SCIP 求解器会对模型进行对称检测 (Symmetry computation)。SCIP 检测模型是否存在变量 / 约束层面的对称性。有对称性时，可以通过剪枝减少冗余节点，但这次模型中未发现对称性。

log 复制代码 
symmetry computation started ...
no symmetry present ...

模型经过预处理后，变量数减少为 3 (2 个整数变量 + 1 个连续变量)。而约束数量也减少到了 2 个，其中一个是变量界约束 (在 Zimpl 中变量界约束是在定义变量的时候直接规定了的，并不会用 subto 语句写出来)，另一个则是一个非线性约束。

log 复制代码 
presolved problem has 3 variables (0 bin, 2 int, 0 impl, 1 cont) and 2 constraints
      1 constraints of type <varbound>
      1 constraints of type <nonlinear>
Presolving Time: 0.00

!remark

读者们大可不必关心化简后的模型具体是什么形式，因为模型的化简过程只会考虑求解的难易程度，不会考虑模型与原问题的关联性，所以可读性几乎是可以想象的差。

读者们可以看到，在求解器的迭代日志里面有一张大表，大表具有很多列。这个就是求解器分支定界的主循环的迭代信息了，也是我们首要关注的内容。

列名 含义
time 当前总耗时（秒）
node 当前处理的节点编号
left 剩余节点数（未处理）
LP iter 当前迭代中 LP 求解的次数
dualbound 当前的下界
primalbound 当前的上界（最好的可行解）
gap 相对间隙
compl. 估算的的近似完成度，可以在配置里选用不同的估计算法

: 迭代表中的参数列的含义

一般情况下，在迭代过程中，我们会看着 gap 的值慢慢变小乃至逼近 0，compl. 的值慢慢变大逼近 100%，这个时候就代表我们的模型求解好了。当然，如果你的模型足够复杂的话，也可能出现连续好几个小时 compl. 都不发生变化的情况。这个时候也没有什么好的方法，要么继续等，赌它在宇宙毁灭之前能不能给你输出一个结果来；要么就去换用启发式算法。关于启发式算法怎么搞的问题，就要涉及到很具体的实现了。这个我们放在下回再讲。

本章小结

在本章中，我们手把手地从 SCIP Optimization Suite 的安装开始，带领读者一步一步地求解了一个形式简单的非线性混合整数规划问题的模型 (就是我们在第二章提出的那个钢铁厂的问题的模型)。其中，我们用读者大概率看不懂的语言详细分析了求解器迭代过程中针对相对间隙的定义和计算的问题，在此之后还向读者解释了求解器输出的日志中的各种内容的具体含义。

其他优化建模工具

在本节中，笔者将会向读者们介绍几种常见的优化建模语言和优化求解器，以便读者们可以挑选自己喜欢的优化建模工具。

!remark

想来这个章节放在这里其实出得有点早了，因为本文的读者可能还没有用过其中的一种或几种，现在跟读者们提这样或那样的规划建模语言分别有什么优势劣势读者们可能听得一头雾水。我原本想要在这里写的是基于运筹优化方案建模求解 TSP 模型的实战，但是后来发现这部分的内容太长了，所以我打算放到下一期内容里去讲解。借着这个章节我可以给读者们普及一些诸如文件格式之类简单的概念，所以这一章节请读者们先简单过一遍。

建模语言

大体上来看，现在市面上存在的几种常见的规划模型描述语言，大致可以被分为如下的几类：

首先第一类，是以 .lp 和 .mps 为文件后缀名的模型描述文件。这两种文件格式都是比较老的，只能保存线性模型。关于其来历，LP 文件可能和当年的 LP Solve 软件有关 (这个软件现在还能用)，而 MPS 文件的历史更是可以追溯到 1964 年的 IBM System/360[[3:1]](#[3:1]) 时期。这俩老东西或多或少都有点问题，比如 LP 文件不能批量创建约束 (这就意味着，如果你的模型有 100 个约束，即使这些约束形式都差不多，你还是得一条一条写)，而 MPS 文件更是可读性爆差。具体有多差呢？呃......就像下面[[4:1]](#[4:1])这么差。

!remark

MPS 文件基本上不是给人看的，你说它能手写吧，早期的人也就是这么写的，但我觉得把，你要是没啥大病，不建议你瞎折腾着尝试去写。

mps 复制代码 
NAME          shortestpath.lp
ROWS
 N  Obj
 E  c0
 E  c1
 E  c2
COLUMNS
    INTSTART  'MARKER'       'INTORG'
    x0        Obj        17  c0            1
    x0        c2          1
    x1        Obj        47  c1            1
    x1        c2          1
    x2        c1          1  c0           -1
    x2        Obj        19
    x3        Obj        53  c0           -1
    x4        c1         -1  Obj          23
RHS
    RHS       c2          1
BOUNDS
 UP Bound     x0          1
 UP Bound     x1          1
 UP Bound     x2          1
 UP Bound     x3          1
 UP Bound     x4          1
ENDATA

但是 LP 和 MPS 这种文件也有好处，就是其历史悠久，而且形式比较基本，所以各种求解器都会提供相应的文件格式支持，也就是说，大多数的求解器都能读取并且对其运行求解。所以有一些数学规划模型描述语言也会提供软件支持，允许你把你写好的模型另存为 LP 或者 MPS 格式的文件，以便那些没有提供相应语言的支持的求解器能够求解你的模型。

第二类，是以 IBM CPLEX、AMPL 商用级的专业建模语言，通常都是在相应的数学规划求解系统软件里面用的。这些语言的语法是被精心设计过的，尽可能让你在写模型定义的时候用起来方便。一般都很完善，很重量级，有大公司撑腰，而且自带威力强大的求解器，比如 CPLEX 就有专门的集成环境 IBM ILOG CPLEX Optimization Studio。但是这些语言一般都是收费的，而且订阅价格不菲。读者们现在可能正在使用的 LINGO，大致也可被算作是这一类，只不过 LINGO 的设计比较轻量化。

第三类，就是各种求解器的编程语言 API (application program interface，即应用程序接口)，也就是供你在编程语言中调用求解器的工具。比如 Gurobi 用户肯定对 gurobipy 很熟悉，它就是 Gurobi 求解器的 Python API。这类的编程语言 API 通常就是在常见的编程语言 (比如 C++ 或者 Python) 的编写环境 (比如源代码文件或脚本当中) 导入一个求解器提供给你的库。这个库里面定义了一些用于跟求解器互动的基本的函数、方法或类，以供你将你的数学模型表述"实例化"为求解器能够读取的集合、变量、约束、目标函数的形式。

这类 API 的品质可以说跟编程语言挂钩。比如如果你使用的编程语言本身的语法就比较繁琐，那么使用基于这种编程语言构建的 API 在编写模型表述的时候就可能会比较麻烦。而且，使用这类规划建模语言往往还要付出额外的学习成本。虽然编程语言本身可能是你所熟悉的，但是各个求解器定义的 API 形式都不一样。如果你在使用一种以上的求解器，就很容易混淆；另一方面，我们在日常生活中编程的时候通常情况下并不会把所有的 API 都记下来，而是边查边用。但是吧，如果你是在建模的过程中这样做，如果某个求解器的 API 你没用熟练，本来你脑子的大部分内存都被用于思考模型该怎么设计的问题。这个时候如果还要去关注 API 是怎么定义，脑子可能就不够用了。

然而求解器 API 的优势也很明显，那就是你可以直接利用你所使用的编程语言的优势来处理模型的各种参数。打个比方说，假如你要求解围绕一组地理坐标点送外卖的最短路径，你就可以在一个文件里面写 TSP 模型的定义，在另一个文件里面写数据分析代码，从地理数据、道路路网信息中解析出道路长度、车流量、拥挤程度之类的数据，然后在模型的定义文件里面读取一下另一个文件里面计算出来的这些数值直接作为模型的参数输入，运行求解一步到位。而对于模型输出出来的解，你也可以直接用编程语言绘图可视化或者做进一步分析。这对求解一些背景特别复杂的模型来说尤其有用。关于这些技巧，我们会在后文跟读者详细解释的。

建模语言 语法 求解器 模型规模 模型复杂度 模型类型
徒手写 LP 人间折磨 被动兼容 小规模 简单 混合线性
Zimpl 清晰易懂 主动兼容 一般 一般 混合非线性
Pyomo 清晰但复杂 主动兼容 大规模 复杂 混合非线性
求解器 API 取决于语言 一对一 大规模 复杂 取决于求解器
LINGO 傻瓜式 专用 小规模 复杂 混合非线性
商用级语言 清晰易懂 专用 大规模 复杂 混合线性

: 几种不同的规划模型描述语言或其类别的横向比较

我们刚才说到：由于每个求解期都定义了自己的 API，为了使用每一个求解器，单独去学习相应的 API 就会导致学习成本很高。于是有人就想到可以设计跨平台的规划建模语言，提供所有求解器的支持。其中最著名的当属 Pyomo。这是一种基于 Python 构建的规划建模语言，你只要学会了 Pyomo 语法、写好模型。求解的时候，可以通过 Pyomo 去调用其他求解器求解。而 Pyomo 提供了跨平台支持，能够把你定义的模型转化为其他求解器需要的模型实例，这样你就不用把每一个求解器的 API 语法都学一遍了。还有本文上文提到的 Zimpl 大致也属于这一类，但是 Zimpl 比较轻量化，工作原理就是把你写好的 Zimpl 代码转化为 .lp、.zpl 或者对于非线性模型，转化为 AMPL 的 .nl 格式，然后交给支持这些文件格式的求解器求解。

当然还有一些工具，笔者也没用过，所以也就不罗列于此了。

求解器

笔者用过的求解器不算很多，除却 LINGO 本身就是一个求解器之外，我用的主要就是商用的 Gurobi 和非商用的开源求解器 SCIP，以及专门针对连续非线性凸优化求解的 ipopt。

虽然从名义上说 Gurobi 求解线性模型的速度是首屈一指的，但是实际上我在实际使用过程中也感觉不出来它的求解速度和 SCIP 有什么区别。不知道是不是我的模型规模还没有大到一定的程度，我是觉得它俩换来换去，说到底能求解出来的模型总能求解出来，求解不出来的还是求解不出来。除此之外，SCIP 求解器是开源的，而且不需要额外设置就能直接求解非线性混合 0-1 整数模型，而 Gurobi......我不好说，我从来没能正确启用它的非线性求解功能。而且还要申请学术许可证，也是比较麻烦的事情。

最后就是 Ipopt 了。这个没什么好说的，SCIP Optimization Suite 已经整合了 Ipopt，如果你的模型是非线性的又不包含整数变量，直接用它就好了。

还有就是 LINGO。其实我一直怀疑 LINGO 是可以调用外部求解器的，比较它作为一门模型描述语言本身还是很完备的，但是我从来不知道怎么操作。而且 LINGO 界面太老、破解版本也太旧了，很多功能不更新，就会比较折磨人。

本章小结

在本章中，笔者向读者介绍了几种常见的规划建模语言的类别和三种常见的求解器工具，给出了简要的横向对比。

总结

其实我最先预计的这篇博客文章的内容是比现在要长的，但是最后我删掉了部分章节。考虑到如果一次交代太多内容的话，作为入门教程，读者可能招架不过来。所以我决定将一些内容放到下一期博客里面去讲，这期博客也相对更简单一些。主要就是把求解器装上、测试了一个简单的模型求解，然后讲解了一些求解器基本的工作原理。就这样。

虽然本文的标题叫做"一篇文章给你讲清楚运筹优化到底怎么学"，某种意义上本文确实是讲清楚了。但是还不够深入。只能说我也没想到还会有下篇。总之，下一期教程大概会涉及到 TSP 模型建模求解的实践教学。只是不知道什么时候能更新，所以读者们敬请期待。

  1. 极大值函数 \(\max f\) 实际上就是对 \(f\) 取负再求其极小化值 \(\min -f\)，故而在优化问题的形式化表述中不作此区分。 ↩︎

  2. "Programming"在英语里既有"编程"的意思，也有"规划"的意思。在英文文献中，为了以示区分，有的时候会加上一个"Mathematical"的前缀，写作"Mathematical Programming Language"。 ↩︎

  3. 元启发式算法 (Metaheuristic Algorithm)，有时也被称作现代启发式算法 (Modern Heuristic Algorithm)，该名词被首次提出于 1987 年。从广义的概念上来讲，所有元启发式算法本质上也是启发式算法的一种，属于启发式的上层范畴。但它们的侧重点在于"如何设计或组合启发式"。本文中不对启发式算法和元启发式算法的概念作太详细的区分，读者们知道就好。 ↩︎ ↩︎

  4. 通过 VS Code Counter 插件统计代码行数得出的结果。 ↩︎ ↩︎

  5. 001_windows安装SCIP教程，BV1X54y1u7YE，视频有点老了，虽然是 2023 年发布的，但是在演示上用的是 Windows 7 操作系统。不过作为参考肯定是没有问题的。 ↩︎

  6. "下界"是相对于极小化目标函数而言的，极大化目标函数则反之对应上界。 ↩︎

  7. 按照 or.stackexchange 上的网友的提问和回答，貌似在学术论文里面人们也会像这样直接用 Dual Bound 称呼放松后的问题得到的目标值，即使这一目标值与"对偶"的定义无关。网友觉得更合适的名称是 optimality gap ，另请参阅 https://or.stackexchange.com/questions/3200/dual-bounds-of-integer-programming-problems 。 ↩︎

热门推荐
01从零安装 LLaMA-Factory 微调 Qwen 大模型成功及所有的坑02KGG转MP3工具|非KGM文件|解密音频03YOLOv8入门 | 重要性能衡量指标、训练结果评价及分析及影响mAP的因素【发论文关注的指标】04【SpeedAI科研小助手】2分钟极速解决知网维普重复率、AIGC率过高，一键全文降！文件格式不变，公式都保留的！05组基轨迹建模 GBTM的介绍与实现（Stata 或 R）06Coze扣子平台完整体验和实践（附国内和国际版对比）07Ubuntu24.04安装中文输入法08YOLOv5改进 | 添加CA注意力机制 + 增加预测层 + 更换损失函数之GIoU09DeepSeek各版本说明与优缺点分析10yolov8实战第五天——yolov8+ffmpg实时视频流检测并进行实时推流——（推流，保姆教学）