目录
引言
在大数据处理场景中,我们常常面临海量数据的存储和快速查询问题。布隆过滤器(Bloom Filter)作为一种高效的概率型数据结构,能够在节省大量内存空间的同时,快速判断一个元素是否可能存在于集合中。今天,就让我们深入探究布隆过滤器的奥秘。
布隆过滤器的起源与概念
起源

布隆过滤器由Burton Howard Bloom在1970年提出。设想一个新闻客户端推荐系统的场景,服务器记录了用户看过的所有历史记录,当推荐新内容时需要过滤掉已经看过的内容。如果用哈希表存储用户记录,会浪费大量空间;用位图存储,又只能处理整形,无法处理字符串等其他类型。于是,布隆过滤器应运而生,它将哈希与位图结合,有效解决了这类问题。
概念
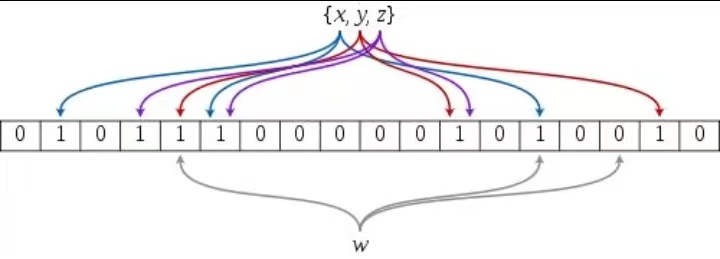
布隆过滤器是一种紧凑型的概率型数据结构。它的核心原理是使用多个哈希函数,将一个数据映射到位图结构中。通过这种方式,它可以高效地插入和查询元素,告诉我们"某样东西一定不存在或者可能存在" 。
布隆过滤器的工作原理
插入操作
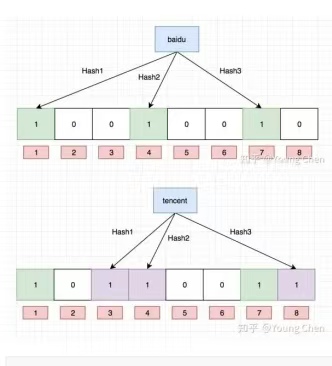
当向布隆过滤器中插入一个元素时,会使用多个哈希函数对该元素进行计算,得到多个哈希值。这些哈希值对应到位图中的不同位置,然后将这些位置的值设置为1。

例如,向布隆过滤器中插入"baidu" ,假设使用3个哈希函数(Hash1、Hash2、Hash3) ,计算得到的哈希值分别对应位图中的某些位置,将这些位置置为1。
查询操作
查询一个元素时,同样使用这几个哈希函数计算哈希值,然后检查位图中对应位置的值。如果有任何一个位置的值为0,那么可以确定该元素一定不存在于布隆过滤器中;如果所有位置的值都为1,则该元素可能存在。
原理示例代码(C++)
cpp
#include <iostream>
#include <bitset>
#include <string>
// BKDR哈希函数
struct BKDRHash {
size_t operator()(const std::string& s) {
size_t value = 0;
for (auto ch : s) {
value *= 31;
value += ch;
}
return value;
}
};
// APHash哈希函数
struct APHash {
size_t operator()(const std::string& s) {
size_t hash = 0;
for (long i = 0; i < s.size(); i++) {
if ((i & 1) == 0) {
hash ^= ((hash << 7) ^ s[i] ^ (hash >> 3));
}
else {
hash ^= (~((hash << 11) ^ s[i] ^ (hash >> 5)));
}
}
return hash;
}
};
// DJBHash哈希函数
struct DJBHash {
size_t operator()(const std::string& s) {
size_t hash = 5381;
for (auto ch : s) {
hash += (hash << 5) + ch;
}
return hash;
}
};
template<size_t N, size_t X = 5, class K = std::string,
class HashFunc1 = BKDRHash, class HashFunc2 = APHash, class HashFunc3 = DJBHash>
class BloomFilter {
public:
void Set(const K& key) {
size_t len = X * N;
size_t index1 = HashFunc1()(key) % len;
size_t index2 = HashFunc2()(key) % len;
size_t index3 = HashFunc3()(key) % len;
_bs.set(index1);
_bs.set(index2);
_bs.set(index3);
}
bool Test(const K& key) {
size_t len = X * N;
size_t index1 = HashFunc1()(key) % len;
if (_bs.test(index1) == false)
return false;
size_t index2 = HashFunc2()(key) % len;
if (_bs.test(index2) == false)
return false;
size_t index3 = HashFunc3()(key) % len;
if (_bs.test(index3) == false)
return false;
return true;
}
private:
std::bitset<X*N> _bs;
};布隆过滤器的优缺点
优点
查询和插入效率高:时间复杂度为O(K)(K为哈希函数的个数,通常较小),与数据量大小无关。
适合硬件并行运算:哈希函数之间相互独立,方便在硬件层面实现并行处理。
节省内存空间:不需要存储元素本身,在对保密要求高的场景优势明显,比如只需要判断用户是否访问过某些资源,而不需要存储用户信息本身。
能表示全集:在数据量极大时,相比其他数据结构,布隆过滤器可以用来表示全集。
支持集合运算:使用同一组散列函数的布隆过滤器可进行交、并、差运算。
缺
存在误判:即假阳性(False Positive),不能准确判断元素是否在集合中。解决方法可以是建立一个白名单,存储可能会误判的数据。
无法获取元素本身:只能判断元素是否可能存在,不能获取元素具体信息。
不支持直接删除:一般情况下不能从布隆过滤器中删除元素,因为删除一个元素可能会影响其他元素。若采用计数方式删除,又可能存在计数回绕问题 。
布隆过滤器的应用场景
网页爬虫的URL去重
在网页爬虫中,需要爬取大量网页。为了避免重复爬取相同的URL,布隆过滤器可以用来快速判断一个URL是否已经被爬取过。将已经爬取过的URL插入布隆过滤器,每次遇到新的URL时进行查询,若不存在则进行爬取,这样可以大大提高爬虫效率,节省存储空间。
数据库中的数据判重
在数据库中,对于一些大规模数据集,如用户注册信息等,需要判断新插入的数据是否已经存在。使用布隆过滤器可以在不占用大量内存的情况下,快速进行初步判断。如果布隆过滤器判断数据可能存在,再进一步到数据库中进行精确查询。
垃圾邮件过滤
邮件服务器可以使用布隆过滤器来判断一封邮件的发件人或邮件内容是否属于已知的垃圾邮件来源。将已知的垃圾邮件相关信息(如发件人邮箱、关键词等)插入布隆过滤器,当收到新邮件时进行查询,快速过滤掉可能的垃圾邮件,减轻后续处理压力。
总结
布隆过滤器凭借其高效的空间利用和快速查询特性,在大数据处理、网络爬虫、数据库管理等众多领域都有着广泛的应用。尽管它存在一些局限性,如误判和不支持直接删除等问题,但通过合理的设计和结合其他数据结构,依然能在实际应用中发挥巨大的作用。希望通过这篇博客,大家能对布隆过滤器有更深入的理解,并在未来的项目中灵活运用。