游戏中常用的平滑曲线函数：高中生也能看懂的代码分析

移动中常用的平滑曲线函数：

在代码控制2D人物一动时候，为了保证人物在停止停止移动时候出现速度瞬变，卡顿问题，常常使用一个平滑函数，来使得速度按照函数的平滑曲线来逼近目标值。

先看代码：

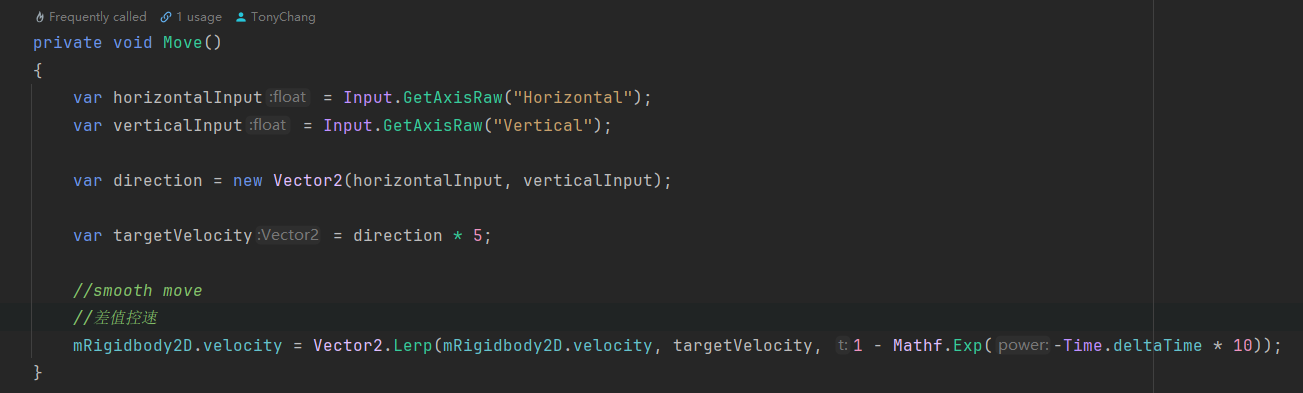
一个在Update中调用的移动函数。

首先通过获取用户输入的坐标方向来确定好人物移动的二维方向（2D游戏）。之后可以设定一个速度数值，赋值给targetVelocity ，作为人物的移动的目标速度。

有了目标速度，我们可以使用插值函数来使人物从当前速度过度到目标速度，从而避免速度突变卡顿现象。

C# 复制代码

	mRigidbody2D.velocity = Vector2.Lerp(mRigidbody2D.velocity, targetVelocity, 1 - Mathf.Exp(-Time.deltaTime * 10));

来看这一行代码：

最外层的插值函数：

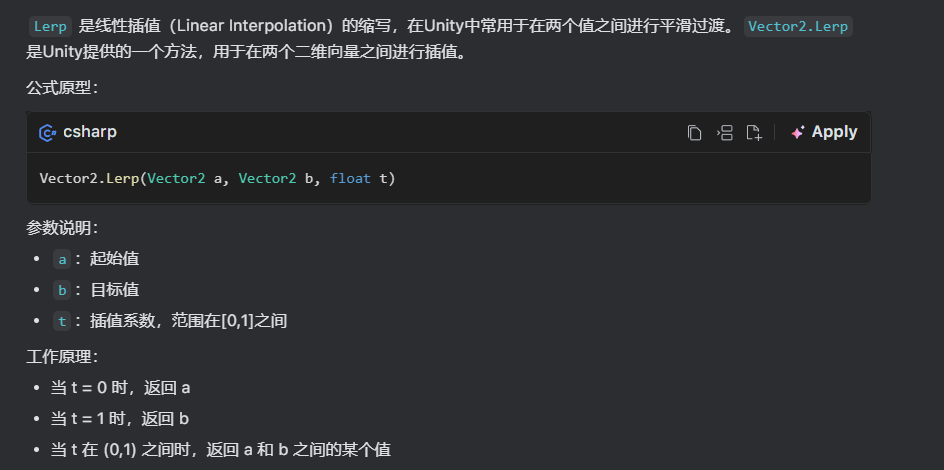
也就是说我们要获取一个中间数值来使得人物从当前速度到目标速度有个过度。

显然我们第三个参数可以填0.5 直接选取中值来作为过度，但是忽略到了移动和帧率的关系，

当帧率高时候，这种固定取中值的方式不免还是有些僵硬。

这里我们抓住帧率这个变量，斟酌一下Lerp的插值系数。

复制代码

1 - Mathf.Exp(-Time.deltaTime * 10)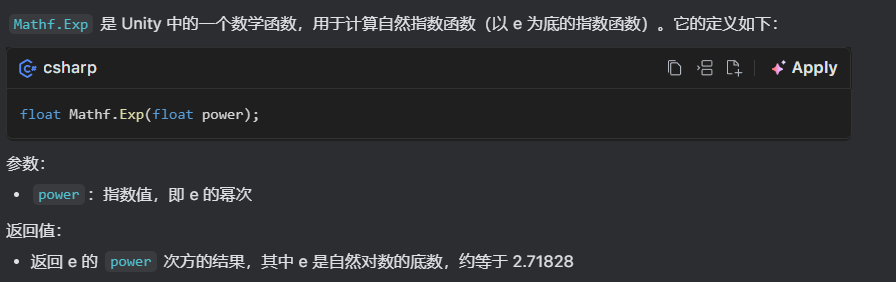

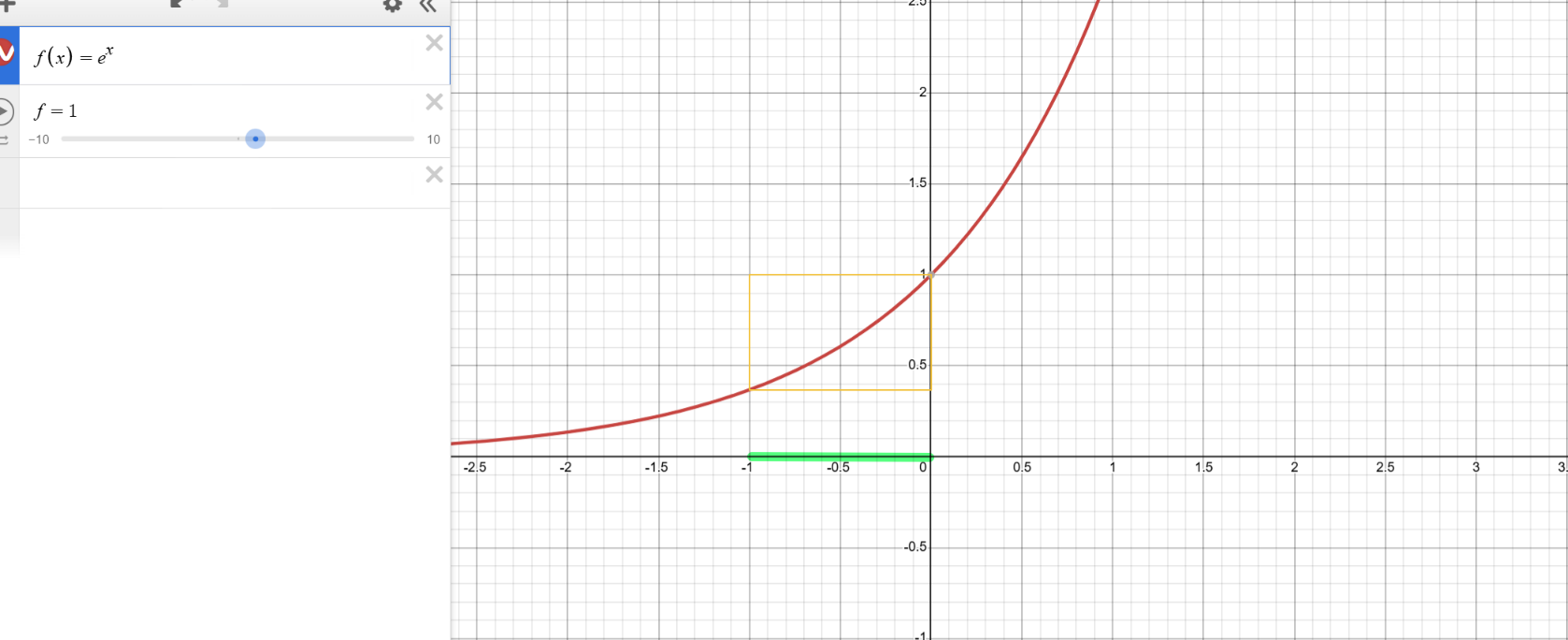
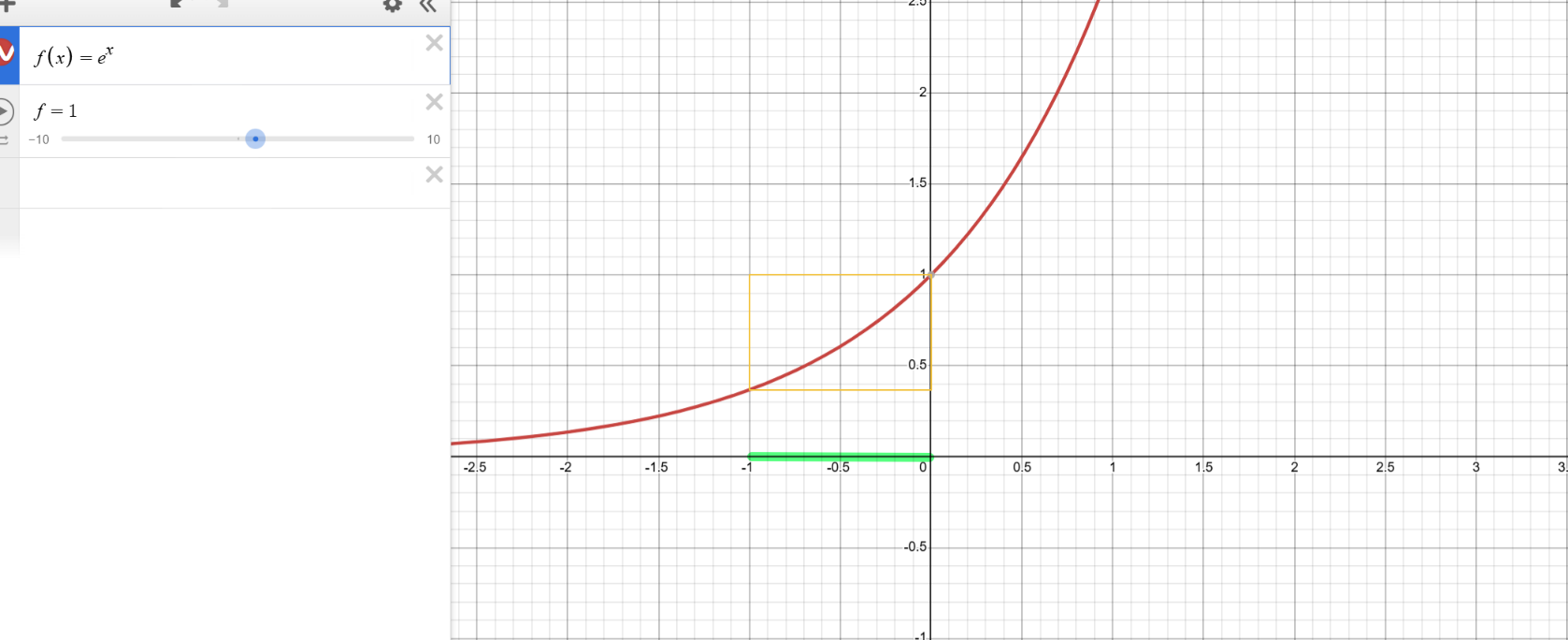
说到"平滑"自然想到高中时候学过的指数函数，没错就是它！选取底数为e的指数函数，如果你用指尖沿着函数曲线滑动，一定会有洗泡泡浴的感觉！什么？没有，发挥一下数学想象哈哈哈哈！

当帧率高时，Time.deltaTime 越小，-Time.deltaTime 越大，越从x轴负向靠近0坐标

取指数函数的数值越接近1 ，也就是插值结果越接近目标值。
当帧率低时，Time.deltaTime越大，-Time.deltaTime 越小，越从x轴负向远离0坐标

取指数函数的数值就越接近0.4 ,差值相对更接近当前状态的数值。

结果更靠近起始值还是目标值，其变化程度是光滑过度的，这样就很好的解决了速度突变的问题。

当然代码中常量数值是可以作为光滑系数来使用的。

总结下：在面对两个数值间突变的情况，我们使用插值函数配合指数函数来做到光滑过度.在游戏开发中常用于实现各种平滑过渡效果，如：角色移动、相机跟随、UI 动画、物理模拟等

由函数曲线和逐行函数分析，使得我们了解到代码背后的数学原理。了解了数学原理，编程过程中也会领略到数学之美，也给游戏开发增点不一样的乐趣。