不同数据场景下的聚类算法

在数据分析和机器学习领域，聚类是一种非常重要的无监督学习方法，它可以帮助我们发现数据中的内在结构，将相似的数据点分组到一起。

本文将介绍几种常见的聚类 算法，包括原型聚类 （如 k-均值、学习向量量化、高斯混合聚类）、密度聚类 （DBSCAN）和层次聚类（AGNES）。

通过浅显易懂的方式介绍它们的原理，探讨它们的适用场景，并通过代码演示如何使用这些算法。

1. 原型聚类：以"中心点"代表群体

1.1. k-均值聚类

k-均值聚类 （K-Means Clustering）是一种非常直观的聚类方法。

它的目标是将数据划分为 k 个簇，每个簇由一个**"中心点"**（质心）代表。

算法的步骤如下：

1. 随机选择 k 个数据点作为初始质心。
2. 将每个数据点分配到最近的质心所在的簇。
3. 重新计算每个簇的质心（即簇内所有点的均值）。
4. 重复上述步骤，直到质心不再变化或达到预设的迭代次数。

k-均值聚类适用于数据分布较为均匀且簇形状较为规则的场景。

例如，对用户群体进行市场细分，或者对图像中的像素进行颜色聚类。

基于scikit-learn的代码示例如下：

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

# 生成模拟数据
X, _ = make_blobs(n_samples=300, centers=4, random_state=42)

# 使用 KMeans 聚类
kmeans = KMeans(n_clusters=4, random_state=42)
kmeans.fit(X)
labels = kmeans.labels_
centroids = kmeans.cluster_centers_

# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')
plt.scatter(centroids[:, 0], centroids[:, 1], s=300, c='red', marker='X')
plt.title("K-Means 聚类")
plt.show()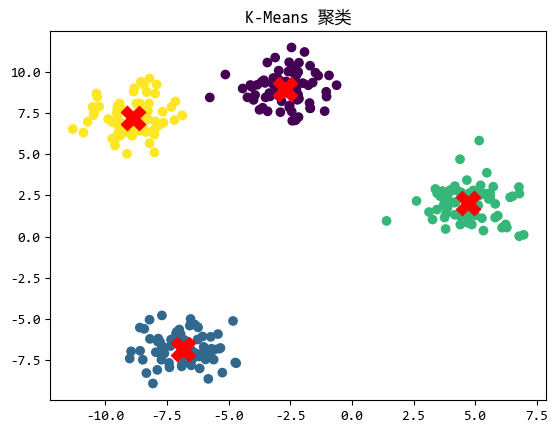

1.2. 学习向量量化

LVQ（Learning Vector Quantization） 是一种受神经网络启发的聚类方法。

它使用一组**"原型向量"**来代表每个簇，算法通过迭代调整这些原型向量的位置，使其更接近属于该簇的数据点，远离其他簇的数据点。

LVQ 的核心思想是通过学习来优化原型向量的位置。

LVQ 适用于数据点分布较为密集且簇边界较为清晰的场景，它在图像识别 和模式分类中表现良好。

虽然scikit-learn没有直接提供 LVQ 的实现，但我们可以使用sklvq库来实现。

安装方式： pip install sklvq

代码示例如下：

from sklvq import GLVQ  # 使用 GLVQ（Generalized Learning Vector Quantization）
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

# 生成模拟数据
X, y = make_blobs(n_samples=300, centers=4, random_state=42)

# 使用 GLVQ 聚类
glvq = GLVQ(random_state=42)
glvq.fit(X, y)

# 获取聚类结果
labels = glvq.predict(X)

# 获取中心点（原型向量）
prototypes = glvq.prototypes_

# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap="viridis")
plt.scatter(
    prototypes[:, 0], prototypes[:, 1], s=300, c="red", marker="X", label="Prototypes"
)
plt.title("广义学习向量量化 (GLVQ)")
plt.show()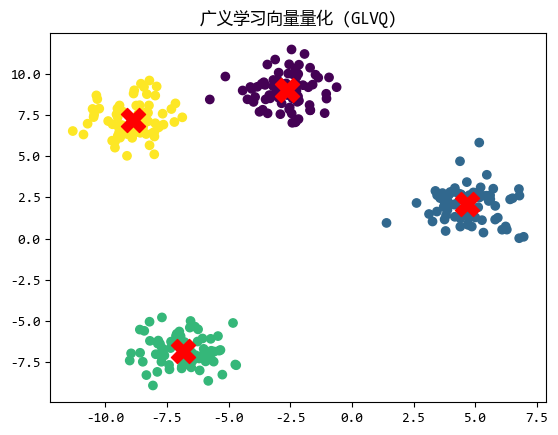

1.3. 高斯混合聚类

高斯混合聚类 （Gaussian Mixture Clustering）假设数据是由多个高斯分布的混合生成的。

每个高斯分布代表一个簇 ，算法通过估计每个高斯分布的参数 （均值 、协方差矩阵 和权重）来确定簇的形状和位置。

高斯混合聚类比** k-均值**更灵活，因为它可以捕捉到簇的形状和大小的变化。

高斯混合聚类适用于簇形状不规则或数据分布较为复杂的情况。

例如，对金融数据中的异常交易进行聚类分析。

代码示例如下：

from sklearn.mixture import GaussianMixture
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

# 生成模拟数据
X, _ = make_blobs(n_samples=300, centers=4, random_state=42)

# 使用高斯混合聚类
gmm = GaussianMixture(n_components=4, random_state=42)
gmm.fit(X)
labels = gmm.predict(X)

# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')
plt.title("高斯混合聚类")
plt.show()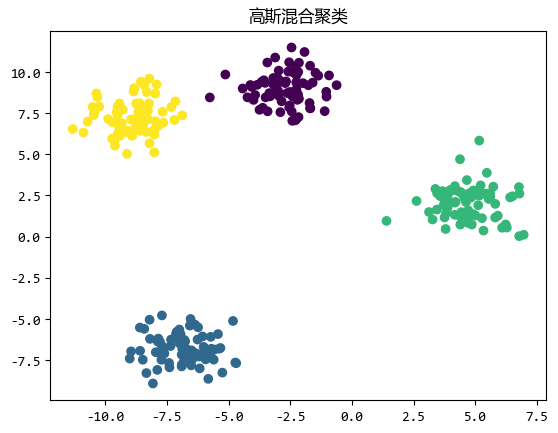

2. 密度聚类：发现任意形状的簇

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的聚类算法。

它的核心思想是：如果一个点的邻域内有足够的点（即密度足够高），那么这些点可以被划分为同一个簇。

DBSCAN 使用两个参数：

• eps：邻域半径，用于定义**"足够近"**的范围。
• min_samples：核心点的邻域内必须包含的最小点数。

DBSCAN的优点是可以发现任意形状的簇，并且能够识别噪声点。

DBSCAN适用于数据分布不均匀、簇形状复杂且存在噪声的场景。

例如，对地理数据中的热点区域进行分析。

代码示例如下：

from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt

# 生成模拟数据
X, _ = make_moons(n_samples=300, noise=0.05, random_state=42)

# 使用 DBSCAN 聚类
dbscan = DBSCAN(eps=0.2, min_samples=5)
labels = dbscan.fit_predict(X)

# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')
plt.title("DBSCAN 聚类")
plt.show()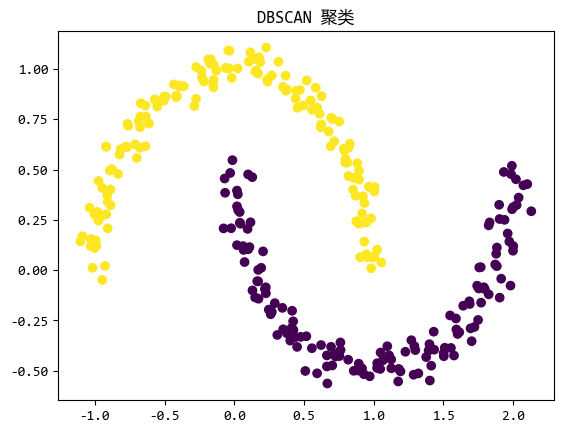

3. 层次聚类：构建数据家族树

AGNES（Agglomerative Nesting）是一种自底向上的层次聚类算法。

它从每个数据点作为一个单独的簇开始，然后逐步合并距离最近的簇，直到达到预设的簇数量或满足其他停止条件。

AGNES 的关键在于如何定义簇之间的距离，常见的方法包括单链接法 、全链接法 和平均链接法。

AGNES 适用于需要逐步分析数据层次结构的场景，例如生物分类学或文档聚类。

代码示例如下：

from sklearn.cluster import AgglomerativeClustering
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

# 生成模拟数据
X, _ = make_blobs(n_samples=300, centers=4, random_state=42)

# 使用 AGNES 聚类
agnes = AgglomerativeClustering(n_clusters=4)
labels = agnes.fit_predict(X)

# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')
plt.title("AGNES 聚类")
plt.show()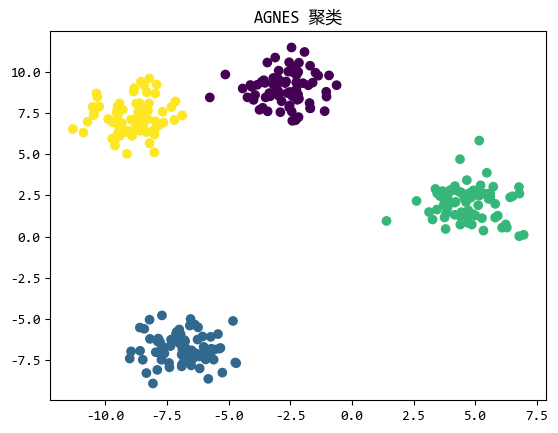

4. 聚类算法对比

常用的几种聚类算法的对比如下：

算法类型	优点	局限性	典型应用场景
K-Means	计算效率高	需预设K值	客户分群、图像压缩
GMM	处理椭圆分布	计算复杂度较高	异常检测、语音识别
DBSCAN	发现任意形状	参数敏感	地理数据、离群点检测
AGNES	可视化层次结构	计算复杂度O(n³)	生物分类、文档聚类

5. 总结

聚类算法的选择取决于数据的特性、问题的需求以及对结果的解释性要求。

k-均值 简单高效，但对簇形状有较强假设；DBSCAN 能够处理复杂形状和噪声；层次聚类则提供了数据的层次结构。

在实际应用中，我们通常需要尝试多种算法，并根据具体问题选择最适合的聚类方法。