Context Cache的使用几乎已经是行业共识,目标是优化大模型首Token的推理延时,在多轮对话,超长System Prompt,超长结构化JSON和Few-shot等应用场景,是不可或缺的。这一章我们主要从原理、一些论文提出的优化项和VLLM开源项目入手,分析下context Cache的实现和适合场景。
重温KV Cache
Context Cache的本质其实是KV Cache在多次请求之间的复用,所以我们先重温下KV Cache的原理。
以下是Transformer的基础模型结构由多层layer串联构成,而KV缓存的是每一层用于Self-Attention计算的历史序列的Key和Value取值,所以缓存向量维度是batch_size * seq_len * num_head * head_dim,(以下可视化来自LLM Visualization和transformer-explainer )
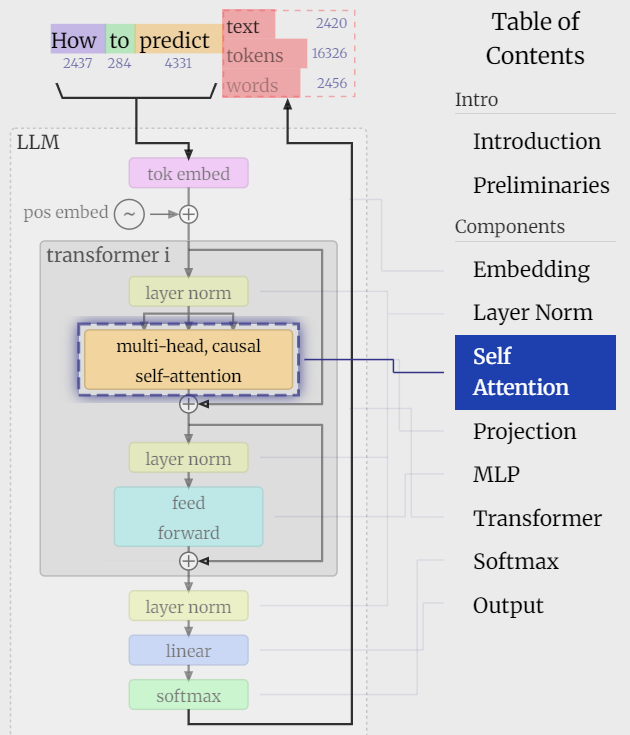
只所以对self-attention的KV进行缓存,因为在Transformer的众多计算单元中只有self-attention是上下文依赖的,也就是在计算第k个token的输出时,需要使用第k个token(Query)和前面K-1个token的(K&V)进行内机计算,使得self-attention的计算复杂度随序列长度平方增长。而如果对历史序列中的KV进行缓存后,每次生成新token只需要计算当前token,这样时间复杂度就可以降为线性(O(n)),显著降低计算量。
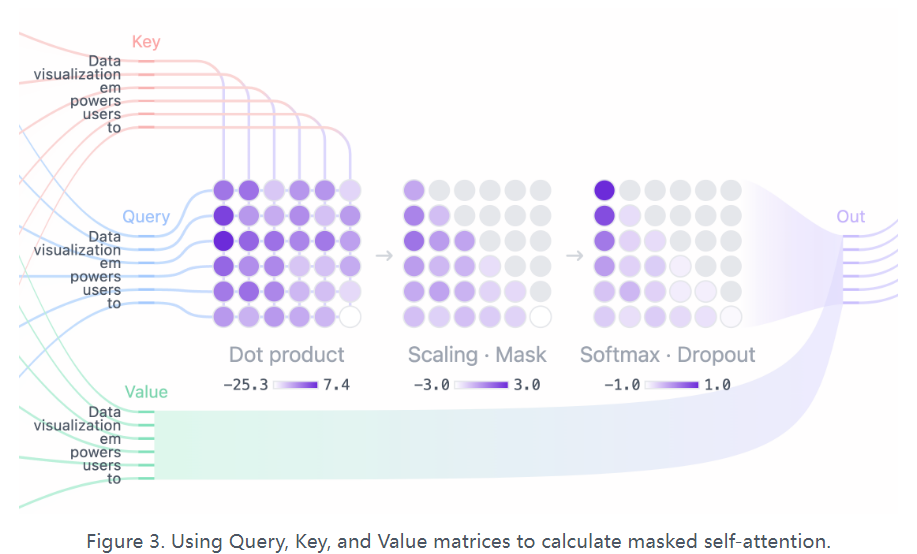
而其他Linear, FFN层的计算都是针对dim层,每个token的计算独立,和历史token无关和序列长度无关,因此也没有缓存的必要。
当然KV Cache也不全是优点,虽然能显著降低推理延时,但是会带来较大的显存占用,占用显存和序列长度、模型层数成正比。
那现在众多大模型API厂商都支持的Context Cache能力和KV cache有哪些区别呢?
首先从cache共享上,因为KV cache只用于单一序列的推理过程中,因此没有任何共享问题,本次推理完成即释放,而context cache会在多次推理请求之间共享,因此对于如何命中Cache,管理Cache, 提升Cache的存储和使用效率,就需要更多的考虑。
其次从使用时机上,KV cache是用于首Token之后的增量预测(auto-regressive Phrase),而Context Cache是用于首Token之前的存量计算(Prompt Phrase)。在context cache出现之前这两个阶段其实有明确的划分,计算prompt的阶段需要对全部序列进行attention计算属于数据计算密集的任务,而解码阶段因为kV Cache的存在更多是存储密集型任务。因此Context Cache是面向首Token延时的优化方案。
KV Cache只是Context Cache的基础使用形式,下面我们会分别就Contxt Cache的几个核心问题包括命中率低,等讨论一些优化方案
并行效率更高: Chunk Attention
- https://github.com/microsoft/chunk-attention/tree/main
- ChunkAttention: Efficient Self-Attention with Prefix-Aware KV Cache and Two-Phase Partition
微软的Chunk Attention通过对KV Cache分段存储,实现self-attention的并发计算,提升长序列self-attention计算效率,经评估自注意力内核的速度可以提高3.2-4.8倍。下面我们结合源码简单说下,源码chunk attention是C语言写的,这里简单转换成python pseudo
- Prefix Aware KV Cache
传统的KV缓存以密集tensor形式存储,大小是batch * head * seq length * dim,当多个序列共享相同的前缀(prompt)时这些kv缓存就是相同的,因此可以进行共享存储,共享存储的大小则是head * chunk length * dim,这里论文选择使用前缀树进行存储。用前缀不用其他存储方式,主要是为了保证位置编码的可用性。这部分就不细说了,就是Trie树,child节点存储的是对应chunk 序列的kv tensor。而这里的分块存储,为后面推理阶段并行self-attention的计算提供了可能性。
\[\begin{align*} \text{Phase 1:} & \forall C_i \in \text{共享块} \\ W_i &= Q_{C_i}K_{C_i}^\top / \sqrt{d} \\ M_i &= \text{rowmax}(W_i) \\ E_i &= \exp(W_i - M_i) \\ N_i &= \text{rowsum}(E_i) \\ O_i &= E_i V_{C_i} \\ \text{Phase 2:} & \forall \text{序列} s \\ M^{\text{total}} &= \text{max}(M_1, M_2, ..., M_k) \\ N^{\text{total}} &= \sum_{i=1}^k \exp(M_i - M^{\text{total}})N_i \\ O^{\text{total}} &= \sum_{i=1}^k \frac{\exp(M_i - M^{\text{total}})O_i}{N^{\text{total}}} \end{align*} \]
- Two-Phase Partition(TPP)
两阶段的推理算法则是如何更高效的使用以上共享前缀的KV Cache。第一步是共享前缀的部分,读取前缀树种存储的chunk KV Cache,进行chunk粒度的并行self-attention计算并存储多个partial attention。
然后剩余未命中前缀的部分,按序列计算剩余attention,之后通过attention合并把把一个序列的多段attention进行合并得到最终的attention.
以下是C转换成python的伪代码
python
# 伪代码体现两阶段推理核心逻辑
class PartialAttention:
def __init__(self, chunk_size=64):
self.chunk_size = chunk_size # 分块大小
self.scale = 1 / sqrt(d_head) # 缩放因子
def chunk_first_phase(self, Q_shared, K_shared, V_shared):
"""
分块优先阶段计算(对应论文Algorithm 1)
Q_shared: [n_shared_seqs, n_heads, d_head]
K_shared: [n_shared_seqs, chunk_size, d_head]
V_shared: [n_shared_seqs, chunk_size, d_head]
"""
# 步骤1: 计算分块注意力得分
attn_scores = torch.einsum('bhd,bsd->bhs', Q_shared, K_shared) * self.scale
# 步骤2: 在线计算局部softmax
max_values = attn_scores.max(dim=-1, keepdim=True).values # [b, h, 1]
exp_scores = torch.exp(attn_scores - max_values) # 数值稳定
# 步骤3: 保存中间结果(对应论文公式1)
partial_attn = {
'exp_scores': exp_scores, # [b, h, s]
'max_values': max_values, # [b, h, 1]
'sum_exp': exp_scores.sum(-1), # [b, h]
'partial_v': torch.einsum('bhs,bsd->bhd', exp_scores, V_shared)
}
return partial_attn
def sequence_first_phase(self, Q_private, partial_results):
"""
序列优先阶段(对应论文Algorithm 2)
Q_private: [1, n_heads, d_head] (单个序列的查询)
"""
# 步骤1: 初始化累计变量
global_max = -float('inf')
global_sum = 0
merged_output = 0
# 步骤2: 合并所有分块结果(对应论文公式2)
for partial in partial_results:
local_max = partial['max_values']
local_exp = partial['exp_scores']
local_sum = partial['sum_exp']
local_v = partial['partial_v']
# 调整指数差值
adjust_factor = torch.exp(local_max - global_max)
# 更新全局统计量
new_global_max = torch.max(global_max, local_max)
new_global_sum = global_sum * adjust_factor + local_sum * torch.exp(local_max - new_global_max)
# 更新输出
merged_output = merged_output * adjust_factor + local_v * torch.exp(local_max - new_global_max)
# 保存新全局值
global_max = new_global_max
global_sum = new_global_sum
# 步骤3: 最终归一化
return merged_output / global_sum.unsqueeze(-1)而之所以attention可以通过局部计算再合并后效果和原始attention一致,不过是因为指数计算的变换,我们抛开论文里面不太好理解的pseudo code,看一个具体的case
- 步骤1:分块计算中间结果
- 块1(s₁, s₂):
- 计算局部最大值:m₁ = max(s₁, s₂)
- 调整后指数:e^{s₁ - m₁}, e^
- 局部分母:sum₁ = e^{s₁ - m₁} + e^
- 块2(s₃, s₄):
- 计算局部最大值:m₂ = max(s₃, s₄)
- 调整后指数:e^{s₃ - m₂}, e^
- 局部分母:sum₂ = e^{s₃ - m₂} + e^
- 步骤2:合并中间结果
- 全局最大值:M = max(m₁, m₂)
- 调整因子:
- 块1调整因子:α = e^
- 块2调整因子:β = e^
- 合并的分母
text
total_sum = α * sum₁ + β * sum₂
= e^{m₁ - M}*(e^{s₁ - m₁} + e^{s₂ - m₁}) + e^{m₂ - M}*(e^{s₃ - m₂} + e^{s₄ - m₂})
= e^{s₁ - M} + e^{s₂ - M} + e^{s₃ - M} + e^{s₄ - M}- 合并后的attention计算结果
text
total_sum = α * sum₁ + β * sum₂
= e^{m₁ - M}*(e^{s₁ - m₁} + e^{s₂ - m₁}) + e^{m₂ - M}*(e^{s₃ - m₂} + e^{s₄ - m₂})
= e^{s₁ - M} + e^{s₂ - M} + e^{s₃ - M} + e^{s₄ - M}空间利用更高:Radix Attention
- SGLang Efficient Execution of Structured Language Model Programs.
- https://github.com/sgl-project/sglang
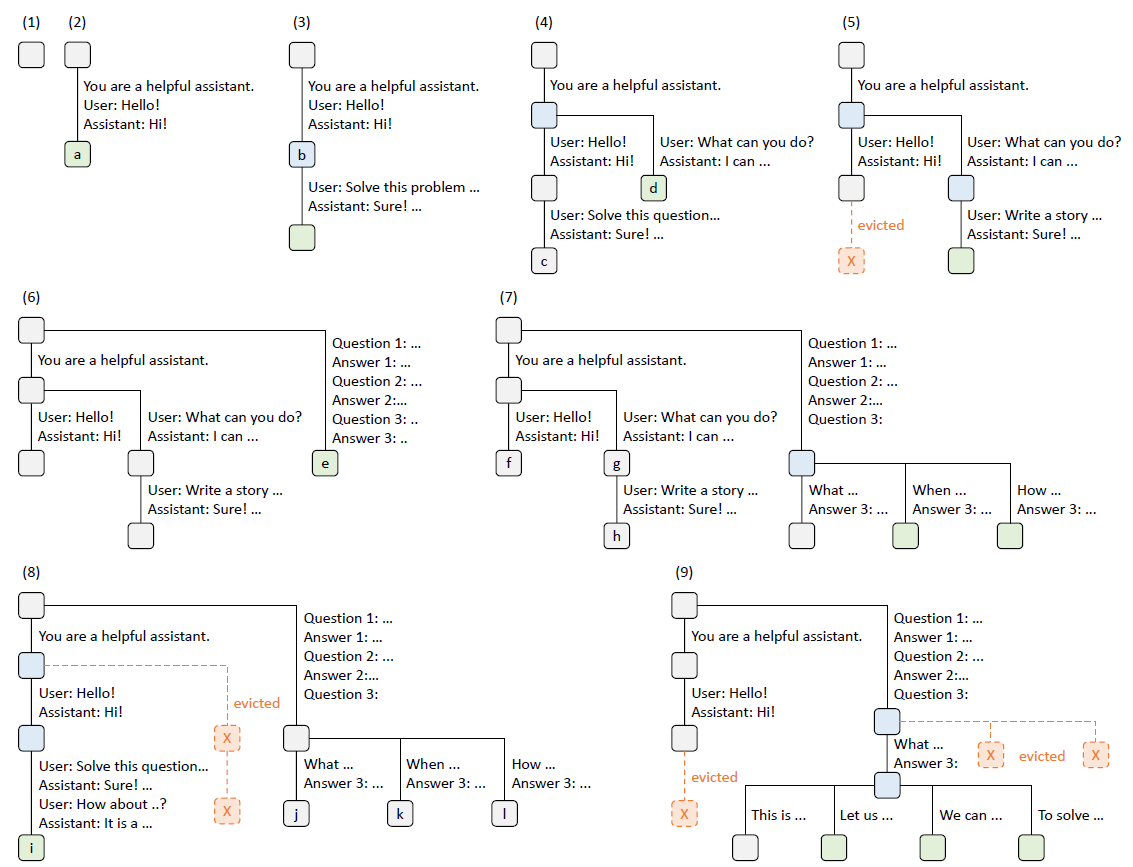
同样是使用树形存储,SGLang使用了Radix Tree结合LRU的存储策略(论文还有更多提高cache命中率之类的策略这里不予赘述)。所以其实核心就在Radix Tree和Prefix Tree的对比了。
像前缀树每个节点只能是单个Token,而Radix支持可变长的Token列表,因此可以节省大量节点指针是空间效率更高的存储模式,这里我们直接举个例子
存储以下键:"test", "team", "slow", "slowly"。
- Trie Tree
text
root
├─ t
│ ├─ e
│ │ ├─ s → t
│ │ └─ a → m
└─ s
└─ l → o → w
└─ l → y- Radix Tree
text
root
├─ te
│ ├─ "st" → [leaf: "test"]
│ └─ "am" → [leaf: "team"]
└─ "slow"
└─ "ly" → [leaf: "slowly"]整体上对比下ChunkAttention是固定长度的分块,树结构是静态的,对于类似超长systemt prompt、multiple few-shot、超长contxt的场景更加合适,因为能通过多chunk实现self-attention的并发计算。而Radix Attention基于Radix Tree,支持动态可变长的前缀,自然更适合类似多轮对话,multi-step思维链推理等动态前缀场景。
显式管理Cache:PML
- PROMPT CACHE: MODULAR ATTENTION REUSE FOR LOW-LATENCY INFERENCE
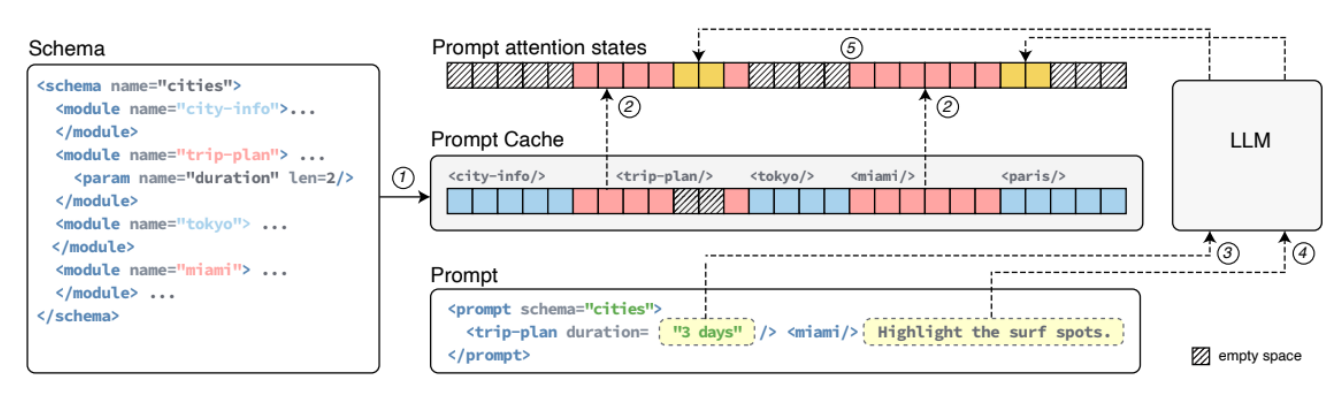
Prompt Cache则是提出了标记语言PML,支持用户显示标记输入内容中,哪些内容是需要被cache的。这里包含3个主要机制
- 通过XML语言标记的cache模块
如上图所示,每个module本身就是一个存储块,被XML包裹的内容会分别进行KV cache存储。下次在推理时会根据XML的tag进行对应Key,Value Tensor Cache的获取。
- 不连续的位置编码ID
但这就和前面的chunk Attention,Radix Attention有了显著的差异,就是PML支持非连续位置的缓存。这也引出了一个问题,只要不是从头开始的Prompt Cache,都会存在缓存cache的位置编码和使用该cache所在位置不同的问题。
论文给出的解释是他们经过实际测试,发现模型对非连续位置编码有包容性,只要cache的的模块内容部相对位置编码正确即可,即便下一次Cache出现的位置和它被缓存的绝对位置不同,也不会影响推理效果。但个人认为这依赖用户PML定义的极端合理化,也就是每个XML包裹的内容都是一个完整的语义内容,且彼此之间相对独立。例如多个few-shot使用这个模式就是可以的,一个system prompt里面<requirement>和<output foramt>用这种方式应该也可以。但要是放在多轮对话场景,或者multi-step思考推理场景,我感觉会出现问题。
- 缓存模块的拼接与新内容的计算
当一个用户提示由多个模块(有些是缓存的,有些是新的)组成时,Prompt Cache 会:
- 从缓存中检索已缓存模块的KV状态
- 对于提示中未被缓存的新文本段(比如插入到两个缓存模块之间的文本,或者在缓存模块之后的新文本),系统会根据它们在最终完整提示中的实际位置,为这些新文本段计算新的KV状态和相应的位置ID。例如,如果一段新文本插入在起始位置为0的模块A和起始位置为110的模块C之间,且模块A长度为50,那么这段新文本的位置ID将从50开始。
- 最后,系统将这些来自缓存的、带有原始(可能不从0开始)位置ID的KV状态,与新计算的、带有新分配位置ID的KV状态,按照它们在完整提示中的正确顺序拼接起来 。
VLLM源码分析
最后我们来直接看一个生产级别的源码实现。以下是VLLM中KV Cache的整个调用链路。整个调用链路如下
- 初始化阶段
- LLMEngine 初始化时调用 _initialize_kv_caches()
- Worker 通过 determine_num_available_blocks() 计算可用的 GPU 和 CPU 块数
- ModelRunner 初始化 KV 缓存配置
- BlockPool 创建并管理 KVCacheBlock 对象
- 推理阶段
- 客户端发送推理请求
- LLMEngine 接收请求并转发给 Worker
- Worker 调用 ModelRunner 执行模型推理
- ModelRunner 通过 KVCacheManager 获取或分配 KV 缓存块
- KVCacheManager 从 BlockPool 获取新的缓存块
- Attention 层使用 KV 缓存进行注意力计算
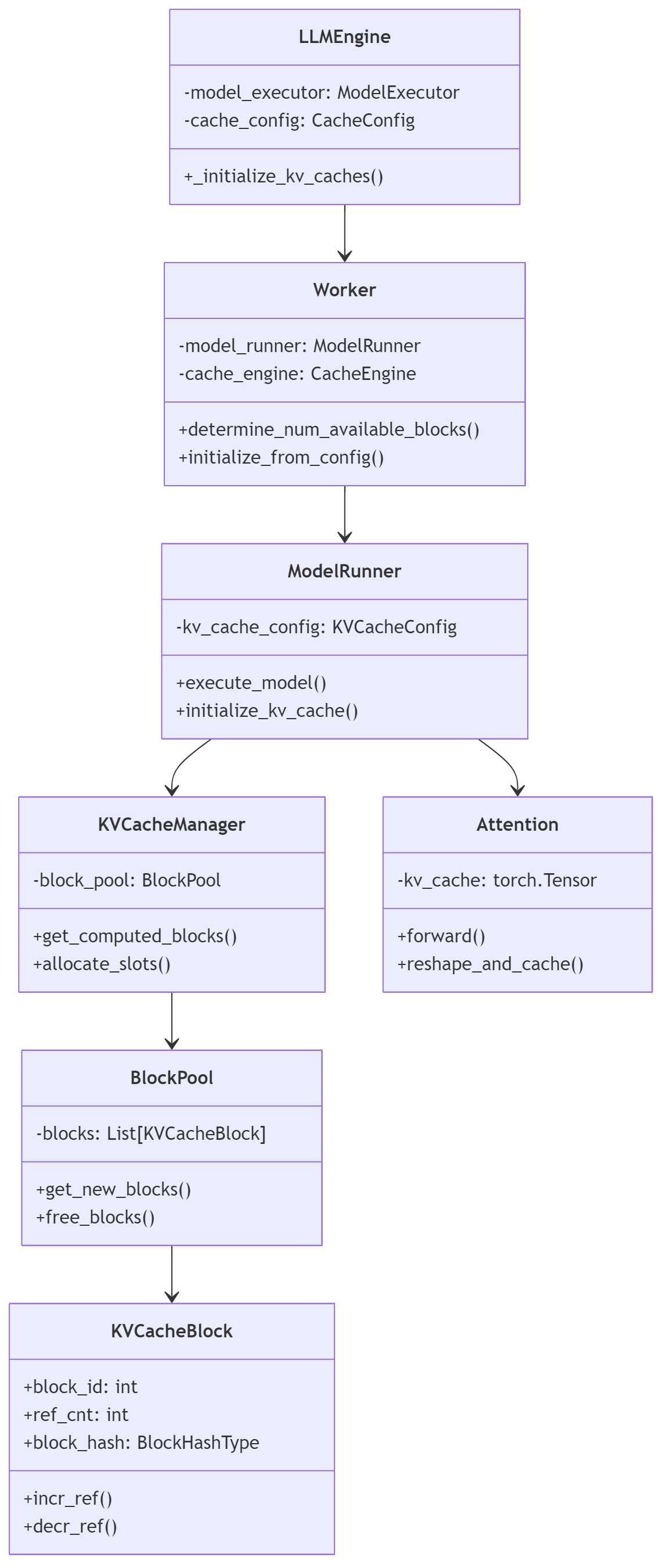
核心的KV Cache存储在KVCacheBlock类中,使用了和前面Chunk Attention相同的块存储机制,这里通过hash所有前缀token+当前块token得到block_hash
以下为cache存储、生成cache的哈希ID部分的核心代码。
python
@dataclass
class KVCacheBlock:
block_id: int
ref_cnt: int = 0
_block_hash: Optional[BlockHashType] = None
prev_free_block: Optional["KVCacheBlock"] = None
next_free_block: Optional["KVCacheBlock"] = None
def hash_block_tokens(
hash_function: Callable,
parent_block_hash: Optional[int],
curr_block_token_ids: Sequence[int],
extra_keys: Optional[tuple[Any, ...]] = None) -> BlockHashType:
"""计算块的哈希值,用于前缀缓存"""
if not parent_block_hash:
parent_block_hash = NONE_HASH
curr_block_token_ids_tuple = tuple(curr_block_token_ids)
return BlockHashType(
hash_function(
(parent_block_hash, curr_block_token_ids_tuple, extra_keys)),
curr_block_token_ids_tuple, extra_keys)VLLM还使用了Radix Attention的LRU最少使用驱逐策略,通过ref_cnt的引用计数追踪不使用的cache。同时当计数归0,cache不会直接被释放,而是会被添加到evictor,当内存压力大时再进行释放,保证更大程度的cache复用,避免频繁地内存分配和释放,相关驱逐代码如下
python
def _decr_refcount_cached_block(self, block: Block) -> None:
block_id = block.block_id
assert block_id is not None
refcount = self._refcounter.decr(block_id)
if refcount > 0:
block.block_id = None
return
else:
assert refcount == 0
# 将块添加到 evictor 而不是直接释放
self.evictor.add(block_id, block.content_hash,
block.num_tokens_total,
self._block_tracker[block_id].last_accessed)
class LRUEvictor(Evictor):
def evict(self) -> Tuple[int, int]:
while self.priority_queue:
last_accessed, _, block_id, content_hash = heapq.heappop(
self.priority_queue)
if (block_id in self.free_table and
self.free_table[block_id].last_accessed == last_accessed):
self.free_table.pop(block_id)
return block_id, content_hash当用户的Query进来,会按照固定chunk大小进行切分,然后从左到右进行去寻找cache,实现最长前缀命中。不过这里命中都是整个Block命中,也就是不会像Radix Tree一样支持Token级别的命中。命中前缀部分的代码如下
python
def find_longest_cache_hit(self, block_hashes: list[BlockHashType], max_length: int) -> list[KVCacheBlock]:
computed_blocks: list[KVCacheBlock] = []
max_num_blocks = max_length // self.block_size
for i in range(max_num_blocks):
block_hash = block_hashes[i]
if cached_block := self.block_pool.get_cached_block(block_hash):
computed_blocks.append(cached_block)
else:
break
if self.use_eagle and len(computed_blocks) > 0:
computed_blocks.pop()
return computed_blocks闭源 context Cache文档