注:本文为"向量点乘与叉乘"相关文章合辑。
图片清晰度受引文原图所限。
略作重排,未整理去重。
如有内容异常,请看原文。
向量点乘(内积)和叉乘(外积、向量积)概念及几何意义解读
-牧野- 于 2016-09-02 20:50:34 发布
一、向量基础概念
向量是由 n n n 个实数组成的一个 n n n 行 1 列( n × 1 n \times 1 n×1)或一个 1 行 n n n 列( 1 × n 1 \times n 1×n)的有序数组。
二、向量点乘(内积、数量积)
2.1 点乘定义
对两个向量执行点乘运算,就是对这两个向量对应位一一相乘之后求和的操作,点乘的结果是一个标量。
2.2 点乘公式
对于向量 a = [ a 1 , a 2 , ... , a n ] \mathbf{a} = [a_1, a_2, \dots, a_n] a=[a1,a2,...,an] 和向量 b = [ b 1 , b 2 , ... , b n ] \mathbf{b} = [b_1, b_2, \dots, b_n] b=[b1,b2,...,bn],
点积公式为:
a ⋅ b = a 1 b 1 + a 2 b 2 + ⋯ + a n b n \mathbf{a} \cdot \mathbf{b} = a_1b_1 + a_2b_2 + \dots + a_nb_n a⋅b=a1b1+a2b2+⋯+anbn
要求 :一维向量 a \mathbf{a} a 和 b \mathbf{b} b 的行列数相同。
2.3 点乘几何意义
点乘的几何意义是表征或计算两个向量之间的夹角,以及向量 b \mathbf{b} b 在向量 a \mathbf{a} a 方向上的投影。
公式为:
a ⋅ b = ∣ a ∣ ∣ b ∣ cos θ \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \cos\theta a⋅b=∣a∣∣b∣cosθ
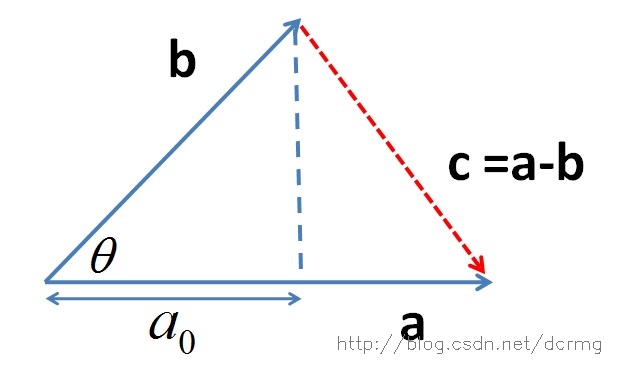
推导过程
- 定义向量 c = a − b \mathbf{c} = \mathbf{a} - \mathbf{b} c=a−b,根据三角形余弦定理:
c 2 = a 2 + b 2 − 2 ∣ a ∣ ∣ b ∣ cos θ \mathbf{c}^2 = \mathbf{a}^2 + \mathbf{b}^2 - 2|\mathbf{a}||\mathbf{b}|\cos\theta c2=a2+b2−2∣a∣∣b∣cosθ - 由向量运算 c = a − b \mathbf{c} = \mathbf{a} - \mathbf{b} c=a−b,可得:
( a − b ) ⋅ ( a − b ) = a ⋅ a + b ⋅ b − 2 a ⋅ b = a 2 + b 2 − 2 a ⋅ b (\mathbf{a} - \mathbf{b}) \cdot (\mathbf{a} - \mathbf{b}) = \mathbf{a} \cdot \mathbf{a} + \mathbf{b} \cdot \mathbf{b} - 2\mathbf{a} \cdot \mathbf{b} = \mathbf{a}^2 + \mathbf{b}^2 - 2\mathbf{a} \cdot \mathbf{b} (a−b)⋅(a−b)=a⋅a+b⋅b−2a⋅b=a2+b2−2a⋅b - 结合上述两式得:
a 2 + b 2 − 2 a ⋅ b = a 2 + b 2 − 2 ∣ a ∣ ∣ b ∣ cos θ \mathbf{a}^2 + \mathbf{b}^2 - 2\mathbf{a} \cdot \mathbf{b} = \mathbf{a}^2 + \mathbf{b}^2 - 2|\mathbf{a}||\mathbf{b}|\cos\theta a2+b2−2a⋅b=a2+b2−2∣a∣∣b∣cosθ
化简后即得:
a ⋅ b = ∣ a ∣ ∣ b ∣ cos θ \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}||\mathbf{b}|\cos\theta a⋅b=∣a∣∣b∣cosθ
向量 a \mathbf{a} a, b \mathbf{b} b 的长度都是可以计算的已知量,从而有 a \mathbf{a} a 和 b \mathbf{b} b 间的夹角 θ \theta θ:
利用公式
θ = arccos ( a ⋅ b ∣ a ∣ ∣ b ∣ ) \theta = \arccos\left(\frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a}||\mathbf{b}|}\right) θ=arccos(∣a∣∣b∣a⋅b)
可确定向量 a \mathbf{a} a 与 b \mathbf{b} b 的夹角 θ \theta θ(其中 0 ∘ ≤ θ ≤ 180 ∘ 0^\circ \leq \theta \leq 180^\circ 0∘≤θ≤180∘)及方向关系:
- a ⋅ b > 0 \mathbf{a} \cdot \mathbf{b} > 0 a⋅b>0:夹角 0 ∘ ≤ θ < 90 ∘ 0^\circ \leq \theta < 90^\circ 0∘≤θ<90∘(或 0 ≤ θ < π 2 0 \leq \theta < \frac{\pi}{2} 0≤θ<2π),方向具有正相关性;
- a ⋅ b = 0 \mathbf{a} \cdot \mathbf{b} = 0 a⋅b=0:夹角 90 ∘ 90^\circ 90∘(或 π 2 \frac{\pi}{2} 2π),两向量正交(垂直);
- a ⋅ b < 0 \mathbf{a} \cdot \mathbf{b} < 0 a⋅b<0:夹角 90 ∘ < θ ≤ 180 ∘ 90^\circ < \theta \leq 180^\circ 90∘<θ≤180∘(或 π 2 < θ ≤ π \frac{\pi}{2} < \theta \leq \pi 2π<θ≤π),方向具有负相关性。
补充说明:如果 a \mathbf{a} a 或 b \mathbf{b} b 中至少有一个是零向量,则该公式不适用。通常约定,零向量与任何向量的夹角都是任意的。
三、向量叉乘(外积、向量积)
3.1 叉乘定义
两个向量的叉乘运算结果是一个向量,且该向量与这两个向量组成的坐标平面垂直。
3.2 叉乘公式
对于三维向量 a = ( x 1 , y 1 , z 1 ) \mathbf{a} = (x_1, y_1, z_1) a=(x1,y1,z1) 和 b = ( x 2 , y 2 , z 2 ) \mathbf{b} = (x_2, y_2, z_2) b=(x2,y2,z2),
叉乘公式为:
a × b = ∣ i j k x 1 y 1 z 1 x 2 y 2 z 2 ∣ = ( y 1 z 2 − y 2 z 1 ) i − ( x 1 z 2 − x 2 z 1 ) j + ( x 1 y 2 − x 2 y 1 ) k \mathbf{a} \times \mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{vmatrix} = (y_1z_2 - y_2z_1)\mathbf{i} - (x_1z_2 - x_2z_1)\mathbf{j} + (x_1y_2 - x_2y_1)\mathbf{k} a×b= ix1x2jy1y2kz1z2 =(y1z2−y2z1)i−(x1z2−x2z1)j+(x1y2−x2y1)k
其中, i = ( 1 , 0 , 0 ) \mathbf{i} = (1, 0, 0) i=(1,0,0), j = ( 0 , 1 , 0 ) \mathbf{j} = (0, 1, 0) j=(0,1,0), k = ( 0 , 0 , 1 ) \mathbf{k} = (0, 0, 1) k=(0,0,1) 为单位向量。
叉乘结果也可表示为坐标形式:
a × b = ( y 1 z 2 − y 2 z 1 , − ( x 1 z 2 − x 2 z 1 ) , x 1 y 2 − x 2 y 1 ) \mathbf{a} \times \mathbf{b} = (y_1z_2 - y_2z_1, -(x_1z_2 - x_2z_1), x_1y_2 - x_2y_1) a×b=(y1z2−y2z1,−(x1z2−x2z1),x1y2−x2y1)
3.3 叉乘几何意义
-
三维空间 :
叉乘结果是垂直于 a \mathbf{a} a 和 b \mathbf{b} b 构成平面的法向量,常用于构建三维坐标系(如 X、Y、Z 轴)。
- 性质: b × a = − a × b \mathbf{b} \times \mathbf{a} = -\mathbf{a} \times \mathbf{b} b×a=−a×b(叉乘结果方向相反)。
-
二维空间 :
叉乘的绝对值等于由向量 a \mathbf{a} a 和 b \mathbf{b} b 构成的平行四边形的面积,即:
∣ a × b ∣ = 平行四边形面积 |\mathbf{a} \times \mathbf{b}| = \text{平行四边形面积} ∣a×b∣=平行四边形面积
向量叉乘
Sunomg 于 2017-04-19 15:00:02 发布
一、向量叉乘公式及推导
对于三维向量 a = ( x 1 , y 1 , z 1 ) \mathbf{a} = (x_1, y_1, z_1) a=(x1,y1,z1) 和 b = ( x 2 , y 2 , z 2 ) \mathbf{b} = (x_2, y_2, z_2) b=(x2,y2,z2),
i = ( 1 , 0 , 0 ) \mathbf{i} = (1, 0, 0) i=(1,0,0)、 j = ( 0 , 1 , 0 ) \mathbf{j} = (0, 1, 0) j=(0,1,0)、 k = ( 0 , 0 , 1 ) \mathbf{k} = (0, 0, 1) k=(0,0,1) 为三维空间的标准正交基向量;
叉乘公式通过行列式展开计算:
a × b = ∣ i j k x 1 y 1 z 1 x 2 y 2 z 2 ∣ = i ( y 1 z 2 − y 2 z 1 ) − j ( x 1 z 2 − x 2 z 1 ) + k ( x 1 y 2 − x 2 y 1 ) = ( y 1 z 2 − y 2 z 1 , − ( x 1 z 2 − x 2 z 1 ) , x 1 y 2 − x 2 y 1 ) \begin{aligned} \mathbf{a} \times \mathbf{b} &= \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{vmatrix} \\[1em] &= \mathbf{i}(y_1 z_2 - y_2 z_1) - \mathbf{j}(x_1 z_2 - x_2 z_1) + \mathbf{k}(x_1 y_2 - x_2 y_1) \\[1em] &= (y_1 z_2 - y_2 z_1, -(x_1 z_2 - x_2 z_1), x_1 y_2 - x_2 y_1) \end{aligned} a×b= ix1x2jy1y2kz1z2 =i(y1z2−y2z1)−j(x1z2−x2z1)+k(x1y2−x2y1)=(y1z2−y2z1,−(x1z2−x2z1),x1y2−x2y1)
说明:
- 行列式展开时遵循"对角线法则",符号由基向量的排列顺序决定(如 j \mathbf{j} j 分量前带负号)。

二、向量叉乘的几何意义
- 三维空间特性
叉乘结果 a × b \mathbf{a} \times \mathbf{b} a×b 是一个法向量 ,满足:- 垂直于 a \mathbf{a} a 和 b \mathbf{b} b 构成的平面;
- 方向由右手定则 确定:右手四指从 a \mathbf{a} a 转向 b \mathbf{b} b(小于 180 ∘ 180^\circ 180∘ 的夹角),拇指方向即为叉乘向量方向。
- 反交换律: b × a = − a × b \mathbf{b} \times \mathbf{a} = -\mathbf{a} \times \mathbf{b} b×a=−a×b(方向相反)。

- 模长的几何含义
叉乘向量的模长等于以 a \mathbf{a} a 和 b \mathbf{b} b 为邻边的平行四边形面积:
∣ a × b ∣ = ∣ a ∣ ⋅ ∣ b ∣ ⋅ sin θ ( θ 为两向量夹角 ) |\mathbf{a} \times \mathbf{b}| = |\mathbf{a}| \cdot |\mathbf{b}| \cdot \sin\theta \quad (\theta \text{ 为两向量夹角}) ∣a×b∣=∣a∣⋅∣b∣⋅sinθ(θ 为两向量夹角)
三、向量叉乘的应用
3.1 三维模型中法向量计算
通过三角面的两条邻边向量(如 A B → \overrightarrow{AB} AB 和 A C → \overrightarrow{AC} AC )叉乘,可得到垂直于该三角面的法向量,用于光照计算、网格渲染等场景。
3.2 判断向量顺逆关系(二维场景)
设向量 P = ( x p , y p ) \mathbf{P} = (x_p, y_p) P=(xp,yp), Q = ( x q , y q ) \mathbf{Q} = (x_q, y_q) Q=(xq,yq),计算叉积(二维可视为三维 z z z 分量为 0 的特例):
P × Q = x p y q − x q y p \mathbf{P} \times \mathbf{Q} = x_p y_q - x_q y_p P×Q=xpyq−xqyp
- 若 P × Q > 0 \mathbf{P} \times \mathbf{Q} > 0 P×Q>0: P \mathbf{P} P 在 Q \mathbf{Q} Q 的逆时针方向(绕原点);
- 若 P × Q < 0 \mathbf{P} \times \mathbf{Q} < 0 P×Q<0: P \mathbf{P} P 在 Q \mathbf{Q} Q 的顺时针方向;
- 若 P × Q = 0 \mathbf{P} \times \mathbf{Q} = 0 P×Q=0: P \mathbf{P} P 与 Q \mathbf{Q} Q 共线。
3.3 凸多边形与凹多边形判断
对多边形的每条边 e i \mathbf{e}i ei 和 e i + 1 \mathbf{e}{i+1} ei+1 构成的向量进行叉积计算:
- 若所有叉积结果同号(均 > 0 或均 < 0) :多边形为凸多边形;
- 若存在叉积结果异号 :多边形为凹多边形;
- 若所有叉积结果均为 0 :多边形顶点共线(退化为线段)。
3.4 判断点与直线的位置关系
在直线上取两点 A ( x 1 , y 1 ) A(x_1, y_1) A(x1,y1)、 B ( x 2 , y 2 ) B(x_2, y_2) B(x2,y2),待判断点 P ( x 0 , y 0 ) P(x_0, y_0) P(x0,y0),构造向量:
A B → = ( x 2 − x 1 , y 2 − y 1 ) , A P → = ( x 0 − x 1 , y 0 − y 1 ) \overrightarrow{AB} = (x_2 - x_1, y_2 - y_1), \quad \overrightarrow{AP} = (x_0 - x_1, y_0 - y_1) AB =(x2−x1,y2−y1),AP =(x0−x1,y0−y1)
计算叉积:
A B → × A P → = ( x 2 − x 1 ) ( y 0 − y 1 ) − ( y 2 − y 1 ) ( x 0 − x 1 ) \overrightarrow{AB} \times \overrightarrow{AP} = (x_2 - x_1)(y_0 - y_1) - (y_2 - y_1)(x_0 - x_1) AB ×AP =(x2−x1)(y0−y1)−(y2−y1)(x0−x1)
- 若结果 = 0:点 P P P 在直线 A B AB AB 上;
- 若结果 > 0:点 P P P 在直线 A B AB AB 的一侧(由叉积符号决定具体方向);
- 若结果 < 0:点 P P P 在直线 A B AB AB 的另一侧。
3.5 点与矩形的位置关系判断(需结合坐标范围)
通过叉乘判断点是否在矩形各边的内侧,或直接比较点坐标与矩形边界的范围(更高效)。
说明:
- 原文中"叉积和"表述易混淆,已修正为"叉积的标量结果"或"叉积分量";
- 公式中的排版错误(如 y 1 z 2 − y_{1} z_{2-} y1z2−)已修正为标准下标格式 y 1 z 2 − y 2 z 1 y_1 z_2 - y_2 z_1 y1z2−y2z1;
- 二维场景下的叉乘可视为三维叉乘在 z = 0 z=0 z=0 平面的投影,结果的符号反映旋转方向。
向量点乘与叉乘的概念及几何意义
作者:Plane 老师 编辑时间:2022-07-08 23:23
一、向量点乘(内积)
1.1 定义与公式
点乘(Dot Product) ,又称数量积 或标量积(Scalar Product),其结果为标量。
代数定义:
对于空间向量 a ⃗ = ( x 1 , y 1 , z 1 ) \vec{a} = (x_1, y_1, z_1) a =(x1,y1,z1) 和 b ⃗ = ( x 2 , y 2 , z 2 ) \vec{b} = (x_2, y_2, z_2) b =(x2,y2,z2),点乘运算为对应分量乘积之和:
a ⃗ ⋅ b ⃗ = x 1 x 2 + y 1 y 2 + z 1 z 2 \vec{a} \cdot \vec{b} = x_1x_2 + y_1y_2 + z_1z_2 a ⋅b =x1x2+y1y2+z1z2
几何定义:
点乘等于两向量的模长与夹角余弦值的乘积:
a ⃗ ⋅ b ⃗ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ cos θ \vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos\theta a ⋅b =∣a ∣∣b ∣cosθ
其中 θ \theta θ 为 a ⃗ \vec{a} a 与 b ⃗ \vec{b} b 的夹角。
1.2 几何意义
点乘结果表示 a ⃗ \vec{a} a 在 b ⃗ \vec{b} b 方向上的投影 与 ∣ b ⃗ ∣ |\vec{b}| ∣b ∣ 的乘积,反映两向量的方向相似度。根据结果符号可判断向量关系:
- a ⃗ ⋅ b ⃗ > 0 \vec{a} \cdot \vec{b} > 0 a ⋅b >0:方向基本相同,夹角 0 ∘ < θ < 90 ∘ 0^\circ < \theta < 90^\circ 0∘<θ<90∘;
- a ⃗ ⋅ b ⃗ = 0 \vec{a} \cdot \vec{b} = 0 a ⋅b =0:两向量正交(垂直);
- a ⃗ ⋅ b ⃗ < 0 \vec{a} \cdot \vec{b} < 0 a ⋅b <0:方向基本相反,夹角 90 ∘ < θ < 180 ∘ 90^\circ < \theta < 180^\circ 90∘<θ<180∘。
示意图 :
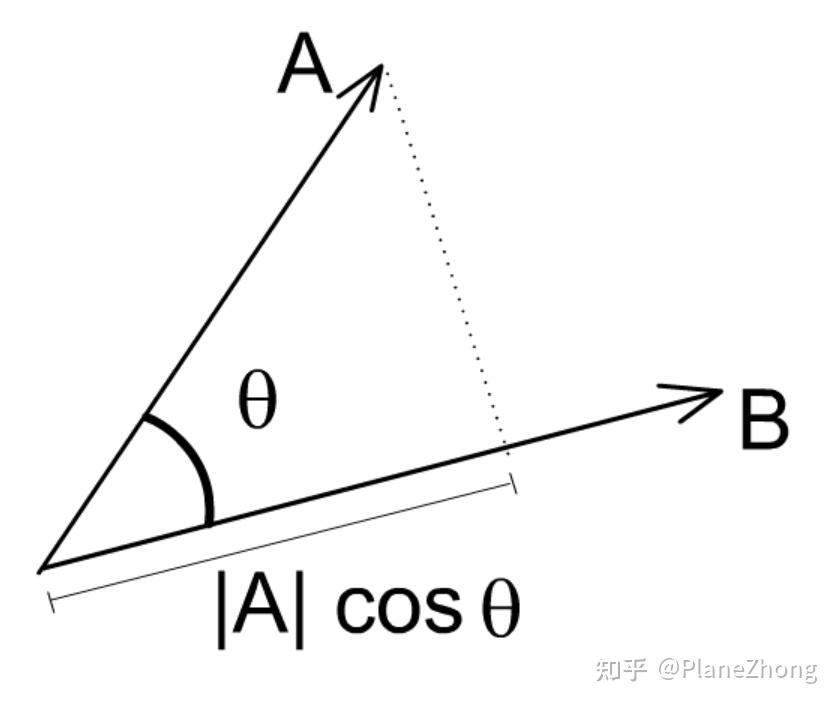
1.3 代数定义推导几何定义(夹角公式推导)
设定:
- 向量 a ⃗ \vec{a} a 终点为 A ( x 1 , y 1 , z 1 ) A(x_1, y_1, z_1) A(x1,y1,z1), b ⃗ \vec{b} b 终点为 B ( x 2 , y 2 , z 2 ) B(x_2, y_2, z_2) B(x2,y2,z2),原点为 O O O;
- 向量 A B ⃗ = ( x 2 − x 1 , y 2 − y 1 , z 2 − z 1 ) \vec{AB} = (x_2 - x_1, y_2 - y_1, z_2 - z_1) AB =(x2−x1,y2−y1,z2−z1)。
推导过程:
- 在 △ O A B \triangle OAB △OAB 中,由余弦定理:
∣ A B ⃗ ∣ 2 = ∣ a ⃗ ∣ 2 + ∣ b ⃗ ∣ 2 − 2 ∣ a ⃗ ∣ ∣ b ⃗ ∣ cos θ |\vec{AB}|^2 = |\vec{a}|^2 + |\vec{b}|^2 - 2|\vec{a}||\vec{b}|\cos\theta ∣AB ∣2=∣a ∣2+∣b ∣2−2∣a ∣∣b ∣cosθ - 代入距离公式 ∣ A B ⃗ ∣ 2 = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + ( z 2 − z 1 ) 2 |\vec{AB}|^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2 ∣AB ∣2=(x2−x1)2+(y2−y1)2+(z2−z1)2,展开并整理得:
∣ a ⃗ ∣ ∣ b ⃗ ∣ cos θ = x 1 2 + y 1 2 + z 1 2 + x 2 2 + y 2 2 + z 2 2 − [ ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + ( z 2 − z 1 ) 2 ] 2 |\vec{a}||\vec{b}|\cos\theta = \frac{x_1^2 + y_1^2 + z_1^2 + x_2^2 + y_2^2 + z_2^2 - [(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2]}{2} ∣a ∣∣b ∣cosθ=2x12+y12+z12+x22+y22+z22−[(x2−x1)2+(y2−y1)2+(z2−z1)2] - 去括号化简后:
∣ a ⃗ ∣ ∣ b ⃗ ∣ cos θ = x 1 x 2 + y 1 y 2 + z 1 z 2 = a ⃗ ⋅ b ⃗ |\vec{a}||\vec{b}|\cos\theta = x_1x_2 + y_1y_2 + z_1z_2 = \vec{a} \cdot \vec{b} ∣a ∣∣b ∣cosθ=x1x2+y1y2+z1z2=a ⋅b
夹角公式 :
θ = arccos ( a ⃗ ⋅ b ⃗ ∣ a ⃗ ∣ ∣ b ⃗ ∣ ) \theta = \arccos\left(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|}\right) θ=arccos(∣a ∣∣b ∣a ⋅b )
二、向量叉乘(外积)
2.1 定义与公式
叉乘(Cross Product) ,又称向量积(Vector Product),其结果为向量,且与原向量所在平面垂直。
代数定义(三维向量) :
对于向量 a ⃗ = ( x 1 , y 1 , z 1 ) \vec{a} = (x_1, y_1, z_1) a =(x1,y1,z1) 和 b ⃗ = ( x 2 , y 2 , z 2 ) \vec{b} = (x_2, y_2, z_2) b =(x2,y2,z2),叉乘可通过行列式计算:
a ⃗ × b ⃗ = ∣ i ⃗ j ⃗ k ⃗ x 1 y 1 z 1 x 2 y 2 z 2 ∣ = ( y 1 z 2 − z 1 y 2 , z 1 x 2 − x 1 z 2 , x 1 y 2 − y 1 x 2 ) \vec{a} \times \vec{b} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{vmatrix} = (y_1z_2 - z_1y_2, \ z_1x_2 - x_1z_2, \ x_1y_2 - y_1x_2) a ×b = i x1x2j y1y2k z1z2 =(y1z2−z1y2, z1x2−x1z2, x1y2−y1x2)
其中 i ⃗ , j ⃗ , k ⃗ \vec{i}, \vec{j}, \vec{k} i ,j ,k 为三维单位正交基向量。
几何定义 :
叉乘结果为垂直于 a ⃗ \vec{a} a 和 b ⃗ \vec{b} b 的法向量,其模长与方向满足:
a ⃗ × b ⃗ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ sin θ ⋅ n ⃗ \vec{a} \times \vec{b} = |\vec{a}| |\vec{b}| \sin\theta \cdot \vec{n} a ×b =∣a ∣∣b ∣sinθ⋅n
- n ⃗ \vec{n} n 为 a ⃗ \vec{a} a 和 b ⃗ \vec{b} b 所在平面的单位法向量;
- 方向由右手定则 确定:右手四指从 a ⃗ \vec{a} a 转向 b ⃗ \vec{b} b (夹角 < 180 ∘ < 180^\circ <180∘),拇指方向即为叉乘向量方向。
示意图:
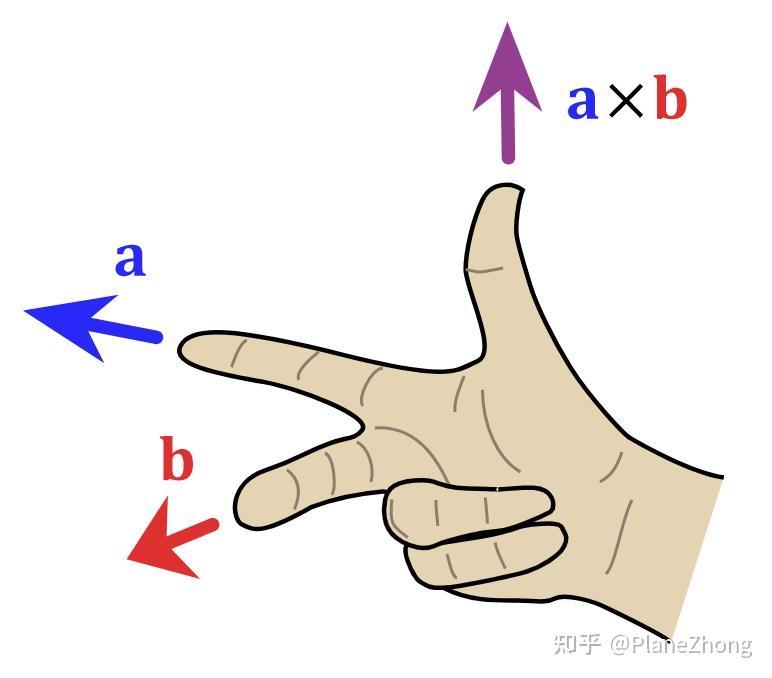
2.2 几何意义
- 模长的几何含义 :
叉乘向量的模长等于以 a ⃗ \vec{a} a 和 b ⃗ \vec{b} b 为邻边的平行四边形面积:
∣ a ⃗ × b ⃗ ∣ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ sin θ |\vec{a} \times \vec{b}| = |\vec{a}| |\vec{b}| \sin\theta ∣a ×b ∣=∣a ∣∣b ∣sinθ - 方向的几何含义 :
结果向量是 a ⃗ \vec{a} a 和 b ⃗ \vec{b} b 所在平面的法线向量,常用于三维空间中法向量的计算(如平面方程、光照模型等)。
示意图:
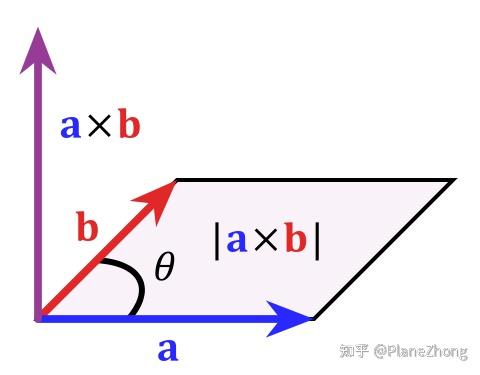
via:
- 向量点乘(内积)和叉乘(外积、向量积)概念及几何意义解读-CSDN博客
https://blog.csdn.net/dcrmg/article/details/52416832 - 向量叉乘与应用-CSDN博客
https://blog.csdn.net/Sunomg/article/details/70240886 - 带你一次搞懂点积(内积)、叉积(外积)-CSDN博客
https://blog.csdn.net/apr15/article/details/106160407 -
向量点乘与叉乘的概念及几何意义 - 知乎
https://zhuanlan.zhihu.com/p/359975221 - 向量运算详解-CSDN博客
https://blog.csdn.net/qq_38182397/article/details/80508303 - 点积与叉积详解-CSDN博客
https://blog.csdn.net/itworld123/article/details/79083587 -
【数学计算】点乘/点积/内积/数量积/叉乘/外积/叉积/向量积-CSDN博客
https://blog.csdn.net/baidu_35692628/article/details/128460826 - 【数学计算】判断两条线段是否相交+计算两条线段的交点和夹角_判断两线段是否相交,并求交点-CSDN博客
https://blog.csdn.net/baidu_35692628/article/details/127201071