1 简介

⽐特币基于椭圆曲线加密的椭圆曲线数字签名算法（ECDSA），特定的椭圆曲线称为secp256k1。其公式定义如下

y²=x³+ax+b mod p

其中：p = 0xFFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F = 2²⁵⁶-2³²-2⁹-2⁸-2⁷-2⁶-2⁴-1 = 2²⁵⁶-2³²-977，a = 0, b=7

基点G为：x=0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798，y=0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8

G的阶为：n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141

secp256k1的命名出自一个密码协议标准，每一个字母和数字都代表着特定含义，下面分别进行介绍

1.1 密码协议标准

第一部分是「sec」，sec是Standards for Efficient Cryptography 的简称，是SECG发布的一种密码学协议标准。SECG发布的「SEC 1」和「SEC 2」两个关于椭圆曲线的协议标准，在「SEC 2」中有详细说明secp256k1以及其他曲线的参数定义。除了「sec」，还有众多其他关于椭圆曲线的协议标准，从SafeCurve中可以看到有下列不同类型的标准。

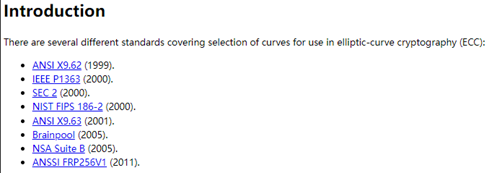
「SafeCurve」此处较久没有更新，有些标准已经更新了多次，例如NIST关于数字签名的标准 FIPS 186目前在用的是第四版，第五版也在起草中了，从「NIST」官网中可见。

1.2 有限域

第二部分是「p」，p表示该椭圆曲线是基于素数有限域F_p。有限域是离散数学中的概念，它是一个由有限数量元素组成的集合，元素之间可以进行加法和乘法计算。密码学中使用椭圆曲线都是基于有限域的，除了素数有限域F_p之外，还有另一种特征为2的有限域F₂^m，F_p的大小（元素个数）为p，F₂^m的大小为2^m。基于F_p的椭圆曲线为：

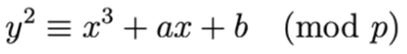
基于F₂^m的椭圆曲线为：

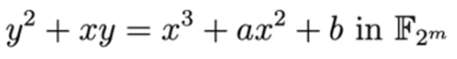
在「SEC 2」中还定义了sect163k1、sect163r1等曲线，其中，t表示的是该曲线基于F₂^m。在「NIST FIPS 186-4」中定了P-256、B-163等曲线，P-表示基于F_p，B-表示基于F₂^m。

1.3 有限域大小

每个椭圆曲线E都有若干关键参数，包括阶为n的基点G和协因子h等，其中，n为一个大素数，n*h为椭圆曲线上点的数量。为了计算效率考虑，h通常设置为1、2或4。通俗地讲，如果椭圆曲线上的点数量越多，那么这条椭圆曲线的安全度就越高，因此n的取值是影响曲线安全的关键。椭圆曲线又都是基于有限域的，曲线上的点都是有限域中的元素，因此，有限域大小决定了曲线安全度。第三部分「256」就是有限域大小的表现形式，还有更多其他如192、224、384等，在「NIST FIPS 186-4」中有个表格展现了F_p 和F₂^m两个域的各种不同大小配置。

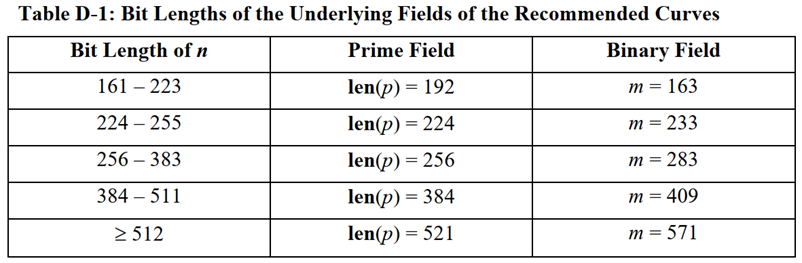
SEC标准在这块的设置和NIST标准类似，我们会看到p系列的曲线有p192、p224、p256（secp256k1就是其中一种）、p384和p521，t/B系列有t163/B-163、t233/B-233等。

1.4 Koblitz Curve

第四部分「k」表示该曲线是Koblitz Curve（科布利兹曲线），从「SEC 2」中可以看到还有此处标记为r的曲线（如secp256r1），r表示该曲线是伪随机曲线Pseudo-Random Curve。Koblitz Curve命名源自数学家「Neal Koblitz」，它是一种特殊的曲线，它的一些参数是精心挑选设置的。Koblitz Curve具有自同态的性质，可以通过优化大幅提升计算效率。相比之下，Pesudo-Random Curve的对应参数是通过随机种子计算出来的，有标准的检验算法可以检测所有参数是随机种子产生而来。在「NIST FIPS 186-4」中Koblitz Curve曲线以「K-」标记开头，分别有K-163、K-233等。

1.5 末位标记

到了第五部分「1」，这是代表在前4个条件下提供了多种推荐参数设置，在SEC标准中大部分该位都是1，即只提供一种推荐参数，sect163r2是一个例外。下面把SEC和NIST两个标准推荐的曲线分别列一下，二者有较大部分是相同的参数设置。

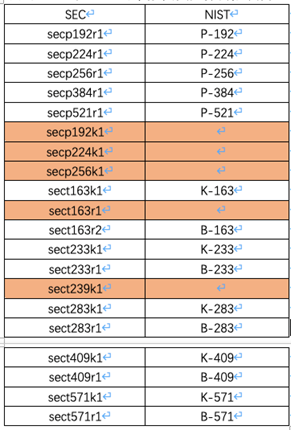
上述表格中，同一行中SEC和NIST都出现的，两个曲线虽然名字不同，但参数完全相同，也就是说其实一样的。橙色底纹的几个SEC曲线没有对应的NIST曲线，因此SEC标准包含的曲线比NIST多一些，如这里secp256k1就是SEC标准单独存在的。说到这里，不得不提一个正经八卦。据说，NIST推荐的Pesudo-Random Curve，也就是P和B系列，并没有公布随机数挑选规则，外界存在一种疑虑，可能NSA（美国国家安全局）掌握了后门，能够轻易破解这些密码协议。

2 源码及编译

secp256k1源码可以从以下地址下载：https://github.com/bitcoin-core/secp256k1

用git下载源码

复制代码

git clone https://github.com/bitcoin-core/secp256k1

Check out最新release版本

复制代码

git checkout v0.6.0

2.1 Linux下编译

在Linux下可以使用Autotools进行编译

复制代码

$ ./autogen.sh       # Generate a ./configure script
$ ./configure        # Generate a build system
$ make               # Run the actual build process
$ make check         # Run the test suite
$ sudo make install  # Install the library into the system (optional)

可以用./configure --prefix=指定安装路径，如我将编译结果安装到buildout目录下，其目录结构如下：

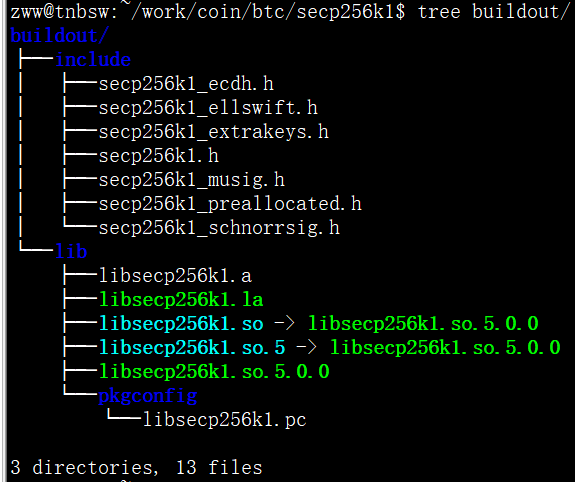
2.2 Windows编译

在Windows下，使用CMake+VS2019进行编译，编译配置如下：

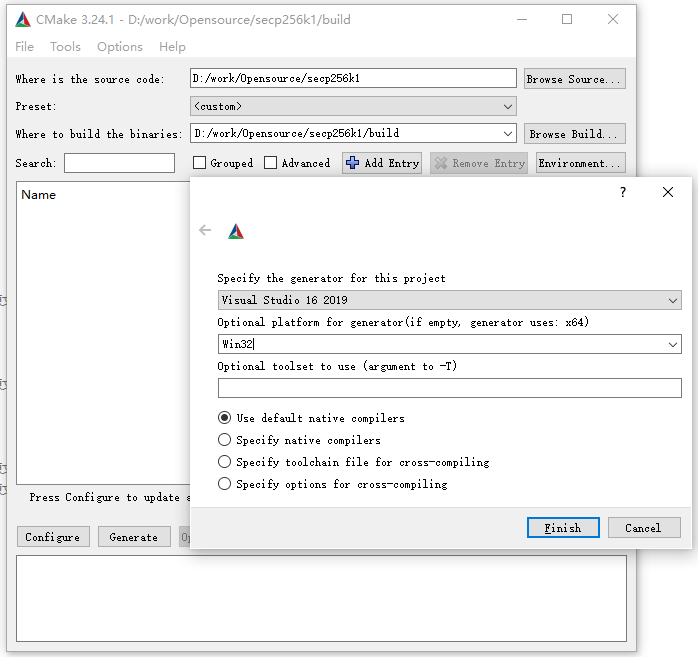
Generate时使用默认配置，完成后用VS2019打开生成好的工程，进行编译，结果如下：

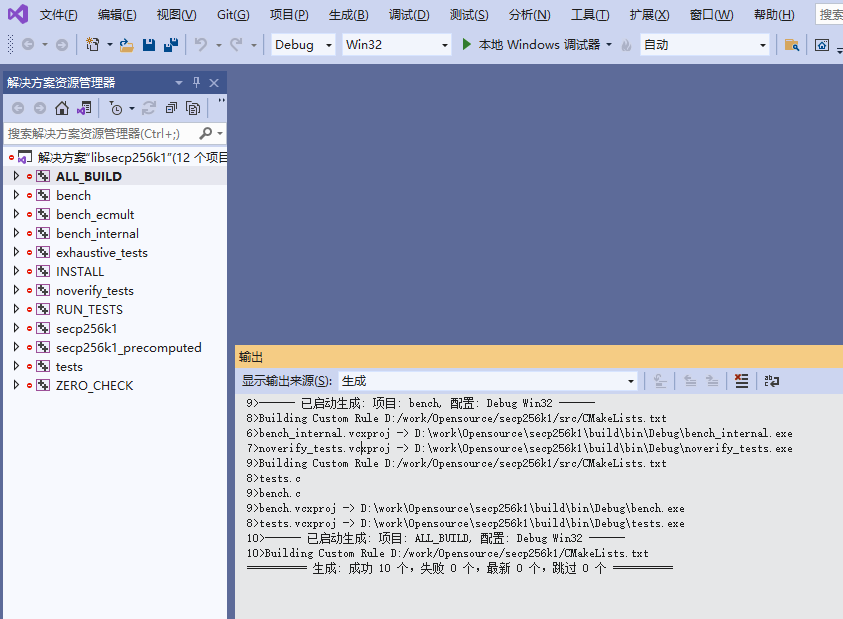
运行其中的tests项目输出如下：

由于内容比较多，所以运行花费时间较长。

3 应用

用VS2019创建控制台应用程序secp256k1Test，并将include和之前编译生成lib库及dll库放到工程目录下

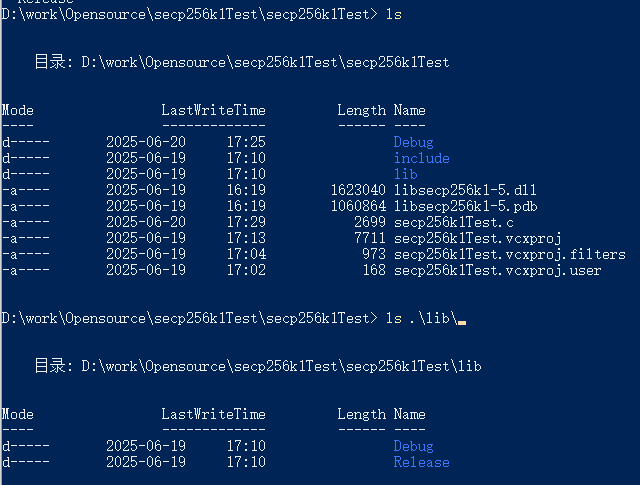
按照以上目录结构，修改项目C/C++中的包含路径及链接器中的配置

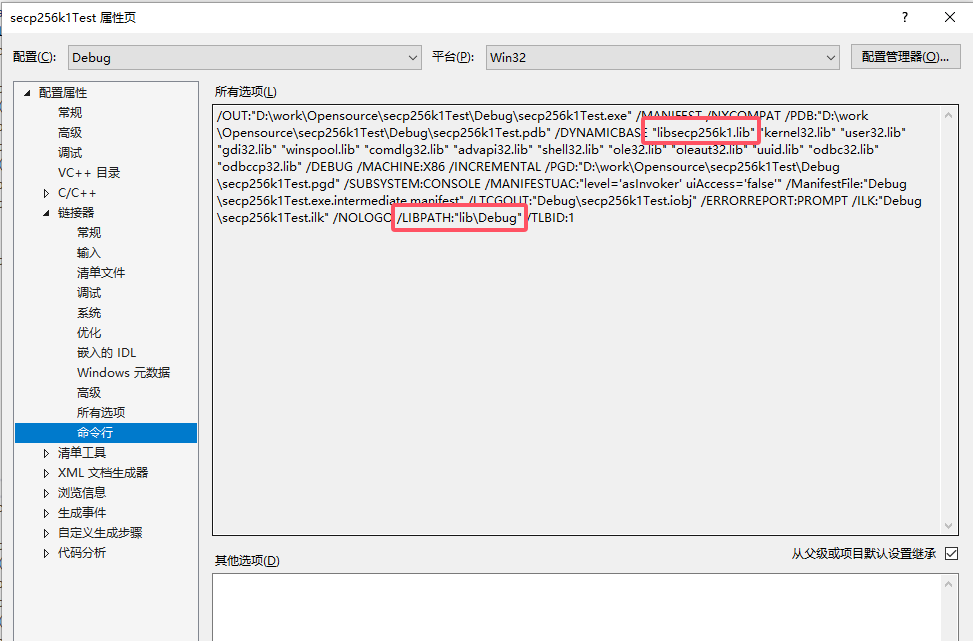
主程序secp256k1Test.c如下

复制代码

 1 #include <stdlib.h>
 2 #include <stdio.h>
 3 #include <string.h>
 4 #include <stdint.h>
 5 #include "secp256k1.h"
 6 
 7 #define    bswap_16(value)  \
 8     ((((value) & 0xff) << 8) | ((value) >> 8))
 9 
10 #define    bswap_32(value)    \
11     (((uint32_t)bswap_16((uint16_t)((value) & 0xffff)) << 16) | \
12     (uint32_t)bswap_16((uint16_t)((value) >> 16)))
13 
14 #define    bswap_64(value)    \
15     (((uint64_t)bswap_32((uint32_t)((value) & 0xffffffff)) \
16     << 32) | \
17     (uint64_t)bswap_32((uint32_t)((value) >> 32)))
18 
19 int main()
20 {
21     int ret;
22     secp256k1_context* pCtx = NULL;
23     secp256k1_pubkey pubkey;
24     unsigned char rand32[32] = { 0 };
25     printf("this is for secp256k1 testing\n");
26     
27     pCtx = secp256k1_context_create(SECP256K1_CONTEXT_NONE);
28     if (pCtx) {
29         for (int i = 0; i < sizeof(rand32) / 4; i++) {
30             int r = rand();
31             memcpy(rand32 + i * 4, &r, 4);
32         }
33         if (!secp256k1_context_randomize(pCtx, rand32))
34             printf("secp256k1_context_randomize failed\n");
35         else {
36             printf("secp256k1_context_randomize success\n");
37         }
38 
39         memset(rand32, 0, sizeof(rand32));
40         rand32[31] = 1;
41         ret = secp256k1_ec_pubkey_create(pCtx, &pubkey, rand32);
42         if (ret) {
43             printf("private key\n0x");
44             for (int i = 0; i < 32; i++)
45                 printf("%02x", rand32[i]);
46             printf("\n");
47             printf("secp256k1_ec_pubkey_create success\n");
48             printf("0x");
49             for (int i = 0; i < 32; i++)
50                 printf("%02x", pubkey.data[31-i]);
51             printf("\n0x");
52             for (int i = 0; i < 32; i++)
53                 printf("%02x", pubkey.data[63-i]);
54             printf("\n");
55         }
56         else {
57             printf("secp256k1_ec_pubkey_create failed\n");
58         }
59 
60         // order N = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
61         unsigned int* pData = (unsigned int*)rand32;
62         pData[0] = bswap_32(0xFFFFFFFF);
63         pData[1] = bswap_32(0xFFFFFFFF);
64         pData[2] = bswap_32(0xFFFFFFFF);
65         pData[3] = bswap_32(0xFFFFFFFE);
66         pData[4] = bswap_32(0xBAAEDCE6);
67         pData[5] = bswap_32(0xAF48A03B);
68         pData[6] = bswap_32(0xBFD25E8C);
69         pData[7] = bswap_32(0xD0364140);
70         ret = secp256k1_ec_pubkey_create(pCtx, &pubkey, rand32);
71         if (ret) {
72             printf("private key\n0x");
73             for (int i = 0; i < 32; i++)
74                 printf("%02x", rand32[i]);
75             printf("\n");
76             printf("secp256k1_ec_pubkey_create success\n");
77             printf("0x");
78             for (int i = 0; i < 32; i++)
79                 printf("%02x", pubkey.data[31 - i]);
80             printf("\n0x");
81             for (int i = 0; i < 32; i++)
82                 printf("%02x", pubkey.data[63 - i]);
83             printf("\n");
84         }
85         else {
86             printf("secp256k1_ec_pubkey_create failed\n");
87         }
88 
89         secp256k1_context_destroy(pCtx);
90     }
91     
92     return 1;
93 }

secp256k1Test.c

程序第40，41行，以0x1为私钥产生公钥，即椭圆曲线生成元G。程序第62~70行，以阶n-1为私钥产生公钥，即(n-1)*G，这里仅为测试，所以两次取的私钥都是特殊值，正常情况下私钥要随机产生，程序最终运行结果如下

复制代码

this is for secp256k1 testing
secp256k1_context_randomize success
private key
0x0000000000000000000000000000000000000000000000000000000000000001
secp256k1_ec_pubkey_create success
0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
private key
0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364140
secp256k1_ec_pubkey_create success
0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
0xb7c52588d95c3b9aa25b0403f1eef75702e84bb7597aabe663b82f6f04ef2777

有椭圆曲线理论可知两次产生的公钥点互为逆元，它们关于x轴对称，x坐标相同，y坐标互为相反数（在有限域内y坐标之和为模数p)。

参考：

https://cloud.tencent.com/developer/news/586021

secp256k1算法详解一

1 简介

1.1 密码协议标准

1.2 有限域

1.3 有限域大小

1.4 Koblitz Curve

1.5 末位标记

2 源码及编译

2.1 Linux下编译

2.2 Windows编译

3 应用