前言

前段时间，我们处理了一则Java线程池配置不当导致的线上问题（参见好端端的线程池，怎么就卡死了？），本文将以此为案例，使用形式化语言，从数学角度进行证明。

形式化证明简介

首先需要搞清楚一个概念，形式化证明，也是通过编程的形式进行的，只不过这段代码使用形式化编程语言进行表达，从数理层面来看更为严谨，常见的形式化语言有：

Coq：广泛用于学术研究和软件形式化验证，历史悠久。
Lean4：最近在数学界引起了广泛关注，适合开发严格的数学证明。
Dafny：与C#和Java有相似的语法，适合编程语言内置规范。
ACSL：基于C语言的注释，适合进行语法和语义检查。
TLA+：用于建模算法和程序的形式语言，特别适合并发和分布式系统。

某些领域也有特定的工具，比如 Java Pathfinder (JPF) 用于Java程序的形式化验证，支持线程和并发的验证。

鉴于Lean4使用最为广泛，本次首先使用Lean4进行尝试。

Lean4 的安装

Lean4 可以在 vscode 中安装使用，也需要安装 Mathlib 数学库（类似于我们常用的三方依赖库）。本节将介绍其安装和使用方法。

Lean4 也有网页版 https://live.lean-lang.org/，但实测网站响应速度较差，推荐本地安装使用。

安装 vscode，我们使用这个 IDE 创建和运行 Lean 工程。
安装 Lean4 插件：打开 vscode 中的插件市场，搜索 Lean4，点击安装。

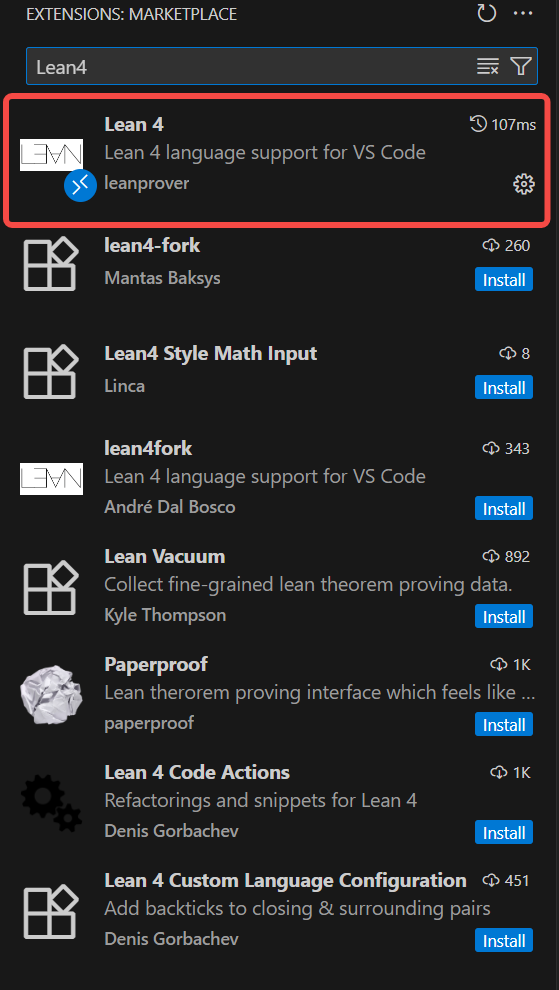
安装 elan：它是Lean4版本管理工具，类似于node里面的nvm。到官方网站 https://github.com/leanprover/elan?tab=readme-ov-file#elan-lean-version-manager 参考即可：

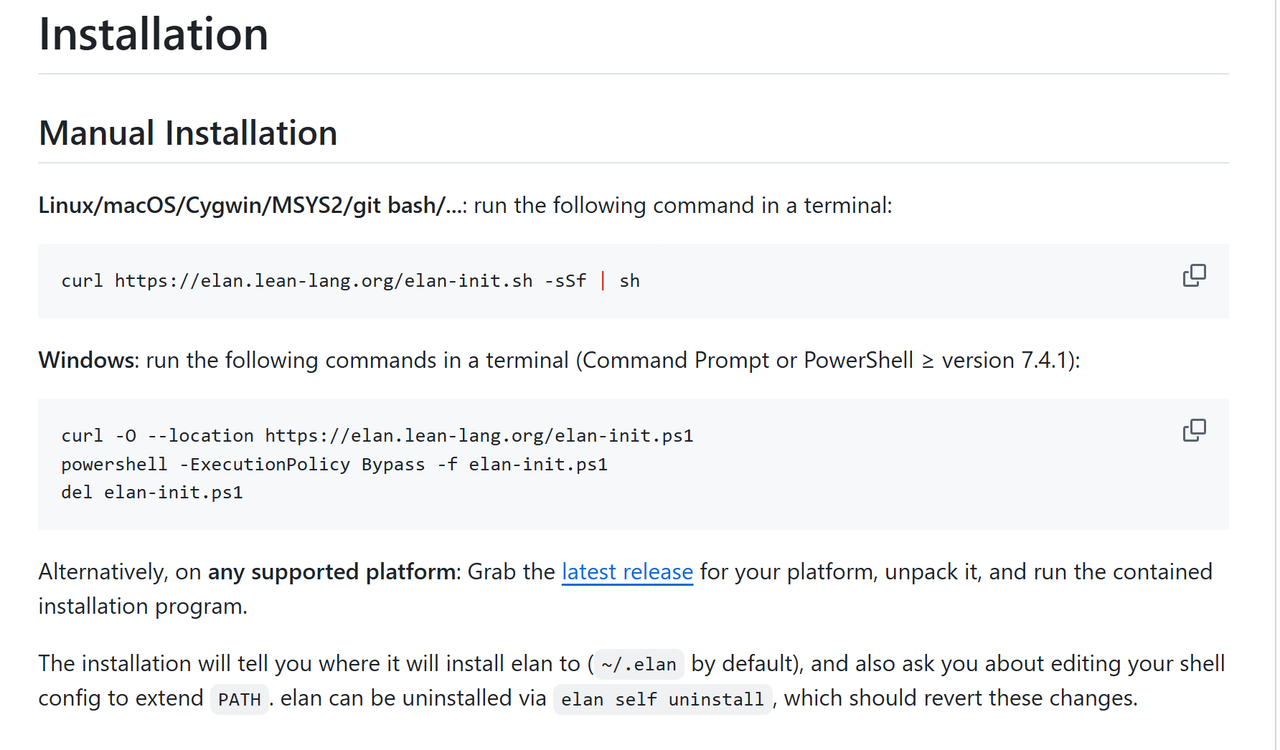
配置 mathlib：创建项目时使用 lean 的项目构建工具，指定 mathlib4，会自动安装 mathlib 依赖包：

lake +leanprover-community/mathlib4:lean-toolchain new <your_project_name> math

到这里，就可以开始编写 Lean 代码了（vscode会启动lean4服务器，允许即可）。

常用功能：

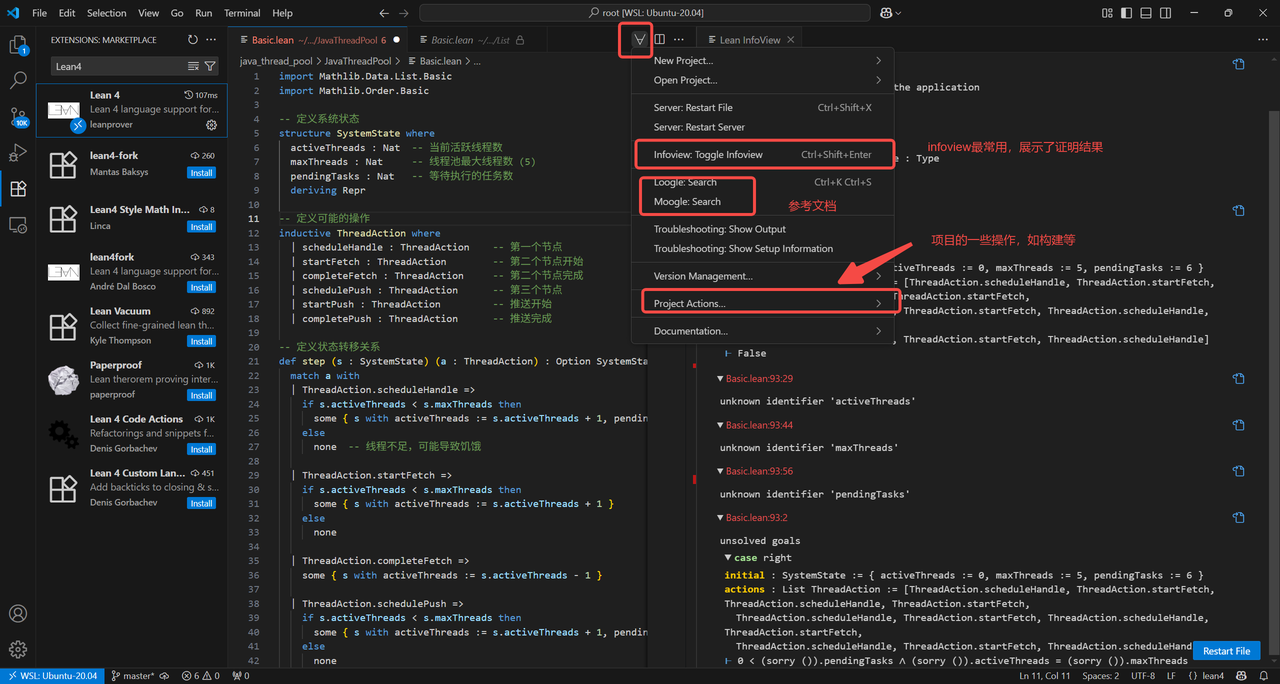
形式化证明

前面我们遇到的问题是：当任务数量大于线程池的核心线程数量后，由于任务间的依赖关系导致线程无法释放，最终导致新提交的任务被放到无界阻塞队列中，无法得到处理，最终系统处于假死状态。

为验证线程池资源是否存在资源耗尽的漏洞，可以参考如下Prompt（比较粗糙，作为示例已经够用了），让AI编写一段 Lean4 形式化代码：

复制代码

你是形式化证明专家，也是各种语言编程专家，尤其精通Java和Lean4。

我想用一段Lean4脚本验证：

配置场景：定义了一个线程池，其核心线程数为5、配置了无界阻塞队列、最大线程数为 Integer.MAX_VALUE（约21亿）

验证场景：当任务数量大于线程池的数量时，任务就会卡死，因为后续的节点已经没有线程可用了，对应的任务始终无法完成，因此已经被占用的线程无法释放（因为属于同一个任务）。此后继续提交的新任务会被放到无界阻塞队列中，表现出来就是系统处于假死状态。

请写一段Lean4程序。务必保持简洁。

为降低理解难度，做了一定程度的简化。

复制代码

import Mathlib.Data.Real.Basic

structure ThreadPool where
  corePoolSize : ℕ
  maxPoolSize : ℕ
  unboundedQueue : Bool := true  -- true 表示无界队列

def isDeadlocked (pool : ThreadPool) (tasks : ℕ) : Prop :=
  pool.corePoolSize < tasks ∧
  pool.unboundedQueue ∧
  pool.maxPoolSize >= pool.corePoolSize

theorem unbounded_queue_causes_deadlock :
  ∃ (pool : ThreadPool) (tasks : ℕ),
    pool.corePoolSize = 5 ∧
    pool.maxPoolSize = 2147483647 ∧
    pool.unboundedQueue = true ∧
    tasks > 5 ∧
    isDeadlocked pool tasks :=
by
  let pool : ThreadPool := { corePoolSize := 5, maxPoolSize := 2147483647, unboundedQueue := true }

          use pool, 6

          simp [isDeadlocked]

          constructor <;> trivial

解释一下：

1. import Mathlib.Data.Real.Basic：导入数学库（本例会使用实数定义，因此需要导入）;

2. structure定义线程池结构：

复制代码

structure ThreadPool where
  corePoolSize : ℕ
  maxPoolSize : ℕ
  unboundedQueue : Bool := true  -- true 表示无界队列

定义死锁条件（符号∧表示 "与"）:

def isDeadlocked (pool : ThreadPool) (tasks : ℕ) : Prop :=
pool.corePoolSize < tasks ∧
pool.unboundedQueue ∧
pool.maxPoolSize > pool.corePoolSize
声明定理和证明

先了解一下声明定理的语法，属于三段式结构：theorem name : Prop := proof：

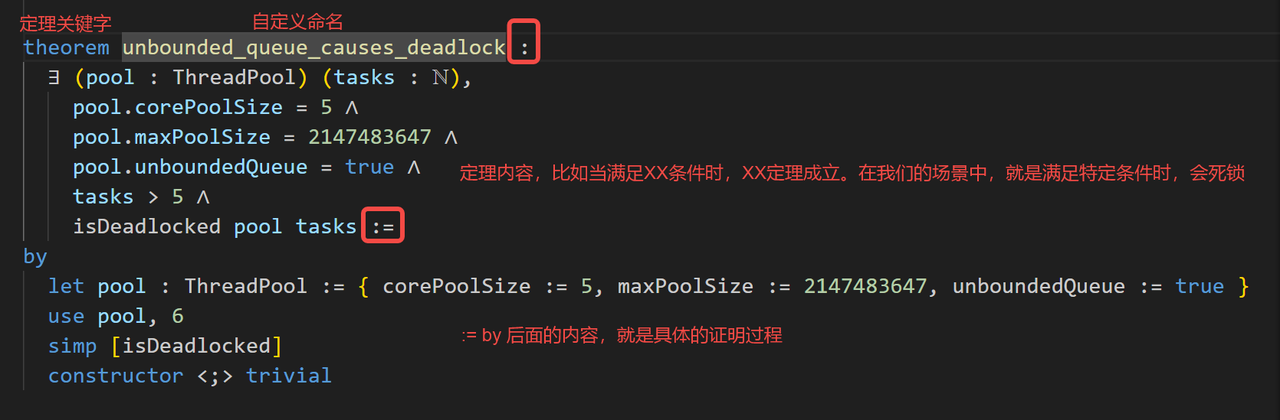
Prop 在我们的代码中对应：

复制代码

∃ (pool : ThreadPool) (tasks : ℕ),
    pool.corePoolSize = 5 ∧
    pool.maxPoolSize = 2147483647 ∧
    pool.unboundedQueue = true ∧
    tasks > 5 ∧
    isDeadlocked pool tasks

其中的符号∃表示存在性命题，翻译成人话就是：

复制代码

存在一个线程池 pool 和任务数 tasks，满足以下所有条件时，会导致死锁（isDeadlocked）：
1. 核心线程数 = 5
2. 最大线程数 = Integer.MAX_VALUE
3. 使用无界队列
4. 任务数 > 5

然后构造具体例子，证明命题成立。对应的代码：

复制代码

  let pool : ThreadPool := { corePoolSize := 5, maxPoolSize := 2147483647, unboundedQueue := true }
  use pool, 6

其中，let 定义具体线程池实例参数，use pool, 6提供例子（核心线程5时，提交6个任务），就可以准备证明了。

在随后的证明过程中，使用simp [isDeadlocked]把 isDeadlocked 的定义展开（类似于内联的概念），并自动把能计算出来的部分（比如 5 < 6）直接化简成 True，让证明变简单。

最后constructor <;> trivial的意思是：把目标拆成多个小条件（constructor），然后逐个（<;>）用"自动验证"（trivial，表示显然会成立的命题）解决。在我们的场景中：

目标是 5 < 6 ∧ true ∧ 2147483647 > 5。
constructor 将其拆成 3 个子目标：5 < 6、true、2147483647 > 5。
trivial 自动验证这些显然成立的子目标。

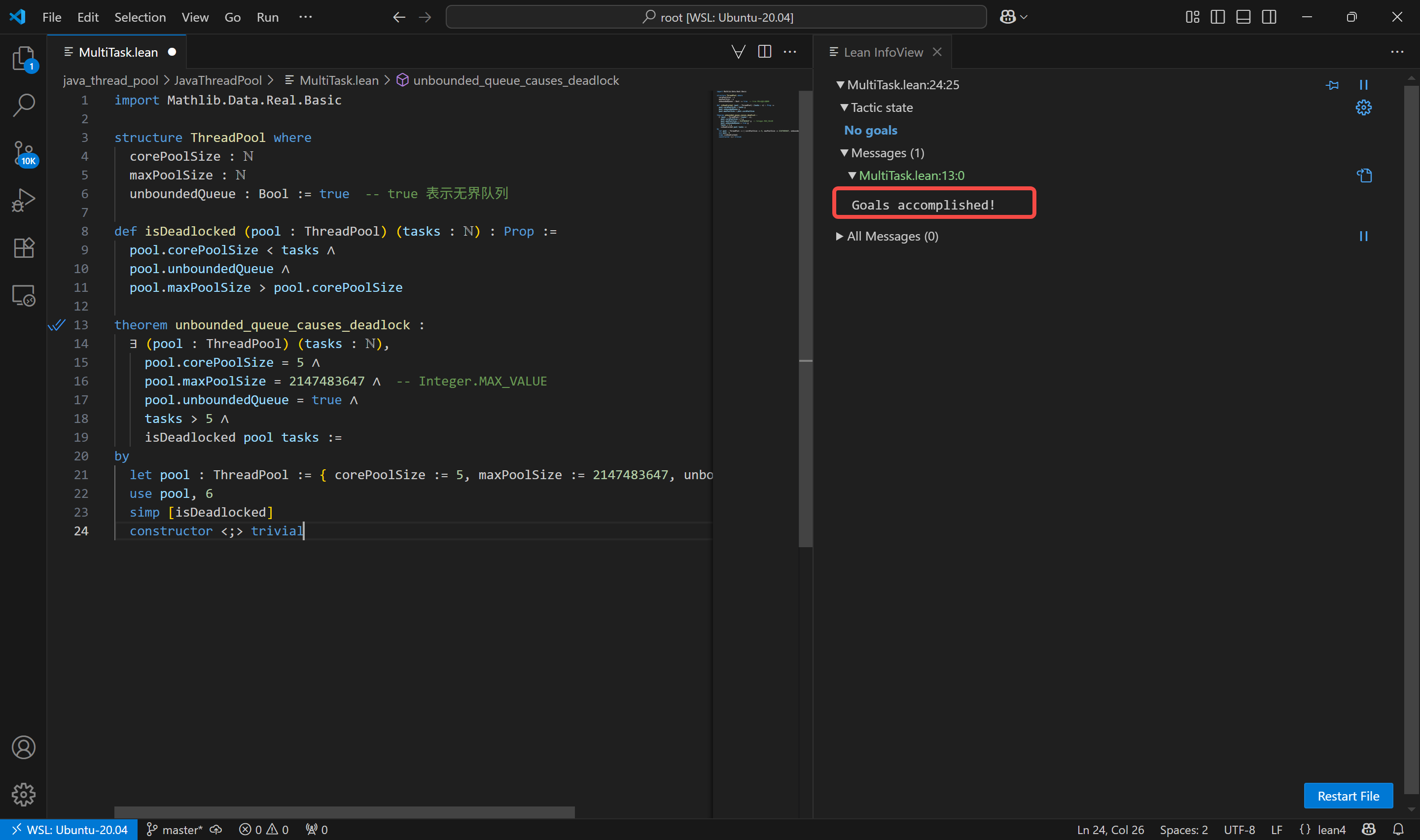
最终可以看到，我们定义的定理 unbounded_queue_causes_deadlock ，被成功地证明了：
Lean4 与 Rust

大家可能已经发现，Lean4 与 Rust 这两种编程语言的语法非常相似，其实不仅如此，他们的工具链也很相似：比如 Lean 的版本管理工具elan，类似于 Rust 的 rustup； Lean 的包管理器和构建工具lake ，类似于 Rust 的 cargo）。熟悉 Rust 的同学狂喜，哈哈。

后记

2025年，随着大模型能力的提升，多家模型引入了形式化证明，用来验证大模型解决数学问题的能力，比较常见的训练方法是提供一段形式化代码，并挖去某些内容（或本身就存在待证明的部分），让大模型进行补充，然后验证它补充的内容是否能使得形式化证明通过（参见 DeepSeek又在节前放大招！以及 DeepSeek-Prover-V2：让 AI 学会严谨证明）。这与我们的场景略有差异（我们是直接用大模型生成形式化验证代码，并且想办法用在工程领域）。

在当下的 AI 浪潮中，我们可以借助大模型的能力，在实践过程中不断学习 Lean4 语法，不断构建工程领域的各种"定理"库，并进行开放复用。随着这个库的不断丰富，我们对业务领域的抽象和构建能力也会有所提升。

需要说明的是，本文中的例子非常简单，大家可以作为入门材料参考。在实际的应用中，若要验证某个领域的执行逻辑是否符合预期（如状态机中的状态变化），需要精确理解领域含义和各种动作条件，才能做出明确的抽象，这个过程是比较费力的。不过恰恰在这个过程中，我们能够有机会从具体的业务实现中抽离出来，更为严谨地描述系统行为（从这个角度看，形式化证明与单元测试、集成测试等概念有相似之处）。

另外，单纯靠 AI 写形式化代码会很痛苦，因为很难确认写出来的形式化代码是否正确，导致需要反复修改。因此，有必要熟悉特定形式化语言的语法和编写规范，就好比使用 AI 生成业务代码，需要具备一定的 Java/GoLang 等语言功底。

说了这么多，好像还没提到形式化语言在工程领域的特定落地场景（因为还没完全想清楚）。先别急，我会继续探索 TLA+、Dafny、Coq 等形式化编程语言，看看哪种更适合软件领域的工程化落地，边实践边想。

若有探索形式化方法应用落地的同学，欢迎交流。

学习资源

一些 Lean4 学习资源，包括一些博客文章，以及官方的参考手册。

使用Lean4进行形式化建模（以Java线程池为例）

前言

形式化证明简介

Lean4 的安装

形式化证明

后记

学习资源