Trie 字典树的原理和应用解析

Ofnoname2025-07-04 1:02

如何高效地存储和查找大量字符串或前缀？比如自动补全、拼写检查、敏感词过滤等场景，都对字符串的处理速度有很高要求。哈希表虽然查找快，但并不擅长前缀匹配；普通树结构虽然灵活，但对于大量字符串的处理效率并不理想。

这时候，Trie（发音类似"try"，又称前缀树、字典树）作为一种专为字符串检索优化的数据结构，成为了解决这类问题的利器。它不仅能高效完成字符串的插入、查找、前缀搜索，还能拓展到处理整数、支持合并等高级应用。

什么是 Trie 树？

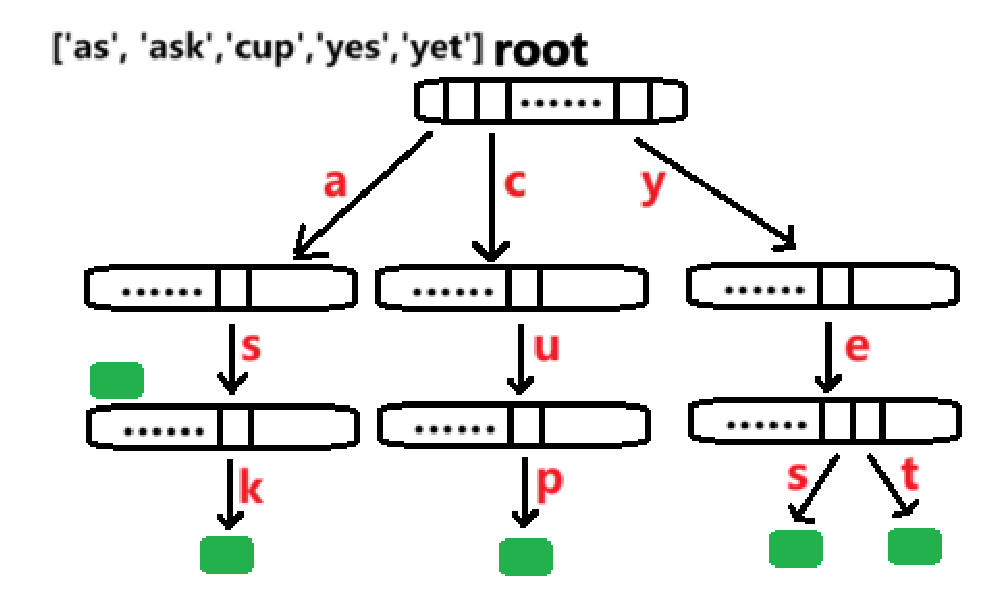
Trie 树（前缀树、字典树）是一种多叉树结构，主要用于高效地存储和检索字符串集合，尤其擅长处理前缀相关的查询问题。每个节点通常表示一个字符，根节点为空。树中的每一条从根到叶子的路径，都对应一个字符串。

Trie 的结构特点

  • 每个节点代表一个字符：但节点本身不保存字符串，只记录字符和子节点。
  • 从根节点到某一节点的路径，拼接起来即为某个字符串的前缀。
  • 单词的结束可以用布尔标记或计数来表示 ：通常会用一个布尔变量isEnd或count等来表示以当前节点结尾的字符串数量。

在实际生产中， Trie 的在自动补全、拼写检查与纠错、敏感词检测与过滤、前缀计数、单词统计和处理与二进制相关的高效查询（如最大异或值）中都有应用

Trie 树的 C++ 实现

假定仅使用 a-z 字符集。Trie 树主要有三种常用操作：插入（Insert）、查询（Search）和前缀判断（StartsWith），有些场景下还需要删除（Delete）和合并（Merge）等高级操作。其核心思想是将每个字符串按字符拆分，逐层存储在多叉树中。

  • 插入操作：从根节点开始，依次遍历字符串的每个字符。如果对应字符的子节点不存在，则新建节点。插入结束后，将最后一个字符节点标记为"单词结尾"。
  • 查询操作：同样从根节点出发，依次按字符查找子节点，若全部存在且最后一个节点是"单词结尾"，则表示单词存在。
  • 前缀查询：与查找类似，但只要能走到最后一个字符即可，不必判断是否为"单词结尾"。
  • 删除操作：需要回溯删除冗余节点，但实际场景中较少使用。
  • 合并操作：将两个 Trie 树合并为一个，常用于多源数据的合并处理。

节点结构设计

cpp 复制代码 
struct TrieNode {
    TrieNode* children[26];  // 指向26个字母的子节点
    bool isEnd;              // 是否为一个单词的结尾

    TrieNode() : isEnd(false) {
        for (int i = 0; i < 26; ++i) children[i] = nullptr;
    }
};

Trie 类的基本操作

cpp 复制代码 
class Trie {
private:
    TrieNode* root;

public:
    Trie() {
        root = new TrieNode();
    }

    // 插入单词
    void insert(const std::string& word) {
        TrieNode* node = root;
        for (char ch : word) {
            int idx = ch - 'a';
            if (!node->children[idx])
                node->children[idx] = new TrieNode();
            node = node->children[idx];
        }
        node->isEnd = true;
    }

    // 查找完整单词
    bool search(const std::string& word) {
        TrieNode* node = root;
        for (char ch : word) {
            int idx = ch - 'a';
            if (!node->children[idx])
                return false;
            node = node->children[idx];
        }
        return node->isEnd;
    }

    // 判断是否有某个前缀
    bool startsWith(const std::string& prefix) {
        TrieNode* node = root;
        for (char ch : prefix) {
            int idx = ch - 'a';
            if (!node->children[idx])
                return false;
            node = node->children[idx];
        }
        return true;
    }

    // 删除单词（可选，简化版）
    bool remove(const std::string& word) {
        return remove(root, word, 0);
    }

private:
    // 递归删除单词辅助函数
    bool remove(TrieNode* node, const std::string& word, int depth) {
        if (!node) return false;
        if (depth == word.size()) {
            if (!node->isEnd) return false;
            node->isEnd = false;
            return isEmpty(node); // 是否可以安全删除该节点
        }
        int idx = word[depth] - 'a';
        if (remove(node->children[idx], word, depth + 1)) {
            delete node->children[idx];
            node->children[idx] = nullptr;
            return !node->isEnd && isEmpty(node);
        }
        return false;
    }

    // 判断节点是否没有任何子节点
    bool isEmpty(TrieNode* node) {
        for (int i = 0; i < 26; ++i)
            if (node->children[i]) return false;
        return true;
    }
};

Trie 树的合并

在某些应用中，我们可能需要将两个 Trie 树合并。可以使用递归合并两个节点。

cpp 复制代码 
// 将 src 的内容合并到 dest 上
void mergeTrie(TrieNode* dest, TrieNode* src) {
    if (!src) return;
    if (src->isEnd) dest->isEnd = true;
    for (int i = 0; i < 26; ++i) {
        if (src->children[i]) {
            if (!dest->children[i])
                dest->children[i] = new TrieNode();
            mergeTrie(dest->children[i], src->children[i]);
        }
    }
}

mergeTrie(trie1.root, trie2.root);

复杂度分析

在限定一个较小字符集的情况下，字典树的复杂度是线性的：

  • 插入、查询、前缀判断的时间复杂度均为 \(O(L)\)，L 为字符串长度，与集合规模无关。
  • 空间复杂度最坏为 O(N \* L) ，N为单词数，L为平均长度。

当然可以！下面是**Trie 树在整数上的应用（01-Trie）**这一部分的详细讲解：

01-Trie 树处理整数

Trie 不仅可以用于字符串处理，其思想同样可以用来高效处理整数序列，尤其是涉及二进制位运算的问题。这里常见的做法是将每个整数按二进制位拆解，从高位到低位依次插入到 Trie 树中，这种结构被称为01-Trie（或二进制 Trie）。

01-Trie 的原理

假定我们要处理一些 32 位无符号整数，可以认为：将其二进制表示（一个32位长的01字符串）视为一个字符串存储

  • 节点含义：每个节点有两个子节点，分别代表 0 和 1 两种可能（即当前二进制位是 0 还是 1）。
  • 存储过程：将每个整数拆为固定长度（如 32 位）的二进制序列，从最高位（31）到最低位（0）插入（特殊情况下也可能从低到高）。
  • 查找过程：与字符串 Trie 类似，通过遍历对应的二进制位进行路径选择。

典型应用：最大异或对

给定一个整数数组，找出数组中任意两个数的最大异或值。

核心思路：

  • 对每个数，将其二进制形式插入到 Trie 树；
  • 查询时，希望每一位都取与当前位相反的分支，以获取更大的异或值；
  • 对每个数分别查询并更新最大异或结果。
cpp 复制代码 
struct TrieNode {
    TrieNode* children[2];
    TrieNode() { children[0] = children[1] = nullptr; }
};

class Trie01 {
private:
    TrieNode* root;
public:
    Trie01() { root = new TrieNode(); }

    // 插入一个数的二进制表示
    void insert(int num) {
        TrieNode* node = root;
        for (int i = 31; i >= 0; --i) {  // 以32位为例
            int bit = (num >> i) & 1;
            if (!node->children[bit])
                node->children[bit] = new TrieNode();
            node = node->children[bit];
        }
    }

    // 查询与num异或结果最大的数
    int query(int num) {
        TrieNode* node = root;
        int res = 0;
        for (int i = 31; i >= 0; --i) {
            int bit = (num >> i) & 1;
            int desired = bit ^ 1; // 希望找相反的位
            if (node->children[desired]) {
                res |= (1 << i);
                node = node->children[desired];
            } else {
                node = node->children[bit];
            }
        }
        return res;
    }
};

01-Trie 分支固定为2（0/1）。用于二进制位、最大异或、区间问题、计数相关的问题。可以在节点中记录通过该节点的数字个数，实现删除、计数等高级操作。对于负数，可以通过补码直接处理。

好的，下面是Trie 树如何处理大字符集这一部分的详细讲解：

Trie 树如何处理大字符集

在前面的实现中，我们使用的是仅包含 26 个小写字母的 Trie。此时，每个节点只需维护 26 个指针（children 数组），空间和查询效率都很可控。但如果字符集变大，比如：

  • 包含大小写英文字母（A-Z, a-z）：52
  • 包含所有 ASCII 可见字符：128
  • 支持 Unicode 或中日韩字符：几千甚至几万

那么，Trie 的空间复杂度会随字符集大小 \(C\) 线性增长。

  • 每个节点需要 \(O(C)\) 的空间。
  • 假设有 \(N\) 个字符串，每个字符串长度为 L，则最坏空间复杂度为 O(N \* L \* C) 。

在超大字符集下，Trie 的空间浪费会非常明显。即使实际数据量远小于全部可能字符，仍然需要为每个节点预留完整的 children 数组。

优化 Trie 的常用方法

1. 动态结构替代定长数组

  • unordered_map<char, TrieNode*> 或 map<char, TrieNode*>

    用哈希表或平衡树来动态存储存在的子节点，只为出现过的字符分配空间，极大降低空间浪费。

    cpp 复制代码 
    struct TrieNode {
    unordered_map<char, TrieNode*> children;
    bool isEnd = false;
};

  • 对于字符集非常稀疏或不连续的情况，这种方式尤其有效。

2. 压缩 Trie（又称字典树压缩，Radix Tree/Patricia Trie）

当我们用压缩 Trie（又称 Radix Tree 或 Patricia Trie）时，Trie 节点不再仅仅保存单个字符，而是保存一段字符串。其基本思想是：

  • 在 Trie 中遇到只有一个子节点的"链路"时，可以将这段连续的字符合并成一个节点，节点保存字符串片段（比如 "abc"），而不是一个字符。
  • 只有遇到分叉（即出现多个分支）时才拆分。

结构变更如下：

cpp 复制代码 
struct RadixNode {
    string label;  // 当前节点代表的字符串片段
    unordered_map<char, RadixNode*> children;
    bool isEnd = false;
};

插入和查找时，需要在每一步将目标字符串与节点的 label 进行最长公共前缀匹配，然后再判断是完全匹配、部分匹配还是完全不匹配。若部分匹配，则需要将当前节点分裂成两部分。

这能有效减少链式节点和极度稀疏节点，节省空间。查询时实际访问节点数大幅减少，提升长串的处理效率。

复制代码 
(root)
 ├── "ap"
 │    ├── "ple" (isEnd)
 │    └── "ricot" (isEnd)
 └── "bee" (isEnd)

压缩 Trie 特别适用于存储大量有公共前缀的长字符串数据，可以让 Trie 在空间与速度上都更高效。

3. 混合使用

  • 小字符集用定长数组（查询速度快）。
  • 大字符集用哈希表或平衡树（整体略慢于定长数组，但可节省大量空间。）。
热门推荐
01Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code02全球最强模型Grok4，国内已可免费使用！（附教程）03vue数据变化但页面不变04KGG转MP3工具|非KGM文件|解密音频05sqli-labs 靶场 less-8、9、10 第八关到第十关详解：布尔注入，时间注入06扣子开源本地部署教程 丨Coze智能体小白喂饭级指南07干翻 Typora！MilkUp：完全免费的桌面端 Markdown 编辑器！08【2025.7.18】更新vscode后所有.vue文件template标签后报红的临时解决办法，Vue - Official 插件3.0.2导致09ChatGPT Agent 完全使用指南：2025年7月最新功能详解10《魔兽世界》提示lua警告的含义及解决方法