Matrix - 技术栈

概述

Matrix 是一个用于处理 2D 图形变换的工具类，它持有一个 3X3 的矩阵，用于对坐标进行转换。

其结构如下：

MSCALE_X, MSKEW_X, MTRANS_X

MSKEW_Y, MSCALE_Y, MTRANS_Y

MPERSP_0,MPERSP_1, MPERSP_2

其中 SCALE 表示缩放，SKEW 表示斜切（旋转时会影响这个），TRANS 表示平移，PERSP 代表透视。

原理

看下面的代码，假定有一个点，点坐标为（500f，500f），将这个点绕着坐标原点顺时针旋转 30° 后，新的坐标点是多少？

kotlin 复制代码

class MyView @JvmOverloads constructor(
    context: Context,
    attributeSet: AttributeSet? = null,
    defStyleAttr: Int = 0): View(context, attributeSet, defStyleAttr) {
    companion object{
        private val TAG = MyView::class.java.simpleName
    }
    // 初始坐标为（500f，500f）
    private val point = floatArrayOf(500f, 500f)
    // matrix 初始化
    private val matrix = Matrix()
    private val path = Path()

    init {
        // 将 matrix 绕着（0，0）旋转 30°
        matrix.setRotate(30f)
    }

    private val paint = Paint().apply {
        isAntiAlias = true
        color = context.getColor(android.R.color.black)
        style = Paint.Style.STROKE
        strokeWidth = 2f
    }

    private val textPaint = Paint().apply {
        color = context.getColor(android.R.color.holo_red_light)
        isAntiAlias = true
        style = Paint.Style.STROKE
        textSize = 30f
        strokeWidth = 2f
    }

    override fun onDraw(canvas: Canvas) {
        super.onDraw(canvas)
        // 画一条从（0，0）到（500f，500f）的线段
        path.lineTo(point[0], point[1])
        canvas.drawPath(path, paint)
        canvas.drawText("(${point[0]}, ${point[1]})", point[0], point[1], textPaint)
        
        // 将 matrix 应用到点坐标上
        matrix.mapPoints(point)
        path.moveTo(0f, 0f)
        // 画一条从（0，0）到变换后的坐标的线段
        path.lineTo(point[0], point[1])
        canvas.drawPath(path, paint)
        
        canvas.drawText("(${point[0]}, ${point[1]})", point[0], point[1], textPaint)
    }
}

运行后显示如下：

可以看到通过将旋转 30° 后的 matrix 作用于点上，可以拿到这个点绕着坐标原点旋转 30° 后的新的坐标点。

假定有一个坐标点 P1(x1, y1)，其与 x 轴的夹角为 α，其与坐标原点的距离为 r，则有：

ini 复制代码

x1 = r * cosα
y1 = r * sinα

现在把 P1 绕着坐标原点顺时针旋转 θ 度，旋转之后的坐标点为 P2（x2, y2），则有：

arduino 复制代码

x2 = r * cos(α + θ) = r * cosα * cosθ - r * sinα * sinθ = x1 * cosθ - y1 * sinθ
y2 = r * sin(α + θ) = r * sinα * cosθ + r * cosα * sinθ = y1 * cosθ + x1 * sinθ

换成矩阵运算如下所示：

css 复制代码

[x2]   [cosθ -sinθ 0 ]     [x1]   
[y2] = [sinθ cosθ  0 ]  *  [y1] 
[1 ]   [0    0     1 ]     [1 ]

可以在 init 代码块中通过下面的代码打印 matrix 旋转 30° 后的值：

kotlin 复制代码

init {
    matrix.setRotate(30f)
    val floatArray = FloatArray(9)
    matrix.getValues(floatArray)
    val sb = StringBuilder()
    floatArray.forEachIndexed{ index, item ->
        sb.append(item)
        if(index != floatArray.size -1){
            sb.append(", ")
        }
    }
    Log.d(TAG, sb.toString())
}

打印如下：

复制代码

0.8660254, -0.5, 0.0, 0.5, 0.8660254, 0.0, 0.0, 0.0, 1.0

可以看到刚好跟前面的矩阵：

csharp 复制代码

[cos30 -sin30 0 ]     
[sin30 cos30  0 ]  
[0     0      1 ]

里面的值一一对应。

对一个图形做旋转操作会影响与它对应的 Matrix 的左上角的四个值，对一个图形做平移操作则会影响 MTRANS_X 和 MTRANS_Y，如果把 Z 轴也加进来，则会影响 MPERSP_0、MPERSP_1、MPERSP_2，如果只是在 X 轴和 Y 轴上进行移动、旋转和缩放，那么这 3 个值可以不用管。

基本方法解析

构造函数

scss 复制代码

Matrix()
Matrix(Matrix src)

Matrix 类的构造函数有两个，一个是直接创建一个单位矩阵，第二个是根据 src 创建一个 src 的拷贝（采用 deep copy）。

什么是单位矩阵？

单位矩阵主对角线(从左上到右下)上的元素都是 1 ，其他位置的元素都是 0，上面使用空参的构造函数构造出来的矩阵就是一个单位矩阵。

isIdentity 与 isAffine

scss 复制代码

isIdentity()  // 判断是否是单位矩阵
isAffine()    // 判断是否是仿射矩阵

什么是仿射矩阵？

仿射矩阵会保留 2D 图形的"平直性"（变换后直线还是直线，圆弧还是圆弧），和"平行性"（指保持 2D 图形的的相对位置关系不变，平行线还是平行线，而且直线上的点的比例关系不变），仿射矩阵可以通过一系列的原子变换的复合来实现，原子变换包括：平移、缩放、翻转、旋转和斜切。这里除了透视可以改变 Z 轴以外，其他的变换基本都是上述的原子变换，所以，只要最后一行是 0,0,1 就是仿射矩阵。

rectStaysRect

java 复制代码

boolean rectStaysRect()  // 判断该矩阵是否将一个矩形映射为另一个矩形

如果该 matrix 是单位矩阵，只有平移和缩放，或旋转的角度是 90 度的倍数时，该方法返回 true。

reset

scss 复制代码

reset()  // 重置矩阵为单位矩阵

setTranslate

arduino 复制代码

setTranslate(float dx, float dy) // matrix 平移

setScale

java 复制代码

public void setScale(float sx, float sy, float px, float py)
public void setScale(float sx, float sy)  // matrix 缩放

sx，sy 是缩放的倍数，px, py 是缩放的中心。

setRotate

arduino 复制代码

setRotate(float degrees, float px, float py) 
setRotate(float degrees)   // matrix 旋转

degrees 是旋转的角度，px, py 是旋转的中心。

setSinCos

arduino 复制代码

setSinCos(float sinValue, float cosValue, float px, float py)
setSinCos(float sinValue, float cosValue)

将 matrix 按照指定的 sine 和 cosine 值旋转，px, py 是旋转的中心点，其实跟上面的 setRotate() 方法是一个作用，只不过这里的参数是 sine 和 cosine 值。

setSkew

arduino 复制代码

setSkew(float kx, float ky, float px, float py)
setSkew(float kx, float ky)   // matrix 错切

kx，ky 是错切因子，px，py 是错切的中心。

postXXX

除了上面的 setXXX() 方法之外， Matrix 还提供了对应的复合操作的方法，比如有一个 Canvas，你先对其进行旋转，然后缩放，最后平移，这时候就需要使用复合操作的方法，先调用 postRotate()，然后调用 postScale()，最后调用 postTranslate()。如果你最后调用的是 setTranslate() 就是错误的，因为 setXXX() 方法会把前面对 Matrix 的修改都清空，最终只有 setXXX() 会起作用。

preXXX

除了 postXXX() ，Matrix 还提供了 preXXX() 方法，preXXX() 称为前乘，postXXX() 称为后乘。

arduino 复制代码

preScale(float sx, float sy)  // M' = M * S(sx, sy)
postScale(float sx, float sy)  // M' = S(sx, sy) * M

看下面的代码：

ini 复制代码

Matrix matrix = new Matrix();
matrix.setTranslate(100, 1000);
matrix.preScale(0.5f, 0.5f);

这里是前乘，换算成数学式如下：

如果是后乘，换算成数学式如下：

可以看到两者的结果并不一样。

注意矩阵乘法的顺序与变换的顺序是相反的，比如先缩放（S），后平移（T），对应的矩阵乘法是：M = T × S。

invert

java 复制代码

boolean invert(Matrix inverse)  // 反转矩阵

如果该矩阵不为空，且能反转，就返回 true 并将反转后的结果写入inverse；否则返回 false 。当前矩阵 * inverse = 单位矩阵。

mapPoints

css 复制代码

mapPoints(float[] pts)  
mapPoints(float[] dst, float[] src)
mapPoints(float[] dst, int dstIndex, float[] src, int srcIndex,
        int pointCount)

将 matrix 应用于 2D 点坐标，会将变换后的点坐标写回到 pts 数组中，注意 pts 数组是这样的： $x0, y0, x1, y1, ...$ 。

mapVectors

css 复制代码

mapVectors(float[] vecs)
mapVectors(float[] dst, float[] src) 
mapVectors(float[] dst, int dstIndex, float[] src, int srcIndex, int vectorCount)

与上面的 mapPoints() 方法基本类似，这里是将矩阵作用于向量，由于向量的平移前后是相等的，所以这个方法不会对平移相关的方法产生反应，如果只是调用了平移相关的方法，那么得到的值和原本的一致。

实战

实现一个自定义 View，将该 View 使用 Matrix 进行变换，然后在该 View 上绘制矩形，矩形以手指落下的点为左上角，手指移动的点为右下角，且该矩形需要平行于变换后的 View。

kotlin 复制代码

class TransformedRectView(context: Context, attrs: AttributeSet?) : View(context, attrs) {

    private val paint = Paint(Paint.ANTI_ALIAS_FLAG).apply {
        color = Color.RED
        style = Paint.Style.STROKE
        strokeWidth = 5f
    }

    private val axisPaint = Paint().apply {
        color = Color.BLUE
        strokeWidth = 3f
    }

    private var downPoint = PointF()
    private var movePoint = PointF()

    private val transformMatrix = Matrix() // 假设这是你应用到 Canvas 的变换矩阵
    private val inverseMatrix = Matrix()

    private val rectF = RectF()

    init {
        // 旋转 30 度，缩放 0.5 倍，平移 (200f, 200f)
        transformMatrix.postRotate(30f)
        transformMatrix.postScale(0.5f, 0.5f)
        transformMatrix.postTranslate(200f, 200f)
    }

    override fun onTouchEvent(event: MotionEvent): Boolean {
        when (event.action) {
            MotionEvent.ACTION_DOWN -> {
                // 起点
                downPoint = PointF(event.x, event.y)

            }
            MotionEvent.ACTION_MOVE -> {
                // 终点
                movePoint = PointF(event.x, event.y)
                invalidate()
            }
        }
        return true
    }

    override fun onDraw(canvas: Canvas) {
        super.onDraw(canvas)

        // 应用变换矩阵（前乘）
        canvas.concat(transformMatrix)

        // 绘制变换后的坐标系辅助线
        drawCanvasAxes(canvas)

        // 绘制变换对齐的矩形
        if ((downPoint.x != movePoint.x) and (downPoint.y != movePoint.y)) {
            val p1 = floatArrayOf(downPoint.x, downPoint.y)
            val p2 = floatArrayOf(movePoint.x, movePoint.y)

            // 将屏幕坐标转为变换前 Canvas 坐标
            transformMatrix.invert(inverseMatrix)
            inverseMatrix.mapPoints(p1)
            inverseMatrix.mapPoints(p2)

            rectF.set(min(p1[0], p2[0]),
                min(p1[1], p2[1]),
                max(p1[0], p2[0]),
                max(p1[1], p2[1]))
            // 因为 canvas 已经被 transformMatrix 变换了，所以画出来的是变换后的效果   
            canvas.drawRect(rectF, paint)  
        }
    }

    private fun drawCanvasAxes(canvas: Canvas) {
        canvas.drawLine(0f, 0f, 2000f, 0f, axisPaint) // X轴
        canvas.drawLine(0f, 0f, 0f, 800f, axisPaint) // Y轴
    }
}

使用手指在屏幕上拖动后显示如下：

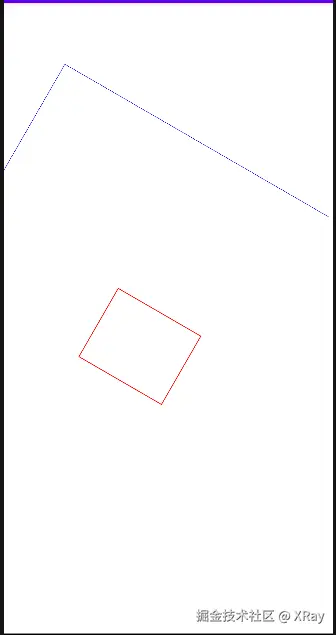
这样就成功地在经过 Matrxi 变换后的 View 上绘制出了平行于变换后的 View 的矩形。