本文基于UC Berkeley研究团队的最新论文Reinforcement Learning with Action Chunking (arXiv:2507.07969)撰写,旨在为读者提供Q-Chunking技术的深入解读。如有技术问题或讨论,欢迎通过私信交流。
一、引言
在强化学习领域,长期稀疏奖励任务一直是一个棘手的挑战。想象一下教机器人学会做饭:从拿起食材到最终完成一道菜,中间可能需要数百个动作步骤,但只有在最后品尝时才能获得奖励反馈。传统的强化学习方法在这种场景下往往表现不佳,因为智能体需要通过大量的随机探索才能偶然发现正确的动作序列。
最近,来自UC Berkeley的研究团队提出了一种名为Q-Chunking的新方法[1],为这一问题提供了一个优雅的解决方案。Q-Chunking的核心思想是将强化学习从单个动作级别提升到动作序列(action chunks)级别,通过利用离线数据中的时间相干行为模式来指导在线探索。
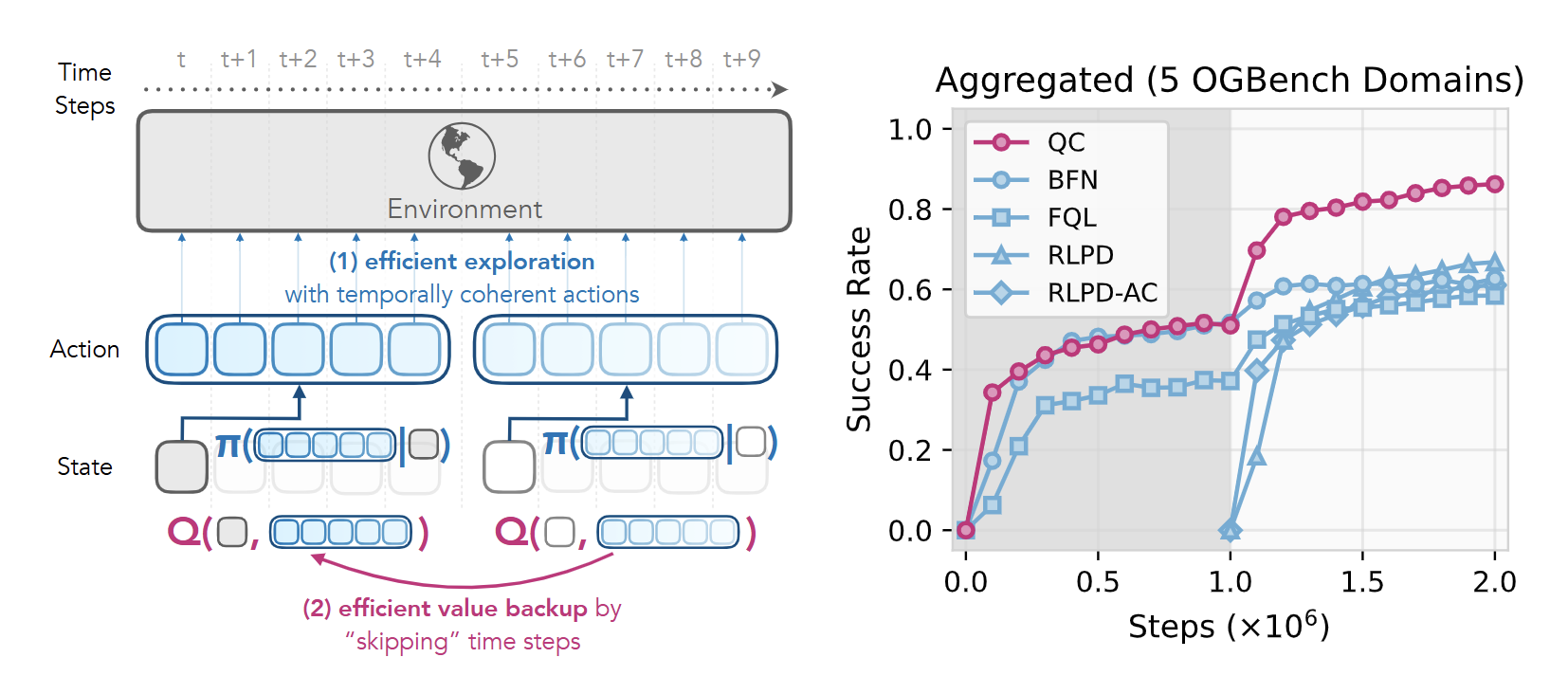
本文将深入解析Q-Chunking的技术原理,重点阐述其核心概念、数学公式、具体实现方法以及算法伪代码,帮助读者全面理解这一创新方法的技术细节。
二、问题背景与动机
传统强化学习的探索困境
传统的强化学习算法通常采用单步决策模式:在每个时间步 t t t,智能体观察当前状态 s t s_t st,选择一个动作 a t a_t at,执行后获得奖励 r t r_t rt并转移到下一个状态 s t + 1 s_{t+1} st+1。这种逐步决策的方式在短期任务中表现良好,但在长期稀疏奖励任务中面临严重挑战。
问题的根源在于探索的随机性。当智能体需要执行一系列连贯的动作才能获得奖励时,纯随机的动作选择几乎不可能偶然发现正确的动作序列。例如,在机器人操作任务中,"抓取-移动-放置"这样的动作序列需要高度的时间一致性,单个动作的随机扰动可能导致整个任务失败。
动作分块的启发
动作分块(Action Chunking)的概念最初在模仿学习领域得到广泛应用。与传统的单步动作预测不同,动作分块方法让策略一次性预测并执行一个动作序列。这种方法的优势在于能够捕获动作之间的时间依赖关系,生成更加连贯和有效的行为模式。
在离线数据中,我们经常能观察到具有时间一致性的动作模式。这些模式可能来自专家演示、脚本化策略或人类操作员的行为。这些时间相干的动作序列本质上代表了解决特定子任务的"技能"或"原语"。如果能够有效利用这些模式,就可以显著提升强化学习的探索效率。
Q-Chunking的核心洞察
Q-Chunking方法的关键洞察是:可以将时间差分(TD)强化学习扩展到动作序列级别,同时通过行为约束确保学习的策略不会偏离离线数据分布太远。
具体而言,Q-Chunking包含两个核心设计原则:
-
时间扩展动作空间上的Q-learning :不再在单个动作上进行Q-learning,而是在长度为 h h h的动作序列上进行学习。
-
扩展动作空间中的行为约束:在动作序列级别施加约束,确保学习的策略能够利用离线数据中的时间相干模式。
这种设计带来了两个重要优势:首先,策略可以通过时间相干的动作进行优化,使其行为更接近离线数据中的有效模式;其次,critic能够执行有效的n-step备份,在没有离策略偏差的情况下加速价值传播。
三、Q-Chunking的技术原理
时间扩展的策略和价值函数
Q-Chunking的第一个核心创新是将传统的单步策略和价值函数扩展到时间维度。
传统方法的数学表示:
在标准强化学习中,我们定义:
- 策略: π ( a t ∣ s t ) \pi(a_t|s_t) π(at∣st) - 给定状态 s t s_t st,输出单个动作 a t a_t at的概率分布
- Q函数: Q ( s t , a t ) Q(s_t, a_t) Q(st,at) - 评估在状态 s t s_t st执行动作 a t a_t at的长期价值
Q-Chunking方法的数学表示:
Q-Chunking将这些概念扩展到动作序列:
- 策略: π ϕ ( a t : t + h ∣ s t ) = π ϕ ( a t , a t + 1 , ... , a t + h − 1 ∣ s t ) \pi_\phi(a_{t:t+h}|s_t) = \pi_\phi(a_t, a_{t+1}, \ldots, a_{t+h-1}|s_t) πϕ(at:t+h∣st)=πϕ(at,at+1,...,at+h−1∣st) - 给定状态 s t s_t st,输出长度为 h h h的动作序列
- Q函数: Q θ ( s t , a t : t + h ) = Q θ ( s t , a t , a t + 1 , ... , a t + h − 1 ) Q_\theta(s_t, a_{t:t+h}) = Q_\theta(s_t, a_t, a_{t+1}, \ldots, a_{t+h-1}) Qθ(st,at:t+h)=Qθ(st,at,at+1,...,at+h−1) - 评估在状态 s t s_t st执行动作序列 a t : t + h a_{t:t+h} at:t+h的长期价值
符号说明:
- a t : t + h a_{t:t+h} at:t+h表示从时间步 t t t开始的 h h h个连续动作,即 [ a t , a t + 1 , ... , a t + h − 1 ] [a_t, a_{t+1}, \ldots, a_{t+h-1}] [at,at+1,...,at+h−1]
- ϕ \phi ϕ和 θ \theta θ分别表示策略网络和价值网络的参数
- h h h是动作序列的长度,也称为"chunk size"
这种扩展的关键在于,Q函数现在评估的不是单个动作的价值,而是整个动作序列的价值,这使得算法能够捕获动作之间的时间依赖关系。
时间差分学习的重新设计
为了更好地理解Q-Chunking的创新之处,我们需要对比传统TD学习和Q-Chunking的TD学习机制。
传统1-step TD学习
标准的时间差分学习使用以下更新规则:
Q ( s t , a t ) ← r t + γ Q ( s t + 1 , a t + 1 ) (1) Q(s_t, a_t) \leftarrow r_t + \gamma Q(s_{t+1}, a_{t+1}) \tag{1} Q(st,at)←rt+γQ(st+1,at+1)(1)
其中:
- r t r_t rt是在时间步 t t t获得的即时奖励
- γ ∈ [ 0 , 1 ] \gamma \in [0,1] γ∈[0,1]是折扣因子,用于平衡即时奖励和未来奖励的重要性
- a t + 1 a_{t+1} at+1是在状态 s t + 1 s_{t+1} st+1下根据当前策略选择的动作
对应的TD损失函数为:
L ( θ ) = E ( s t , a t , r t , s t + 1 ) ∼ D [ ( Q θ ( s t , a t ) − ( r t + γ Q θ ˉ ( s t + 1 , a t + 1 ) ) ) 2 ] (2) L(\theta) = \mathbb{E}{(s_t,a_t,r_t,s{t+1}) \sim \mathcal{D}} \left[ \left( Q_\theta(s_t, a_t) - \left( r_t + \gamma Q_{\bar{\theta}}(s_{t+1}, a_{t+1}) \right) \right)^2 \right] \tag{2} L(θ)=E(st,at,rt,st+1)∼D[(Qθ(st,at)−(rt+γQθˉ(st+1,at+1)))2](2)
公式解释:
- E ( s t , a t , r t , s t + 1 ) ∼ D \mathbb{E}{(s_t,a_t,r_t,s{t+1}) \sim \mathcal{D}} E(st,at,rt,st+1)∼D表示对数据集 D \mathcal{D} D中的转移样本求期望
- Q θ ˉ Q_{\bar{\theta}} Qθˉ表示目标网络,其参数 θ ˉ \bar{\theta} θˉ是 θ \theta θ的延迟更新版本,用于稳定训练
- 损失函数衡量当前Q值估计与TD目标之间的差异
这种方法每次更新只能将价值信息向后传播一个时间步,在长期任务中收敛速度较慢。
n-step返回方法
为了加速价值传播,研究者提出了n-step返回方法:
Q ( s t , a t ) ← ∑ i = 0 n − 1 γ i r t + i + γ n Q ( s t + n , a t + n ) (3) Q(s_t, a_t) \leftarrow \sum_{i=0}^{n-1} \gamma^i r_{t+i} + \gamma^n Q(s_{t+n}, a_{t+n}) \tag{3} Q(st,at)←i=0∑n−1γirt+i+γnQ(st+n,at+n)(3)
公式解释:
- ∑ i = 0 n − 1 γ i r t + i \sum_{i=0}^{n-1} \gamma^i r_{t+i} ∑i=0n−1γirt+i是从时间步 t t t开始的 n n n步累积折扣奖励
- γ n Q ( s t + n , a t + n ) \gamma^n Q(s_{t+n}, a_{t+n}) γnQ(st+n,at+n)是 n n n步后的价值估计
- 这种方法能够将价值信息向后传播 n n n个时间步,显著加速学习过程
然而,当 n n n-step轨迹中的动作不是由当前策略生成时(即存在离策略数据),这种方法会引入偏差,影响学习稳定性。具体来说,如果轨迹中的动作 a t + 1 , ... , a t + n − 1 a_{t+1}, \ldots, a_{t+n-1} at+1,...,at+n−1是由不同的策略生成的,那么价值估计就不再准确。
Q-Chunking的TD学习
Q-Chunking提出了一种新的TD更新机制:
Q ( s t , a t : t + h ) ← ∑ i = 0 h − 1 γ i r t + i + γ h Q ( s t + h , a t + h : t + 2 h ) (4) Q(s_t, a_{t:t+h}) \leftarrow \sum_{i=0}^{h-1} \gamma^i r_{t+i} + \gamma^h Q(s_{t+h}, a_{t+h:t+2h}) \tag{4} Q(st,at:t+h)←i=0∑h−1γirt+i+γhQ(st+h,at+h:t+2h)(4)
对应的TD损失函数为:
L ( θ ) = E s t , a t : t + h , { r t + i } i = 0 h − 1 , s t + h [ ( Q θ ( s t , a t : t + h ) − ∑ i = 0 h − 1 γ i r t + i − γ h Q θ ˉ ( s t + h , a t + h : t + 2 h ) ) 2 ] (5) L(\theta) = \mathbb{E}{s_t, a{t:t+h}, \{r_{t+i}\}{i=0}^{h-1}, s{t+h}} \left[ \left( Q_\theta(s_t, a_{t:t+h}) - \sum_{i=0}^{h-1} \gamma^i r_{t+i} - \gamma^h Q_{\bar{\theta}}(s_{t+h}, a_{t+h:t+2h}) \right)^2 \right] \tag{5} L(θ)=Est,at:t+h,{rt+i}i=0h−1,st+h⎣⎡(Qθ(st,at:t+h)−i=0∑h−1γirt+i−γhQθˉ(st+h,at+h:t+2h))2⎦⎤(5)
其中 a t + h : t + 2 h ∼ π ϕ ( ⋅ ∣ s t + h ) a_{t+h:t+2h} \sim \pi_\phi(\cdot|s_{t+h}) at+h:t+2h∼πϕ(⋅∣st+h)是在状态 s t + h s_{t+h} st+h下由当前策略生成的下一个动作序列。
公式解释:
- Q θ ( s t , a t : t + h ) Q_\theta(s_t, a_{t:t+h}) Qθ(st,at:t+h)评估在状态 s t s_t st执行动作序列 a t : t + h a_{t:t+h} at:t+h的价值
- ∑ i = 0 h − 1 γ i r t + i \sum_{i=0}^{h-1} \gamma^i r_{t+i} ∑i=0h−1γirt+i是执行动作序列期间获得的累积折扣奖励
- γ h Q θ ˉ ( s t + h , a t + h : t + 2 h ) \gamma^h Q_{\bar{\theta}}(s_{t+h}, a_{t+h:t+2h}) γhQθˉ(st+h,at+h:t+2h)是 h h h步后的价值估计,其中下一个动作序列由当前策略生成
- 这确保了目标值的计算是同策略的(on-policy),避免了异策略(off-policy)偏差
三种方法的关键差异
| 方法 | 价值传播距离 | 异策略偏差 | 学习稳定性 | 数学表达式 |
|---|---|---|---|---|
| 1-step TD | 1个时间步 | 无 | 高但收敛慢 | r t + γ Q ( s t + 1 , a t + 1 ) r_t + \gamma Q(s_{t+1}, a_{t+1}) rt+γQ(st+1,at+1) |
| n-step返回 | n个时间步 | 有(当存在异策略数据时) | 中等 | ∑ i = 0 n − 1 γ i r t + i + γ n Q ( s t + n , a t + n ) \sum_{i=0}^{n-1} \gamma^i r_{t+i} + \gamma^n Q(s_{t+n}, a_{t+n}) ∑i=0n−1γirt+i+γnQ(st+n,at+n) |
| Q-Chunking | h个时间步 | 无 | 高且收敛快 | ∑ i = 0 h − 1 γ i r t + i + γ h Q ( s t + h , a t + h : t + 2 h ) \sum_{i=0}^{h-1} \gamma^i r_{t+i} + \gamma^h Q(s_{t+h}, a_{t+h:t+2h}) ∑i=0h−1γirt+i+γhQ(st+h,at+h:t+2h) |
Q-Chunking的优势在于:它既能实现快速的价值传播(类似n-step方法),又能避免异策略偏差(因为目标值中的动作序列是由当前策略生成的),从而在保持学习稳定性的同时加速收敛。
行为约束机制
Q-Chunking的第二个核心创新是在动作序列级别引入行为约束。这一机制的目的是确保学习的策略能够有效利用离线数据中的时间相干模式,同时避免在在线学习过程中偏离有效的行为分布。
约束优化问题的数学表述
Q-Chunking将策略学习表述为一个约束优化问题:
max π ϕ E s t ∼ ρ , a t : t + h ∼ π ϕ ( ⋅ ∣ s t ) [ Q θ ( s t , a t : t + h ) ] (6) \max_{\pi_\phi} \mathbb{E}{s_t \sim \rho, a{t:t+h} \sim \pi_\phi(\cdot|s_t)} \left[ Q_\theta(s_t, a_{t:t+h}) \right] \tag{6} πϕmaxEst∼ρ,at:t+h∼πϕ(⋅∣st)[Qθ(st,at:t+h)](6)
subject to: D ^ ( π ϕ ( a t : t + h ∣ s t ) , π D ( a t : t + h ∣ s t ) ) ≤ ε \text{subject to: } \hat{D}(\pi_\phi(a_{t:t+h}|s_t), \pi_D(a_{t:t+h}|s_t)) \leq \varepsilon subject to: D^(πϕ(at:t+h∣st),πD(at:t+h∣st))≤ε
公式解释:
- ρ \rho ρ是状态分布,通常来自离线数据或在线经验
- π D ( a t : t + h ∣ s t ) \pi_D(a_{t:t+h}|s_t) πD(at:t+h∣st)表示离线数据 D \mathcal{D} D中观察到的行为分布
- D ^ ( ⋅ , ⋅ ) \hat{D}(\cdot, \cdot) D^(⋅,⋅)是某种距离度量函数,用于衡量学习策略与离线行为分布的差异
- ε ≥ 0 \varepsilon \geq 0 ε≥0是约束强度参数,控制允许的偏差程度
这个约束优化问题的直观含义是:我们希望学习的策略在最大化Q值的同时,不能偏离离线数据中观察到的行为模式太远。
行为约束的重要性
在动作序列级别施加约束特别重要,原因如下:
单步约束的局限性:如果只在单个动作级别施加约束:
D ^ ( π ϕ ( a t ∣ s t ) , π D ( a t ∣ s t ) ) ≤ ε \hat{D}(\pi_\phi(a_t|s_t), \pi_D(a_t|s_t)) \leq \varepsilon D^(πϕ(at∣st),πD(at∣st))≤ε
策略可能会生成在局部看起来合理但在全局缺乏一致性的动作序列。例如,每个单独的动作都可能出现在离线数据中,但它们的组合可能从未被观察过,导致无效的行为。
序列级约束的优势:在动作序列级别施加约束:
D ^ ( π ϕ ( a t : t + h ∣ s t ) , π D ( a t : t + h ∣ s t ) ) ≤ ε \hat{D}(\pi_\phi(a_{t:t+h}|s_t), \pi_D(a_{t:t+h}|s_t)) \leq \varepsilon D^(πϕ(at:t+h∣st),πD(at:t+h∣st))≤ε
能够保持动作之间的时间依赖关系,确保生成的行为具有与离线数据相似的时间一致性。这种一致性对于复杂的操作任务尤其重要,因为这些任务通常需要精确的动作协调。
约束机制的优势
这种约束机制带来几个重要优势:
-
利用先验知识:离线数据中的动作序列通常包含有效的子任务解决方案,约束机制确保这些知识得到充分利用。
-
结构化探索:与随机探索相比,基于离线模式的探索更加结构化和高效。数学上,这相当于在策略空间中定义了一个有效的搜索区域。
-
避免灾难性遗忘:在在线微调过程中,约束机制防止策略完全偏离已知的有效行为。
两种实现方案
基于不同的距离度量和约束实现方式,Q-Chunking提出了两种具体的实现方案:QC(使用隐式KL约束)和QC-FQL(使用显式Wasserstein约束)。接下来我们将详细介绍这两种方案的技术细节。
四、QC方法:基于隐式KL约束的实现
Best-of-N采样机制
QC方法采用一种巧妙的隐式约束实现方式,通过Best-of-N采样来平衡Q值最大化和行为约束。
算法流程的数学描述
QC方法的动作选择过程可以数学化地描述为以下步骤:
步骤1:行为策略训练
首先使用流匹配(Flow Matching)或其他生成模型训练一个行为克隆策略 f x ( ⋅ ∣ s ) f_x(\cdot|s) fx(⋅∣s),使其近似离线数据中的行为分布:
f x ≈ π D f_x \approx \pi_D fx≈πD
步骤2:候选动作生成
在每个决策时刻,从行为策略中采样 N N N个候选动作序列:
{ a 1 , a 2 , ... , a N } ∼ f x ( ⋅ ∣ s t ) (7) \{a^1, a^2, \ldots, a^N\} \sim f_x(\cdot|s_t) \tag{7} {a1,a2,...,aN}∼fx(⋅∣st)(7)
步骤3:最优动作选择
从 N N N个候选中选择Q值最高的动作序列:
a ∗ ← arg max a i ∈ { a 1 , a 2 , ... , a N } Q θ ( s t , a i ) (8) a^* \leftarrow \arg\max_{a^i \in \{a^1, a^2, \ldots, a^N\}} Q_\theta(s_t, a^i) \tag{8} a∗←argai∈{a1,a2,...,aN}maxQθ(st,ai)(8)
理论保证:KL散度上界
Best-of-N采样方法具有重要的理论保证。根据先前的研究[2],这种采样方式能够提供KL散度的闭式上界:
D K L ( a ∗ ∥ f x ( ⋅ ∣ s ) ) ≤ log N − N − 1 N (9) D_{KL}(a^* \| f_x(\cdot|s)) \leq \log N - \frac{N-1}{N} \tag{9} DKL(a∗∥fx(⋅∣s))≤logN−NN−1(9)
公式解释:
- D K L ( a ∗ ∥ f x ( ⋅ ∣ s ) ) D_{KL}(a^* \| f_x(\cdot|s)) DKL(a∗∥fx(⋅∣s))是选择的最优动作序列 a ∗ a^* a∗与行为策略 f x f_x fx之间的KL散度
- 右侧是一个关于采样数量 N N N的函数,当 N → ∞ N \to \infty N→∞时,上界趋近于 log N \log N logN
- 当 N = 1 N=1 N=1时,上界为0,意味着完全遵循行为策略
- 当 N N N增大时,上界增大,允许更多的偏离
这个不等式的重要意义在于,通过调整采样数量 N N N,我们可以精确控制学习策略与行为策略之间的KL散度:
- 较小的 N N N:约束较紧,策略更接近离线行为,探索较少
- 较大的 N N N:约束较松,策略有更大的探索空间,但计算成本增加
TD损失函数的完整形式
QC方法的完整TD损失函数为:
KaTeX parse error: Undefined control sequence: \substack at position 25: ... = \mathbb{E}{\̲s̲u̲b̲s̲t̲a̲c̲k̲{s_t, a{t:t+h}...
其中:
- s t , a t : t + h s_t, a_{t:t+h} st,at:t+h来自离线数据集 D \mathcal{D} D或在线经验回放缓冲区
- a t + h : t + 2 h a_{t+h:t+2h} at+h:t+2h通过Best-of-N采样从 f x ( ⋅ ∣ s t + h ) f_x(\cdot|s_{t+h}) fx(⋅∣st+h)中选择:
a t + h : t + 2 h = arg max a i ∈ { a 1 , ... , a N } Q θ ˉ ( s t + h , a i ) a_{t+h:t+2h} = \arg\max_{a^i \in \{a^1, \ldots, a^N\}} Q_{\bar{\theta}}(s_{t+h}, a^i) at+h:t+2h=argai∈{a1,...,aN}maxQθˉ(st+h,ai) - θ ˉ \bar{\theta} θˉ是目标网络参数,用于稳定训练
实现优势
QC方法的主要优势包括:
-
实现简单 :只需要训练两个网络组件(行为策略 f x f_x fx和Q函数 Q θ Q_\theta Qθ),无需复杂的约束优化算法。
-
计算效率 :Best-of-N采样的计算复杂度为 O ( N ) O(N) O(N),当 N N N不太大时开销可控。
-
理论保证:公式(9)提供的KL散度上界给出了明确的理论基础,便于分析和调试。
-
参数可控 :通过调整 N N N值可以直观地控制探索与利用的平衡,具有良好的可解释性。
五、QC-FQL方法:基于显式Wasserstein约束的实现
Wasserstein距离约束
QC-FQL方法采用更直接的约束实现方式,使用2-Wasserstein距离来度量策略分布与行为分布之间的差异:
W 2 ( π ϕ , f x ( ⋅ ∣ s ) ) ≤ ε (11) W_2(\pi_\phi, f_x(\cdot|s)) \leq \varepsilon \tag{11} W2(πϕ,fx(⋅∣s))≤ε(11)
公式解释:
- W 2 ( ⋅ , ⋅ ) W_2(\cdot, \cdot) W2(⋅,⋅)是2-Wasserstein距离(也称为Earth Mover's Distance)
- 相比KL散度,Wasserstein距离在处理分布差异时具有更好的几何性质和数值稳定性
- Wasserstein距离考虑了概率分布的几何结构,对于连续动作空间特别适用
2-Wasserstein距离的数学定义为:
W 2 ( μ , ν ) = inf γ ∈ Π ( μ , ν ) ( ∫ ∥ x − y ∥ 2 d γ ( x , y ) ) 1 / 2 W_2(\mu, \nu) = \inf_{\gamma \in \Pi(\mu, \nu)} \left( \int \|x - y\|^2 d\gamma(x, y) \right)^{1/2} W2(μ,ν)=γ∈Π(μ,ν)inf(∫∥x−y∥2dγ(x,y))1/2
其中 Π ( μ , ν ) \Pi(\mu, \nu) Π(μ,ν)是边际分布为 μ \mu μ和 ν \nu ν的所有联合分布的集合。
噪声条件策略参数化
QC-FQL使用一种特殊的策略参数化方式:
π ϕ ( a t : t + h ∣ s t ) = μ ϕ ( s t , z ) , 其中 z ∼ N ( 0 , I ⋅ α h ) (12) \pi_\phi(a_{t:t+h}|s_t) = \mu_\phi(s_t, z), \quad \text{其中} \quad z \sim \mathcal{N}(0, I \cdot \alpha_h) \tag{12} πϕ(at:t+h∣st)=μϕ(st,z),其中z∼N(0,I⋅αh)(12)
参数说明:
- μ ϕ ( s , z ) : S × R A ⋅ h → R A ⋅ h \mu_\phi(s, z) : \mathcal{S} \times \mathbb{R}^{A \cdot h} \rightarrow \mathbb{R}^{A \cdot h} μϕ(s,z):S×RA⋅h→RA⋅h是一个噪声条件的动作预测模型
- z z z是从多元高斯分布采样的噪声向量,维度为 A ⋅ h A \cdot h A⋅h( A A A是单个动作的维度)
- α h > 0 \alpha_h > 0 αh>0是与动作序列长度相关的方差参数
- I I I是单位矩阵
这种参数化的优势是能够通过单次前向传递直接生成动作序列:
a t : t + h = μ ϕ ( s t , z ) , z ∼ N ( 0 , I ⋅ α h ) a_{t:t+h} = \mu_\phi(s_t, z), \quad z \sim \mathcal{N}(0, I \cdot \alpha_h) at:t+h=μϕ(st,z),z∼N(0,I⋅αh)
避免了Best-of-N采样的计算开销。
联合优化目标
QC-FQL的训练目标结合了Q值最大化和行为约束,通过以下损失函数实现:
L ( ϕ ) = E s t ∼ D , z ∼ N ( 0 , I ⋅ α h ) [ α ∥ z 1 − μ ϕ ( s t , z 1 ) ∥ 2 − Q θ ( s t , μ ϕ ( s t , z 1 ) ) ] (13) L(\phi) = \mathbb{E}{s_t \sim \mathcal{D}, z \sim \mathcal{N}(0, I \cdot \alpha_h)} \left[ \alpha \|z^1 - \mu\phi(s_t, z^1)\|^2 - Q_\theta(s_t, \mu_\phi(s_t, z^1)) \right] \tag{13} L(ϕ)=Est∼D,z∼N(0,I⋅αh)[α∥z1−μϕ(st,z1)∥2−Qθ(st,μϕ(st,z1))](13)
公式解释 :
这个损失函数包含两个关键部分:
-
蒸馏项(Distillation Term) :
α ∥ z 1 − μ ϕ ( s t , z 1 ) ∥ 2 \alpha \|z^1 - \mu_\phi(s_t, z^1)\|^2 α∥z1−μϕ(st,z1)∥2- 确保策略输出接近行为克隆策略的输出
- z 1 z^1 z1是从单位高斯分布采样的噪声
- 参数 α > 0 \alpha > 0 α>0控制蒸馏强度
-
Q值最大化项 :
− Q θ ( s t , μ ϕ ( s t , z 1 ) ) -Q_\theta(s_t, \mu_\phi(s_t, z^1)) −Qθ(st,μϕ(st,z1))- 鼓励策略生成高Q值的动作序列
- 负号表示我们要最大化Q值(等价于最小化负Q值)
参数 α \alpha α控制两个目标之间的平衡:
- 较大的 α \alpha α:策略更接近离线行为,约束更紧
- 较小的 α \alpha α:允许更多的探索,约束更松
理论分析:Wasserstein约束的上界
可以证明,损失函数(13)提供了Wasserstein约束的上界。具体地,有以下不等式成立:
L ( ϕ ) ≥ E s t ∼ D , z ∼ N ( 0 , I ⋅ α h ) [ α W 2 ( π ϕ ( ⋅ ∣ s t ) , f x ( ⋅ ∣ s t ) ) 2 − Q θ ( s t , μ ϕ ( s t , z 1 ) ) ] (14) L(\phi) \geq \mathbb{E}{s_t \sim \mathcal{D}, z \sim \mathcal{N}(0, I \cdot \alpha_h)} \left[ \alpha W_2(\pi\phi(\cdot|s_t), f_x(\cdot|s_t))^2 - Q_\theta(s_t, \mu_\phi(s_t, z^1)) \right] \tag{14} L(ϕ)≥Est∼D,z∼N(0,I⋅αh)[αW2(πϕ(⋅∣st),fx(⋅∣st))2−Qθ(st,μϕ(st,z1))](14)
证明思路 :
这个不等式基于以下观察:当策略 μ ϕ \mu_\phi μϕ通过噪声条件参数化时,蒸馏项 ∥ z 1 − μ ϕ ( s t , z 1 ) ∥ 2 \|z^1 - \mu_\phi(s_t, z^1)\|^2 ∥z1−μϕ(st,z1)∥2提供了Wasserstein距离的一个上界估计。
这意味着优化损失函数 L ( ϕ ) L(\phi) L(ϕ)能够隐式地满足Wasserstein约束(11)。
TD损失函数
QC-FQL的Q函数训练使用以下TD损失:
KaTeX parse error: Undefined control sequence: \substack at position 25: ... = \mathbb{E}{\̲s̲u̲b̲s̲t̲a̲c̲k̲{s_t, a{t:t+h}...
与QC方法的区别:
- QC方法:目标值中的下一个动作序列通过Best-of-N采样选择
- QC-FQL方法:目标值直接使用策略网络 μ ϕ \mu_\phi μϕ生成的动作序列,无需额外的采样过程
这使得QC-FQL在推理时具有 O ( 1 ) O(1) O(1)的计算复杂度,而QC方法需要 O ( N ) O(N) O(N)的复杂度。
方法对比
| 特性 | QC方法 | QC-FQL方法 |
|---|---|---|
| 约束类型 | 隐式KL约束: D K L ≤ log N − N − 1 N D_{KL} \leq \log N - \frac{N-1}{N} DKL≤logN−NN−1 | 显式Wasserstein约束: W 2 ≤ ε W_2 \leq \varepsilon W2≤ε |
| 动作选择 | Best-of-N采样: arg max a i Q ( s , a i ) \arg\max_{a^i} Q(s, a^i) argmaxaiQ(s,ai) | 直接网络输出: μ ϕ ( s , z ) \mu_\phi(s, z) μϕ(s,z) |
| 计算复杂度 | O ( N ) O(N) O(N)(需要评估 N N N个候选) | O ( 1 ) O(1) O(1)(单次前向传递) |
| 理论保证 | KL散度闭式上界 | Wasserstein距离上界 |
| 参数调节 | 采样数量 N N N | 平衡参数 α \alpha α |
| 数值稳定性 | 依赖于 N N N的选择 | 通常更稳定 |
实现考虑
优势:
- 计算效率:推理时只需一次前向传递,适合实时应用
- 数值稳定性:Wasserstein距离的几何性质提供更好的数值稳定性
- 连续优化 :参数 α \alpha α可以连续调节,提供更细粒度的控制
挑战:
- 超参数调节 :需要仔细调节 α \alpha α和 α h \alpha_h αh参数
- 理论复杂性:Wasserstein约束的理论分析相对复杂
- 实现复杂度:需要实现噪声条件网络和相应的训练过程
两种方法各有优势:QC方法实现简单且理论清晰,适合对约束有精确要求的场景;QC-FQL方法计算效率更高,适合需要快速推理的实时应用。
六、算法伪代码
为了帮助读者更好地理解Q-Chunking的具体实现,我们提供两种方法的详细算法伪代码。
Algorithm 1: QC算法
python
def QC_algorithm(D, h, N, gamma, num_offline_epochs, num_online_steps):
"""
QC算法实现
参数:
- D: 离线数据集
- h: 动作序列长度 (chunk size)
- N: Best-of-N采样数量
- gamma: 折扣因子
- num_offline_epochs: 离线训练轮数
- num_online_steps: 在线训练步数
"""
# 初始化网络
f_x = BehaviorPolicy() # 行为策略网络
Q_theta = QNetwork() # Q函数网络
Q_theta_target = copy.deepcopy(Q_theta) # 目标网络
# ==================== 离线预训练阶段 ====================
for epoch in range(num_offline_epochs):
# 训练行为克隆策略
# 目标: f_x ≈ π_D (近似离线数据中的行为分布)
for batch in DataLoader(D):
s_t, a_t_to_th = batch
# 流匹配或其他生成模型损失
behavior_loss = flow_matching_loss(f_x, s_t, a_t_to_th)
update_network(f_x, behavior_loss)
# 训练Q函数
for batch in DataLoader(D):
s_t, a_t_to_th, rewards, s_th = batch
# 为目标值生成下一个动作序列 (Best-of-N采样)
candidates = []
for _ in range(N):
candidate = f_x.sample(s_th) # 从行为策略采样
candidates.append(candidate)
# 选择Q值最高的候选: a* = argmax Q(s_{t+h}, a^i)
q_values = [Q_theta_target(s_th, cand) for cand in candidates]
best_idx = argmax(q_values)
a_th_to_t2h = candidates[best_idx]
# 计算TD目标: Σ γ^i r_{t+i} + γ^h Q(s_{t+h}, a_{t+h:t+2h})
cumulative_reward = sum(gamma**i * rewards[i] for i in range(h))
td_target = cumulative_reward + gamma**h * Q_theta_target(s_th, a_th_to_t2h)
# Q函数损失: L(θ) = [Q_θ(s_t, a_{t:t+h}) - target]²
q_pred = Q_theta(s_t, a_t_to_th)
q_loss = (q_pred - td_target.detach())**2
update_network(Q_theta, q_loss)
# 软更新目标网络: θ̄ ← τθ + (1-τ)θ̄
soft_update(Q_theta_target, Q_theta, tau=0.005)
# ==================== 在线微调阶段 ====================
current_state = env.reset()
action_chunk = None
step_in_chunk = 0
for step in range(num_online_steps):
# 每h步选择新的动作序列
if step % h == 0:
# Best-of-N采样选择动作序列
candidates = []
for _ in range(N):
candidate = f_x.sample(current_state)
candidates.append(candidate)
# 选择Q值最高的候选
q_values = [Q_theta(current_state, cand) for cand in candidates]
best_idx = argmax(q_values)
action_chunk = candidates[best_idx]
step_in_chunk = 0
# 执行当前动作
action = action_chunk[step_in_chunk]
next_state, reward, done = env.step(action)
# 存储经验到回放缓冲区
replay_buffer.add(current_state, action, reward, next_state, done)
# 更新网络(如果有足够的经验)
if len(replay_buffer) > batch_size:
# 从回放缓冲区采样并更新网络
# (类似离线训练过程)
update_networks_with_replay_data()
current_state = next_state
step_in_chunk += 1
if done:
current_state = env.reset()
action_chunk = None
step_in_chunk = 0
def best_of_n_sampling(f_x, state, N, Q_theta):
"""
Best-of-N采样实现
理论保证: D_KL(a* || f_x(·|s)) ≤ log N - (N-1)/N
"""
candidates = []
q_values = []
for _ in range(N):
# 从行为策略采样候选动作序列
action_chunk = f_x.sample(state)
candidates.append(action_chunk)
# 计算Q值
q_value = Q_theta(state, action_chunk)
q_values.append(q_value)
# 选择Q值最高的候选
best_idx = argmax(q_values)
return candidates[best_idx]Algorithm 2: QC-FQL算法
python
def QC_FQL_algorithm(D, h, alpha, alpha_h, gamma, num_offline_epochs, num_online_steps):
"""
QC-FQL算法实现
参数:
- D: 离线数据集
- h: 动作序列长度
- alpha: 约束强度参数
- alpha_h: 噪声方差参数
- gamma: 折扣因子
"""
# 初始化网络
f_x = FlowMatchingPolicy() # 流匹配行为策略
mu_phi = NoiseConditionedPolicy() # 噪声条件策略网络
Q_theta = QNetwork() # Q函数网络
Q_theta_target = copy.deepcopy(Q_theta)
action_dim = env.action_space.shape[0]
# ==================== 离线预训练阶段 ====================
for epoch in range(num_offline_epochs):
# 训练流匹配行为策略
for batch in DataLoader(D):
s_t, a_t_to_th = batch
flow_loss = flow_matching_loss(f_x, s_t, a_t_to_th)
update_network(f_x, flow_loss)
# 联合训练策略和Q函数
for batch in DataLoader(D):
s_t, a_t_to_th, rewards, s_th = batch
batch_size = s_t.shape[0]
# ========== 训练策略网络 μ_φ ==========
# 采样噪声: z ~ N(0, I·α_h)
z = sample_noise(shape=(batch_size, action_dim * h),
variance_scale=alpha_h)
# 策略预测: a = μ_φ(s_t, z)
predicted_actions = mu_phi(s_t, z)
# 策略损失: L(φ) = α||z¹ - μ_φ(s_t, z¹)||² - Q_θ(s_t, μ_φ(s_t, z¹))
distillation_loss = alpha * torch.norm(z - predicted_actions, dim=1)**2
q_loss = -Q_theta(s_t, predicted_actions)
policy_loss = (distillation_loss + q_loss).mean()
update_network(mu_phi, policy_loss)
# ========== 训练Q函数 ==========
# 为目标值生成下一个动作序列
z_target = sample_noise(shape=(batch_size, action_dim * h),
variance_scale=alpha_h)
next_actions = mu_phi(s_th, z_target)
# TD目标: Σ γ^i r_{t+i} + γ^h Q(s_{t+h}, μ_φ(s_{t+h}, z))
cumulative_reward = sum(gamma**i * rewards[:, i] for i in range(h))
td_target = cumulative_reward + gamma**h * Q_theta_target(s_th, next_actions)
# Q函数损失
q_pred = Q_theta(s_t, a_t_to_th)
q_loss = ((q_pred - td_target.detach())**2).mean()
update_network(Q_theta, q_loss)
# 软更新目标网络
soft_update(Q_theta_target, Q_theta, tau=0.005)
# ==================== 在线微调阶段 ====================
current_state = env.reset()
action_chunk = None
step_in_chunk = 0
for step in range(num_online_steps):
# 每h步选择新的动作序列
if step % h == 0:
# 直接从策略网络生成动作序列
z = sample_noise(shape=(action_dim * h,), variance_scale=alpha_h)
action_chunk = mu_phi(current_state.unsqueeze(0), z.unsqueeze(0))
action_chunk = action_chunk.squeeze(0) # 移除batch维度
step_in_chunk = 0
# 执行当前动作
action = action_chunk[step_in_chunk * action_dim:(step_in_chunk + 1) * action_dim]
next_state, reward, done = env.step(action)
# 存储经验并更新网络
replay_buffer.add(current_state, action, reward, next_state, done)
if len(replay_buffer) > batch_size:
update_networks_with_replay_data()
current_state = next_state
step_in_chunk += 1
if done:
current_state = env.reset()
action_chunk = None
step_in_chunk = 0
def sample_noise(shape, variance_scale=1.0):
"""
采样高斯噪声
参数:
- shape: 噪声张量的形状
- variance_scale: 方差缩放因子 α_h
返回: z ~ N(0, I·variance_scale)
"""
return torch.randn(shape) * math.sqrt(variance_scale)
def flow_matching_loss(f_x, states, action_chunks):
"""
流匹配训练损失
目标: 训练 f_x 使其近似离线数据中的行为分布 π_D
"""
# 具体实现依赖于选择的流匹配方法
# 例如: Conditional Flow Matching, Rectified Flow等
pass算法关键点说明
1. 模块化设计
两种算法都采用模块化设计,主要组件包括:
- 行为策略 : f x f_x fx(QC)或流匹配策略(QC-FQL)
- Q函数 : Q θ Q_\theta Qθ,评估动作序列的价值
- 策略网络 :仅QC-FQL需要额外的噪声条件策略 μ ϕ \mu_\phi μϕ
2. 分阶段训练
- 离线阶段:在离线数据上预训练所有组件
- 在线阶段:通过环境交互进行微调,使用经验回放结合离线和在线数据
3. 动作序列执行
实际执行时的关键考虑:
- 每 h h h步重新选择一个动作序列
- 按顺序执行序列中的每个动作
- 处理episode结束时的边界情况
4. 理论保证的实现
- QC方法:通过Best-of-N采样实现KL约束,公式(9)提供理论保证
- QC-FQL方法:通过蒸馏损失实现Wasserstein约束,公式(14)提供上界
这些伪代码提供了实现Q-Chunking的具体指导,读者可以基于这些框架开发自己的实现版本。
七、实验结果与性能分析
实验设置
研究团队在OGBench(Offline-to-online Generalization Benchmark)的5个具有挑战性的长期稀疏奖励域上评估了Q-Chunking方法。这些域包括:
- puzzle-3x3-sparse: 3×3拼图游戏,需要复杂的序列规划
- scene-sparse: 场景导航任务,需要长期空间推理
- cube-double: 双魔方操作,需要精确的动作协调
- cube-triple: 三魔方操作,进一步增加复杂性
- cube-quadruple: 四魔方操作,最高难度的操作任务
性能表现
实验结果显示,Q-Chunking方法在所有测试域上都取得了显著的性能提升:
- 收敛速度:QC方法在大多数任务上比基线方法快2-3倍达到收敛
- 最终性能:在聚合性能指标上,QC方法比最强基线方法(RLPD-AC)提升了约15-20%
- 稳定性:Q-Chunking方法表现出更好的训练稳定性,方差更小
- 泛化能力:该方法在不同复杂度的任务上都保持了一致的性能优势
消融研究
论文进行了详细的消融研究,验证了各个组件的重要性:
动作序列长度 h h h的影响:
- h = 1 h=1 h=1时退化为标准方法,性能较差
- h = 4 − 8 h=4-8 h=4−8时性能最佳,在探索效率和计算成本间取得平衡
- h h h过大时性能下降,可能由于序列预测难度增加
约束强度的影响:
- 过松的约束导致策略偏离有效行为模式
- 过紧的约束限制了必要的探索
- 适中的约束强度能够在利用离线知识和在线探索间取得最佳平衡
八、Q-Chunking的技术优势
1. 探索效率提升
Q-Chunking通过利用离线数据中的时间相干模式,实现了结构化探索:
- 减少无效探索:避免生成明显无效的动作序列
- 加速技能发现:更快地发现和利用有效的行为模式
- 提高样本效率:在有限的在线交互中获得更好的性能
2. 价值传播加速
时间扩展的Q-learning机制实现了有效的长期价值传播:
- 无偏备份:避免了传统n-step方法的异策略偏差问题
- 快速收敛:价值信息能够快速传播到远程状态
- 稳定学习:保持了TD学习的稳定性优势
3. 实现简洁性
Q-Chunking方法具有良好的工程实践特性:
- 模块化设计:各组件相对独立,便于调试和优化
- 通用框架:可以应用于多种现有的offline-to-online算法
- 参数可控:关键超参数具有明确的物理意义,便于调节
4. 理论保证
两种实现方案都提供了坚实的理论基础:
- QC方法:KL散度上界(公式9)保证了约束的有效性
- QC-FQL方法:Wasserstein距离约束(公式14)提供了几何直观的理解
- 收敛性:在标准假设下,方法具有收敛性保证
九、局限性与未来方向
当前局限性
- 计算开销:Best-of-N采样增加了推理时的计算成本
- 超参数敏感性:动作序列长度和约束强度需要仔细调节
- 离线数据质量依赖:方法性能很大程度上依赖于离线数据的质量和多样性
未来研究方向
- 自适应序列长度:根据任务复杂度动态调整动作序列长度
- 层次化扩展:结合层次强化学习,处理更复杂的长期任务
- 多模态应用:扩展到视觉-语言-动作的多模态学习场景
- 在线适应:开发能够在线调整约束强度的自适应机制
十、结论
Q-Chunking为强化学习领域带来了一个重要的技术创新。通过将传统的单步决策扩展到动作序列级别,该方法成功地解决了长期稀疏奖励任务中的探索难题。
核心贡献总结
-
概念创新:首次将动作分块技术系统性地应用于时间差分强化学习,开创了序列级RL的新范式
-
技术突破:设计了无偏的h-step价值备份机制,在保持学习稳定性的同时显著加速收敛
-
实用价值:提供了两种具体实现方案(QC和QC-FQL),具有良好的理论保证和实际性能
-
通用框架:方法可以应用于多种现有的offline-to-online算法,具有广泛的适用性
技术意义
Q-Chunking的提出不仅解决了特定的技术问题,更重要的是为强化学习研究提供了新的思路。它表明,通过合理利用离线数据中的时间结构信息,可以显著提升在线学习的效率。这一思想对于开发更加智能和高效的AI系统具有重要启发意义。
实际应用前景
随着机器人技术和自动化系统的快速发展,Q-Chunking方法在以下领域具有广阔的应用前景:
- 机器人操作:复杂的操作任务通常需要精确的动作序列协调
- 游戏AI:策略游戏和实时游戏中的长期规划
- 自动驾驶:需要连续动作决策的驾驶场景
- 工业控制:需要序列化操作的生产流程控制
Q-Chunking方法的成功展示了将传统机器学习技术与领域特定知识相结合的巨大潜力。通过深入理解问题的时间结构特性,我们能够设计出更加有效和实用的解决方案。
对于研究者和工程师而言,Q-Chunking不仅提供了一个强大的技术工具,更重要的是展示了一种系统性思考复杂序列决策问题的方法论。这种方法论的价值将随着AI技术在更多复杂现实场景中的应用而日益凸显。
参考文献
1\] Li, Q., Zhou, Z., \& Levine, S. (2025). Reinforcement Learning with Action Chunking. *arXiv preprint arXiv:2507.07969*. https://arxiv.org/pdf/2507.07969 \[2\] Nakano, R., Hilton, J., Balaji, S., Wu, J., Ouyang, L., Kim, C., ... \& Schulman, J. (2021). WebGPT: Browser-assisted question-answering with human feedback. *arXiv preprint arXiv:2112.09332*.