文章目录
- [1. MAE与MSE的本质区别](#1. MAE与MSE的本质区别)
- [2. 高斯噪声下的统计特性](#2. 高斯噪声下的统计特性)
- [3. MAE导致稀疏解的内在机制](#3. MAE导致稀疏解的内在机制)
- [4. 对比总结](#4. 对比总结)
1. MAE与MSE的本质区别
MAE(Mean Absolute Error)和MSE(Mean Squared Error)是两种常用的损失函数,它们的数学形式决定了对误差的不同敏感程度:
- MAE : MAE = 1 n ∑ i = 1 n ∣ y i − y ^ i ∣ \text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i| MAE=n1∑i=1n∣yi−y^i∣
- MSE : MSE = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 MSE=n1∑i=1n(yi−y^i)2
从几何角度看,MSE等价于欧氏距离的平方,而MAE等价于曼哈顿距离。这导致MSE对离群点更加敏感,而MAE更具鲁棒性。
2. 高斯噪声下的统计特性
在噪声服从高斯分布 ϵ ∼ N ( 0 , σ 2 ) \epsilon \sim \mathcal{N}(0, \sigma^2) ϵ∼N(0,σ2) 的假设下:
-
MSE是最优损失函数
MSE对应于高斯噪声下的最大似然估计(MLE)。此时,最小化MSE等价于最大化对数似然函数:
arg min θ ∑ i = 1 n ( y i − f ( x i ; θ ) ) 2 ⇔ arg max θ ∏ i = 1 n 1 2 π σ 2 exp ( − ( y i − f ( x i ; θ ) ) 2 2 σ 2 ) \arg\min_{\theta} \sum_{i=1}^{n} (y_i - f(x_i; \theta))^2 \quad \Leftrightarrow \quad \arg\max_{\theta} \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(y_i - f(x_i; \theta))^2}{2\sigma^2}\right) argθmini=1∑n(yi−f(xi;θ))2⇔argθmaxi=1∏n2πσ2 1exp(−2σ2(yi−f(xi;θ))2)高斯分布的二次指数形式直接对应平方误差。
-
MAE的统计假设
MAE对应于噪声服从拉普拉斯分布时的MLE。拉普拉斯分布的概率密度函数为:
p ( ϵ ) = 1 2 b exp ( − ∣ ϵ ∣ b ) p(\epsilon) = \frac{1}{2b} \exp\left(-\frac{|\epsilon|}{b}\right) p(ϵ)=2b1exp(−b∣ϵ∣)arg min θ ∑ i = 1 n ∣ y i − f ( x i ; θ ) ∣ ⇔ arg max θ ∏ i = 1 n 1 2 b exp ( − ∣ y i − f ( x i ; θ ) ∣ b ) \arg\min_{\theta} \sum_{i=1}^{n} |y_i - f(x_i; \theta)| \quad \Leftrightarrow \quad \arg\max_{\theta} \prod_{i=1}^{n} \frac{1}{2b} \exp\left(-\frac{|y_i - f(x_i; \theta)|}{b}\right) argθmini=1∑n∣yi−f(xi;θ)∣⇔argθmaxi=1∏n2b1exp(−b∣yi−f(xi;θ)∣)
此时,最小化MAE等价于最大化拉普拉斯分布下的对数似然。
3. MAE导致稀疏解的内在机制
MAE容易产生稀疏解的根本原因在于其梯度特性:
-
MAE的梯度恒定
MAE的梯度为:
∂ MAE ∂ θ = { + 1 , if y i − f ( x i ; θ ) > 0 − 1 , if y i − f ( x i ; θ ) < 0 undefined , if y i − f ( x i ; θ ) = 0 \frac{\partial \text{MAE}}{\partial \theta} = \begin{cases} +1, & \text{if } y_i - f(x_i; \theta) > 0 \\ -1, & \text{if } y_i - f(x_i; \theta) < 0 \\ \text{undefined}, & \text{if } y_i - f(x_i; \theta) = 0 \end{cases} ∂θ∂MAE=⎩ ⎨ ⎧+1,−1,undefined,if yi−f(xi;θ)>0if yi−f(xi;θ)<0if yi−f(xi;θ)=0当参数接近零时,梯度仍保持恒定(±1),促使参数快速收敛到零。
-
MSE的梯度衰减
MSE的梯度为:
∂ MSE ∂ θ = − 2 ( y i − f ( x i ; θ ) ) ⋅ ∂ f ( x i ; θ ) ∂ θ \frac{\partial \text{MSE}}{\partial \theta} = -2(y_i - f(x_i; \theta)) \cdot \frac{\partial f(x_i; \theta)}{\partial \theta} ∂θ∂MSE=−2(yi−f(xi;θ))⋅∂θ∂f(xi;θ)当误差接近零时,梯度趋近于零,导致参数更新变得非常缓慢,难以彻底消除小参数。
-
几何解释
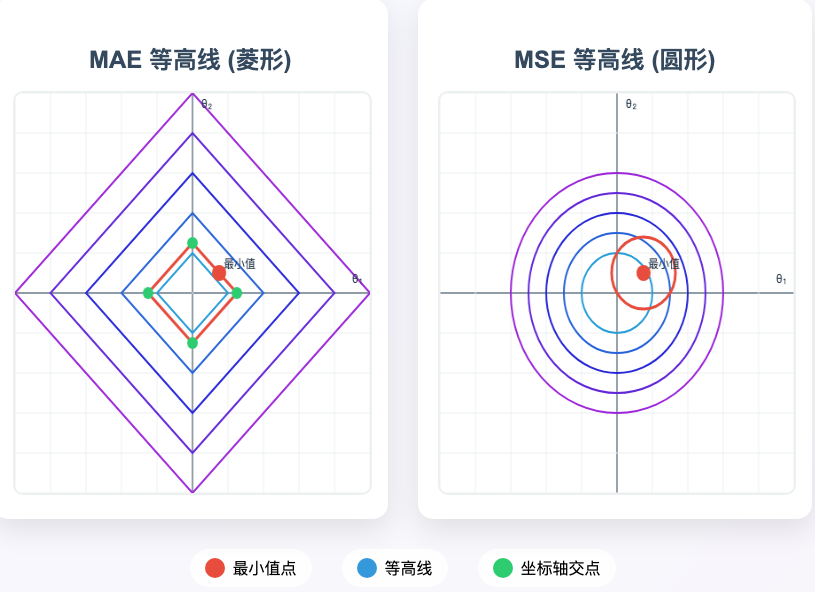
从优化角度看,MAE的等高线是菱形(在二维空间中),其顶点位于坐标轴上;而MSE的等高线是圆形。当损失函数的最小值靠近坐标轴时,MAE的等高线更容易与坐标轴相交,从而使某些参数被置零。更多可见 损失函数的等高线与参数置零的关系
4. 对比总结
| 特性 | MSE | MAE |
|---|---|---|
| 对离群点敏感度 | 高(平方放大误差) | 低(线性处理误差) |
| 噪声分布假设 | 高斯分布 | 拉普拉斯分布 |
| 梯度特性 | 梯度随误差减小而衰减 | 梯度恒定(除零点外) |
| 稀疏性 | 不易产生稀疏解 | 易产生稀疏解 |
| 优化稳定性 | 平滑优化,数值稳定性好 | 非光滑优化,可能需要特殊处理 |
在实际应用中,如果数据包含较多离群点或需要进行特征选择,MAE是更合适的选择;如果追求预测精度且噪声近似高斯分布,MSE通常表现更好。