排序初识（上）-- 讲解超详细

日常生活中我们对于排序并不陌生，小时候的排大小数字，体育课的身高排序，年龄排序等等，都是排序的体现，那如何用代码实现排序呢？这里有很多种方法等待解锁。

1. 排序的概念

概念：排序是计算机内经常进行的一种操作，其目的是将一组"无序"的记录序列调整为"有序"的记录序列。

1.2 排序的应用

身高排序

数字排序

1.3 常见排序算法

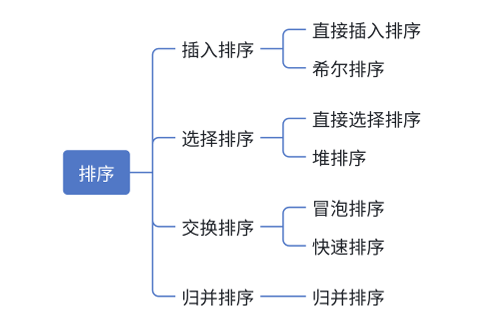
下面依次来介绍这几种排序

2. 实现常见的排序算法

2.1 插入排序

2.1.1 直接插入排序

大家应该都玩过扑克牌吧，扑克牌可以发牌也可以摸牌，我们摸一张牌之后是不是要对手中的牌，进行排序，可以是从牌3 -> 王炸，也可以是从王炸 -> 牌3，直接插入排序就和这种摸牌的思想一样。我们画个图分析一下：

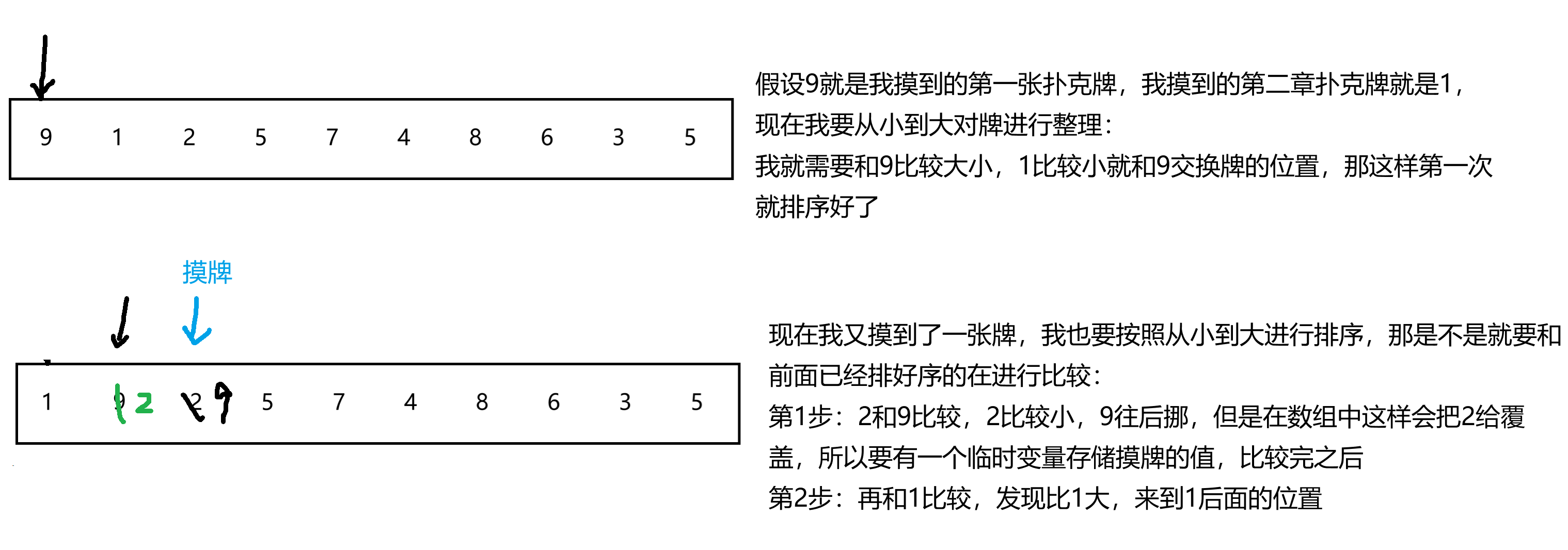
思路大概就是这样

1.假设数组存放，从下标 i = 0的位置开始，arr[i+1]存放到tmp变量；

2.tmp和前面的数据依次进行比较，如果交换，i--继续和前一个元素比较，直到排完序！

代码实现

//直接插入排序
void InsertSort(int* arr, int n)
{
	int i = 0;
	for (i = 0; i < n-1; i++)
	{
		int end = i;
		int tmp = arr[end + 1];//始终保存下一个数据
		//插入一张牌，调整一轮
		while (end >= 0)
		{
			if (arr[end] > tmp)
			{
				arr[end + 1] = arr[end];
				end--;
			}
			else
			{
				break;
			}
		}
		//end < 0;
		arr[end + 1] = tmp;
	}
}

2.1.1.1 直接插入排序时间复杂度

时间复杂度：O(N^2)

空间复杂度：O(1)

2.1.2 希尔排序

定义：希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至 1 时，整个文件恰被分成一组，算法便终止。

看着懵懵的，叽里咕噜说的是个啥呢？ -- 看不懂

没关系，我慢慢告诉你，希尔排序就是再直接插入排序的基础上进行了优化，是怎么个优化方法呢？我们先来分析他的时间复杂度！！！

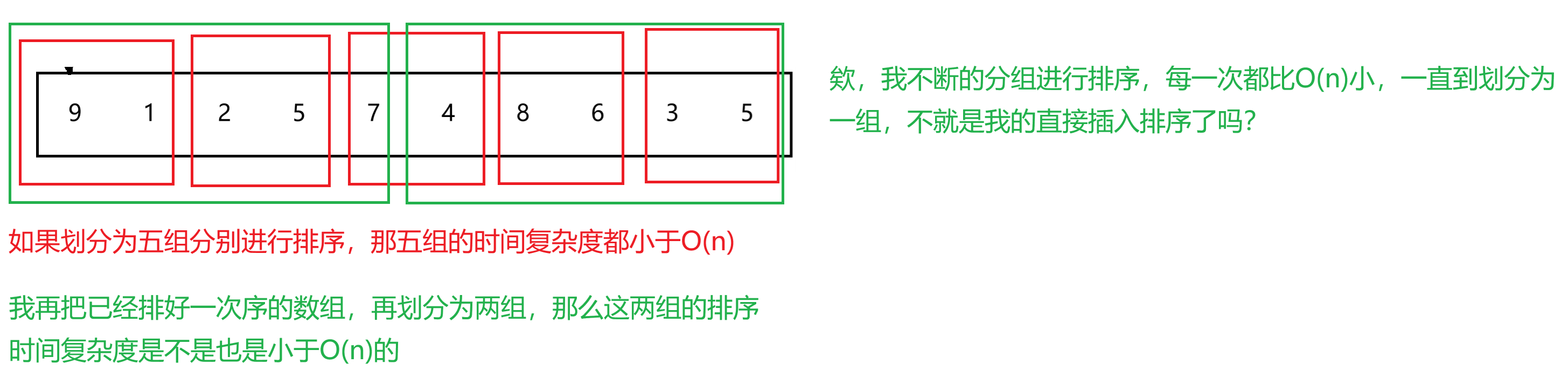
这时有人会说，最后一组的时候都变成直接插入排序了，你为什么说时间复杂度变小了呢？

欸同学，你划分到最后只剩一组的时候不就是快有序的情况了吗？这种场景下排序不久很快了嘛？！ 可能这种情况下，就交换一次或者两次的。

发现没有，当我数组越接近有序的时候我直接插入效率就更高了！！！

所以希尔排序再其基础上改进，它的效率肯定是要高于直接插入排序的！！

这里也写一下，直接插入排序的时间复杂度：时间复杂度：O(N^2）

咳咳不啰嗦了，开始进入正题：

希尔排序是怎么进行改进优化的？

希尔排序法的基本思想是：先选定⼀个整数（通常是gap=n/3+1），把待排序文件所有记录分成各组，所有的距离相等的记录分在同一组内，并对每⼀组内的记录进行排序，然后gap=gap/3+1得到下一个整数，再将数组分成各组，进行插入排序，当gap=1时，就相当于直接插入排序

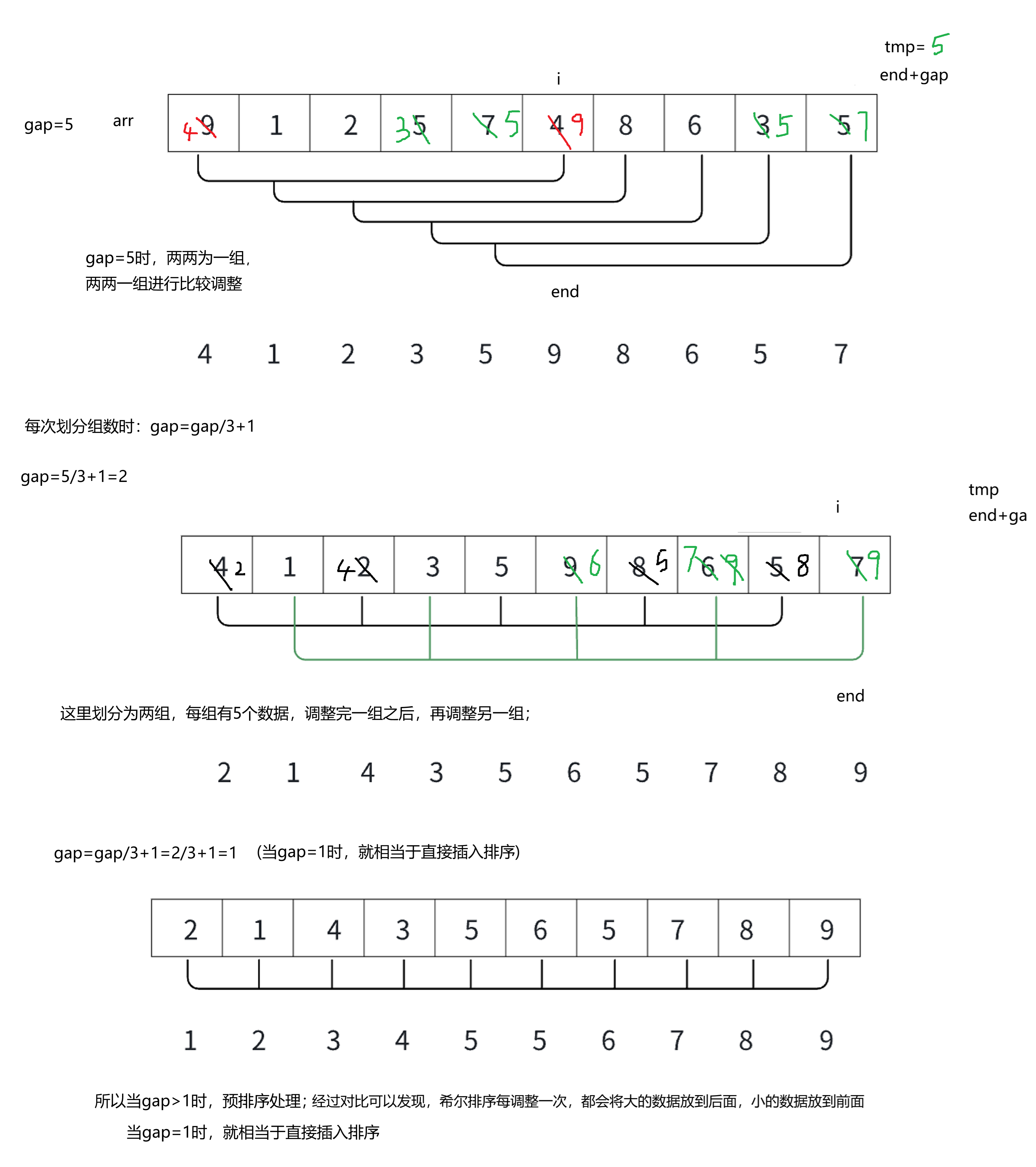
如果一组比完在比较一组，会嵌套很多循环，如何改进代码?

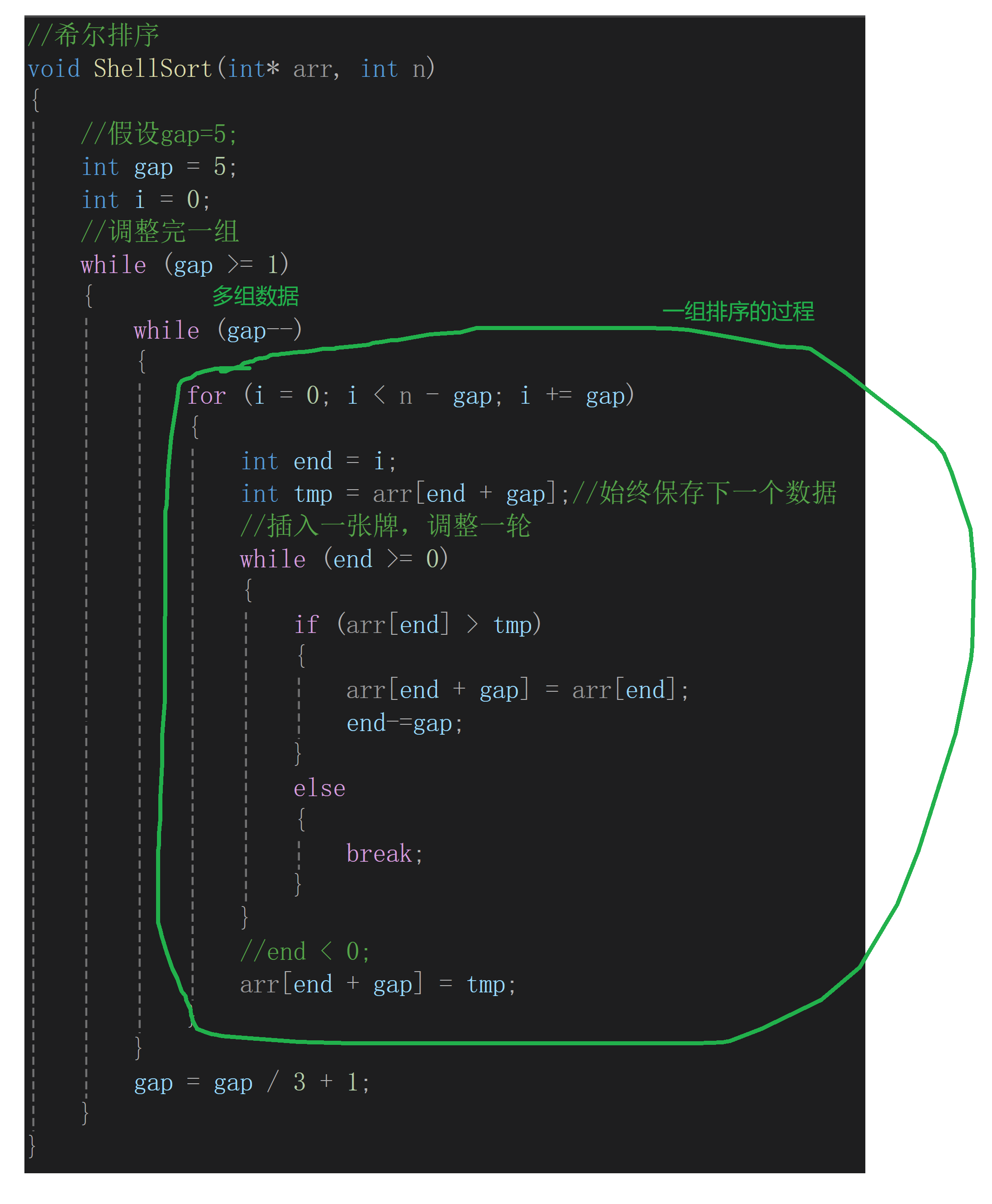
优化方法：让第1组第1个数据和第1组第2个数据比较，再i++，比较第2组第1个数组和第2组第2个数据；再比较第一组第1个和第2个和第3个数据比较，同理第2组也是，这样就可以不用那么多循环了！！

千万注意：gap进入循环的条件不能 >= 1，如果gap==1，gap/3+1就会一直为1，会死循环！！！

代码实现

//希尔排序
void ShellSort(int* arr, int n)
{
	int gap = n;
	while (gap > 1)//这里gap不能等于1，如果等于1会死循环
	{
		gap = gap / 3 + 1;//再次重新分组
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = arr[end + gap];//始终保存下一个数据
			//插入一张牌，调整一轮
			while (end >= 0)
			{
				if (arr[end] > tmp)
				{
					arr[end + gap] = arr[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			//end < 0;
			arr[end + gap] = tmp;
		}
	}
}

2.1.2.1 希尔排序时间复杂度

外层循环：

由于gap=gap/3+1，那第1次：n/3 -> 第2次：n/3/3 -> 第3次：n/3/3/3-> 第k次：n/3/3/3/....

相当于log3(n)，这就是外层时间复杂度 。

内层循环：

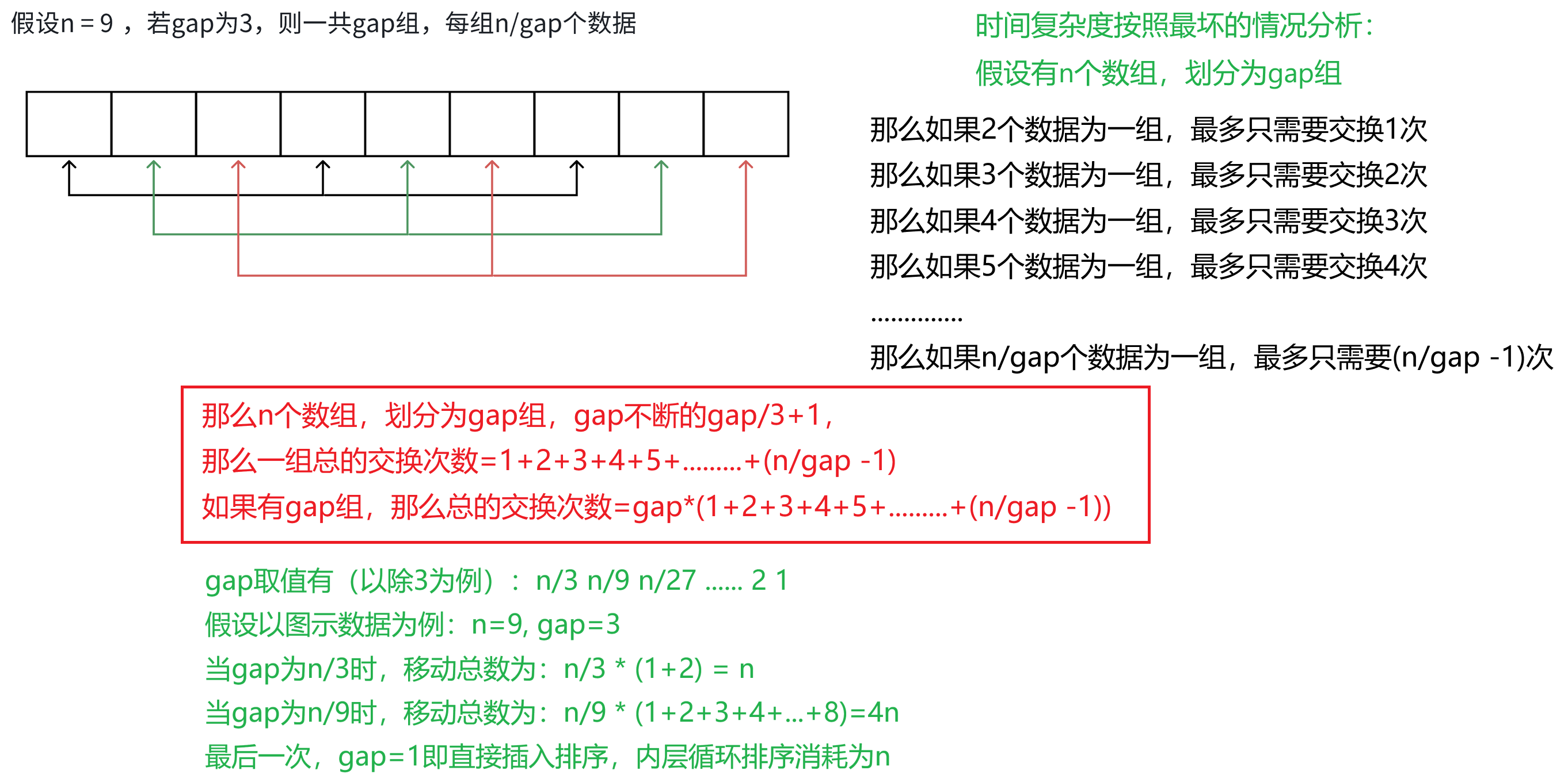
gap的取值不一样，会产生不一样的计算结果，所以希尔排序时间复杂度很难有一个确定的值。

这里引用《数据结构(C语言版)》---严蔚敏书中给出的时间复杂度为：

2.2 选择排序

概念：在一堆数据中选出最大/最小的数据，放在序列的起始位置，直到所有数据有序。

2.2.1 直接选择排序

直接选择排序和概念的讲述是一样，我们主要分析实现过程。

既然我们要选择找最大值/最小值，不妨创建两个临时变量来保存最大/小的下标（比如：maxi，mini），因为排序一端是最大值，另一端是最小值，如果找到了，我们就把它们放到开头和结尾。

所以我们从头和尾同时遍历（begin，end），找到最大/小值，将最小值放到头，最大值放到尾，此时begin++，end++，因为头尾已经确定无需再遍历。重复过程，直到我的begin >= end，不在继续比较！！！

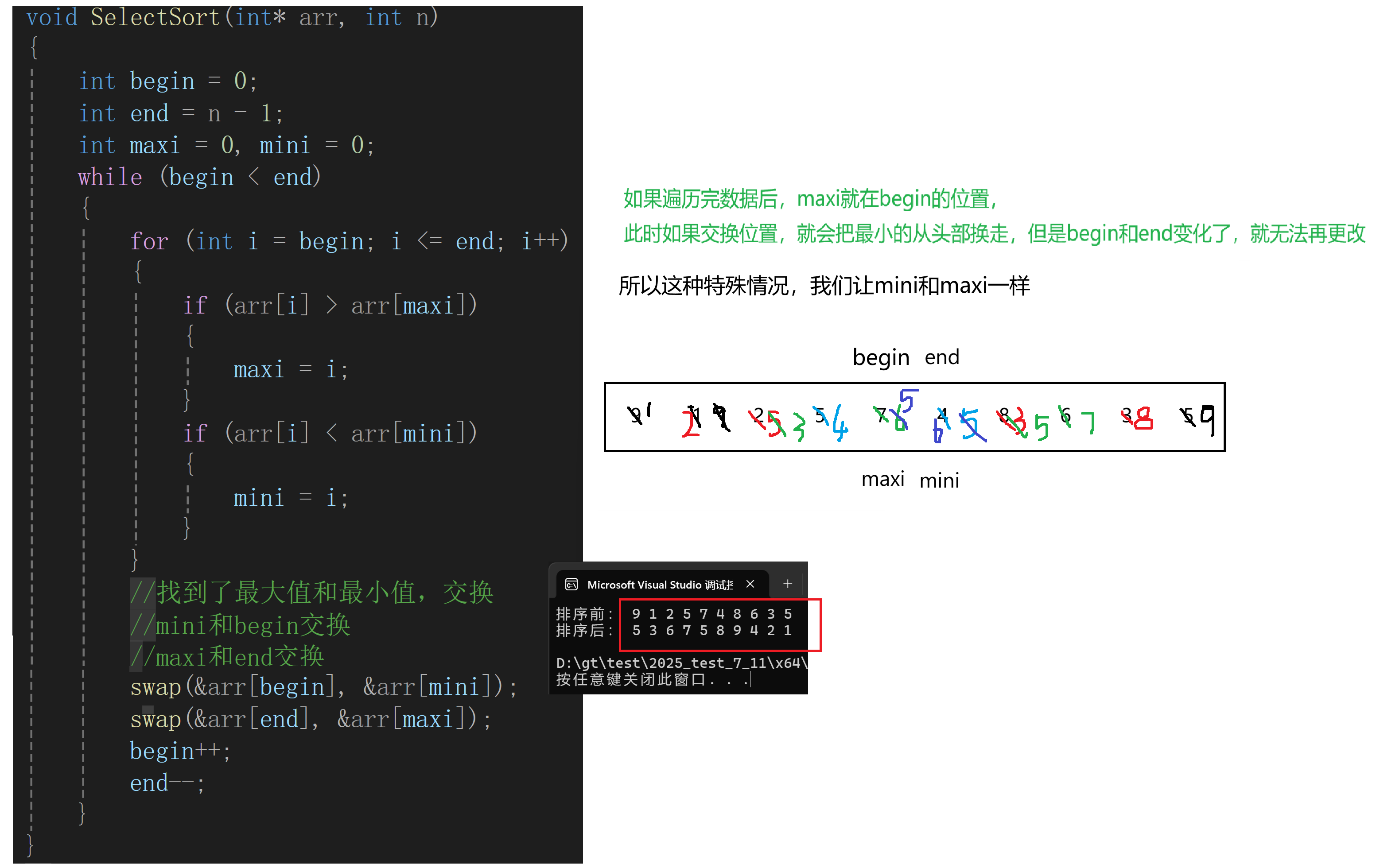注意：当maxi遍历完还在begin位置的时候，此时min和begin交换，把max改成了最小值，max和end交换，最小值来到了末尾，还不能再次修改，因为end--了。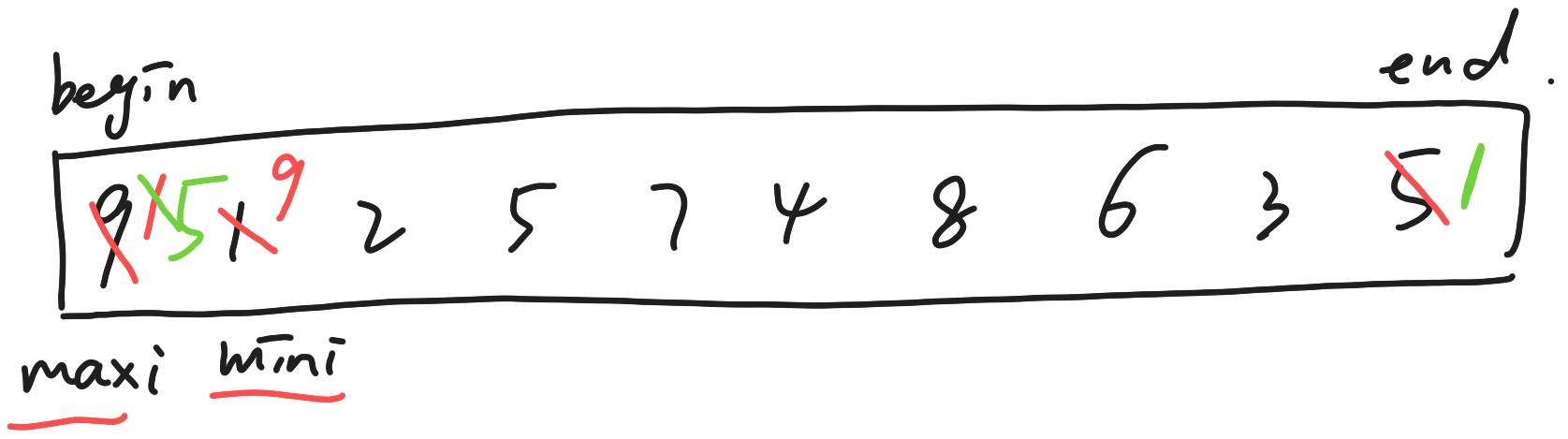

代码实现：

//直接选择排序
void SelectSort(int* arr, int n)
{
	int begin = 0;
	int end = n - 1;
	int maxi = 0, mini = 0;
	while (begin < end)
	{
		for (int i = begin; i <= end; i++)
		{
			if (arr[i] > arr[maxi])
			{
				maxi = i;
			}
			if (arr[i] < arr[mini])
			{
				mini = i;
			}
		}
		//如果maxi在begin的位置
		if (maxi == begin)
		{
			maxi = mini;
		}
		//找到了最大值和最小值，交换
		//mini和begin交换
		//maxi和end交换
		swap(&arr[begin], &arr[mini]);
		swap(&arr[end], &arr[maxi]);
		begin++;
		end--;
	}
}

2.2.1.1 直接选择排序时间复杂度

时间复杂度： O(N^2)

空间复杂度： O(1)

2.3 堆排序

堆排序就是找到最后一棵子树，利用向上/下调整算法变成有效的堆，在交换堆顶和最后一个元素，就可以得到有序的结果（从小到大：建大堆，从大到小：建小堆）

这里实现过程可以查看前面的堆应用讲解，这里不再实现了。

2.4 交换排序

有同学看到交换排序就会想起交换两个数，例如交换两个数，当时还说了为什么不能传值调用，简单回顾一下，传值调用时对实参的拷贝，改变的是形参不会影响实参！

void swap(int* x, int* y)
{
	int tmp = *x;
	*x = *y;
	*y = tmp;
}

但是很遗憾这并不是真正的交换排序，什么是真正的交换排序？

所谓交换，就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置交换排序的特点是：将键值较大的记录向序列的尾部移动，键值较小的记录向序列的前部移动。

可以想一想之前的冒泡排序

2.4.1 冒泡排序

思路如图：

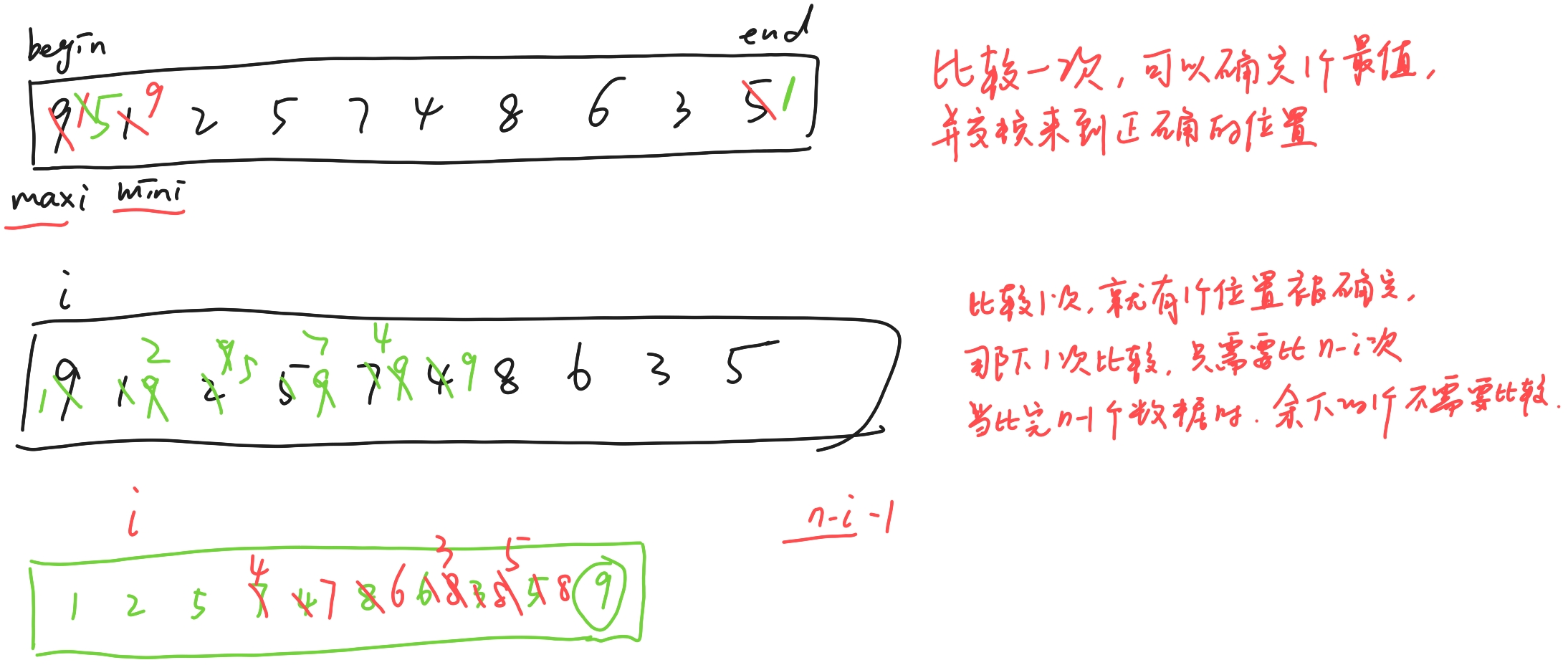
代码实现：

void BubbleSort(int* a, int n) 
{
    int exchange = 0;
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j <n-i-1 ; j++)
        {
            if (a[j] > a[j + 1]) 
            {
                exchange = 1;
                swap(&a[j], &a[j + 1]);
            }
        }
        if (exchange == 0) 
        {
            break;
        }
    }
 }