常见代码八股

1. 利用梯度下降法，计算二次函数y=x^2+x+4的最小值

python 复制代码

def target_function(x):
    return x ** 2 + x +4

def gradient(x):
    return 2*x + 1

x_init = 10
x = x_init
steps = 100
lr = 0.1
for i in range(100):
    x = x - lr*gradient(x)

print(f"最小值 f(x) = {target_function(x):.4f}")

2. 实现交叉熵损失、Softmax以及Sigmoid

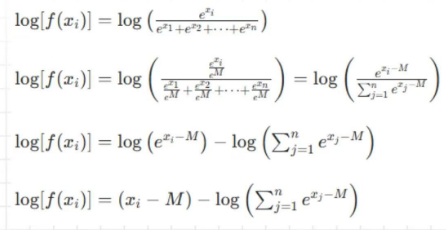
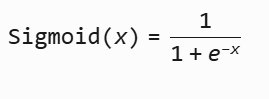
python 复制代码

#实现Softmax、Logsoftmax、Sigmoid以及交叉熵损失
import torch
import torch.nn.functional as F

def softmax(x, dim=-1):
    exp_x = torch.exp(x)
    return exp_x/torch.sum(exp_x, dim=dim, keepdim=True)

# 1.上溢出问题：当x趋向于无穷大时，会导致exp(x)超过数值范围
# 2.下溢出问题：当x趋向于负无穷大时，会导致exp(x)被截断变成0，加上log会出现log(0)的情况。所以要避免单独计算exp(x)
# 解决方案：1. 减掉最大值 2. 计算log时先拆开

def log_softmax(x, dim=-1):
    x = x - torch.max(x,dim=-1,keepdim=True)[0]
    return x - torch.log(torch.sum(torch.exp(x),dim=-1,keepdim=True))

# x = torch.rand((2,3))
# print(torch.allclose(F.softmax(x,dim=-1),softmax(x)))
# print(torch.allclose(log_softmax(x),torch.log(softmax(x))))
# print(torch.allclose(F.log_softmax(x,dim=-1),log_softmax(x)))

def sigmoid(x):
    return 1/(1+torch.exp(-x))

# print(torch.allclose(torch.sigmoid(x),sigmoid(x)))

def cross_entropy_loss(y_pred, y_true):
    y_pred = log_softmax(y_pred,dim=-1)
    return -torch.sum(y_true*y_pred, dim=-1)

# input = torch.rand((2,3))
# label_onehot = torch.tensor([[0,0,1],[0,1,0]])
# print(cross_entropy_loss(input,label_onehot))

# # pytorch内置的cross_entropy_loss的输入是类别索引，不是one hot向量

# label = torch.argmax(label_onehot,dim=-1)
# offi_cross_entropy_loss = torch.nn.CrossEntropyLoss(reduction="none")

# print(torch.allclose(offi_cross_entropy_loss(input,label), cross_entropy_loss(input,label_onehot)))
# print(offi_cross_entropy_loss(input,label))