🍭lc2039.bfs+空闲时间
把网络抽象成图,用 BFS 算出 0 号节点到各节点的最短距离 d 。
结合每个节点发消息的间隔 patience[v] ,先算消息往返需要 2d 秒。
再看 2d 和 patience[v] 的关系
- 若 2d 能被 patience[v] 整除,最后一条消息已发时长 t 就是 patience[v] ;
- 若不能整除,t 是 2d % patience[v] 。
接着算出节点收到最后一条回复的时间是 4d - t ,下一秒 ++4d - t + 1++ 就是节点变空闲的最早时间。
所有++节点里时间的最大值,就是整个网络变空闲的时间 。++

class Solution {
public:
int networkBecomesIdle(vector<vector<int>>& edges, vector<int>& patience)
{
int n = patience.size();
vector<vector<int>> g(n);
for (auto& e : edges)
{
int v = e[0], w = e[1];
g[v].push_back(w);
g[w].push_back(v);
}
vector<bool> vis(n, false);
vis[0] = true;
queue<int> q;
q.push(0);
int ans = 0;
for (int d = 0; !q.empty(); d++)
{
int size = q.size();
for (int i = 0; i < size; i++)
{
int v = q.front();
q.pop();
if (v > 0)
{
int p = patience[v];
//两种情况求t
++int t = p;
if (2 * d % p > 0)++
++{
t = 2 * d % p;
}++
++ans = max(ans, 4 * d - t + 1);++
}
for (int w : g[v])
{
if (!vis[w])
{
vis[w] = true;
q.push(w);
}
}
}
}
return ans;
}
};
🍭lc847.状态压缩+多源bfs
多源bfs+位图记录每一条走过的路径,当有一条路径经过所有点时最短路径找到

class Solution {
public:
int shortestPathLength(vector<vector<int>>& graph) {
const int n = graph.size();
++const int ans = (1 << n) -1;++
queue<pair<int,int>> q;
vector<vector<int>> visit(n, vector<int>(1 << n));
int step = 0;
for (int i = 0; i < n; i++)
{
++q.push({i, 1 << i});++
}
while (!q.empty())
{
int qsz = q.size();
for (int i = 0; i < qsz; i++)
{
auto p = q.front();
q.pop();
++int node = p.first;
int state = p.second;++
++if (state == ans) return step;
if (visit[node][state] == 1) continue;++
for (auto next : graph[node])
{
q.push({next, state|(1 << next)});
}
visit[node][state] = 1;
}
step++;
}
return -1;
}
};
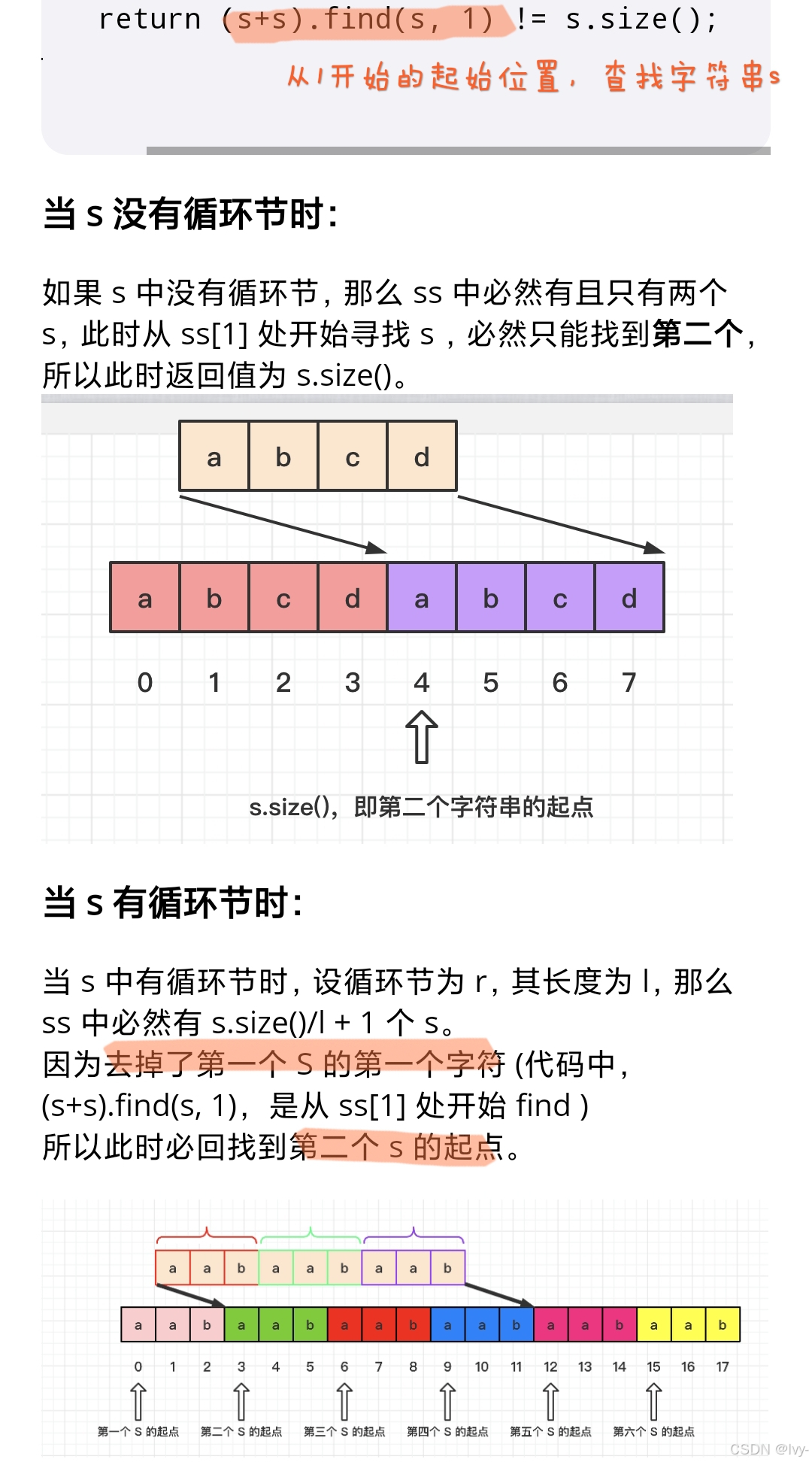
lc459.双倍字符串
++return (s+s).find(s, 1) != s.size();++
str.find(要找的子串, 开始查找的位置) ,返回的是子串第一次出现的起始索引;如果没找到,就返回一个特殊值( string::npos )
class Solution {
public:
bool repeatedSubstringPattern(string s) {
++return (s+s).find(s, 1) != s.size();++
}
};
啪很快,上来就写了一个暴力...
class Solution {
public:
bool repeatedSubstringPattern(string s) {
int n=s.size();
for(int i=1;i<=n/2;i++)
{
if(n%i==0)
{
string check=s.substr(0,i);
int hand=i;
while(hand<=n)
{
string tmp=s.substr(hand,i);
if(tmp!=check)
break;
hand+=i;
}
if(hand>=n) return true;
}
}
return false;
}
};
lc367.完全平方数
闭区间二分(三步)
++[0,n-1]. l<=r . l r mid+-1++
注意long long
class Solution {
public:
bool isPerfectSquare(int num)
{
int n=num/2;
int l=0,r=n;
while(l<=r)
{
long long mid=l+(r-l)/2;
if(mid*mid>num)
r=mid-1;
else if(mid*mid==num)
return true;
else
l=mid+1;
}
return (long long)l*l==num;
}
};
lc448.消失的数字 o(n)
处理到理应位置后judge

class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
vector<int> res;
int i = 0;
while (i < nums.size())
{
++if (nums[i] == i + 1)++
{
i++;
continue;
}
int idealIdx = nums[i] - 1;
++if (nums[i] == nums[idealIdx])++
{
i++;
continue;
}
//例如 实现把数字3放到索引2的位置
int tmp = nums[i];
nums[i] = nums[idealIdx];
nums[idealIdx] = tmp;
}
for (int i = 0; i < nums.size(); i++)
{
if (nums[i] != i+1)
{ //未处理
res.push_back(i+1);
}
}
return res;
}
};
原代码 nlogn了...
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums)
{
vector<int> ret;
int n=nums.size();
sort(nums.begin(),nums.end());
int k=nums.back();
int j=1;
for(int i=0;i<n;i++)
{
while(nums[i]>j)
{
ret.push_back(j);
j++;
}
if(j==nums[i]) j++;
}
while(k<n)
ret.push_back(++k);
return ret;
}
};
lc231.二的幂
++二进制最高位为1,其余所有位为0++
++(n & (n - 1)) == 0 true++
循环写法
class Solution {
public:
bool isPowerOfTwo(int n)
{
while(n)
{
if(n==1) return true;
if(n&1) return false;
n>>=1;
}
return false;
}
};
计算机视角
class Solution {
public:
bool isPowerOfTwo(int n) {
return n > 0 && ++(n & (n - 1)) == 0;++
}
};
lc25
三指针,迭代翻转链表
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
ListNode* tmp = head;
int n = 0;
// 计算链表长度
while (tmp) {
n++;
tmp = tmp->next;
}
if (n < k) return head;
ListNode* newHead = nullptr;
ListNode* cur = head;
ListNode* prevTail = nullptr;
// 分组处理
while (n >= k) {
ListNode* groupHead = cur;
ListNode* prev = nullptr;
ListNode* tail = cur;
// 翻转一组 k 个节点
for (int i = 0; i < k; i++) {
ListNode* next = cur->next;
cur->next = prev;
prev = cur;
cur = next;
}
if (!newHead) {
newHead = prev;
}
if (prevTail) {
prevTail->next = prev;
}
prevTail = tail;
n -= k;
}
// 连接剩余节点
if (cur) {
prevTail->next = cur;
}
return newHead;
}
// 原 reverse 函数递归实现有问题,这里用迭代方式重写(也可继续用递归,不过迭代更直观)
ListNode* reverse(ListNode* head) {
ListNode* prev = nullptr;
ListNode* cur = head;
while (cur) {
ListNode* next = cur->next;
cur->next = prev;
prev = cur;
cur = next;
}
return prev;
}
};