目标:用4×4矩阵把1个点从 (2, 3, 4) 平移到 (5, 3, 4)(即x方向+3)
第1步:齐次坐标表示( 齐次坐标是给普通3D坐标 (x,y,z) 加一个魔法数字 w ,变成 (x,y,z,w),让计算机能统一处理移动、旋转、缩放和透视**)**
-
普通3D坐标 :
(2, 3, 4) -
齐次坐标 :加一个
w=1→(2, 3, 4, 1)(
w=1代表"这是一个点",w=0代表"方向",比如光线)
第2步:构造平移矩阵
要移动 (x+3, y+0, z+0),对应的4×4矩阵是:

解读:
-
左上角3×3部分(
1,0,0; 0,1,0; 0,0,1)负责旋转/缩放(这里不变)。 -
最右边一列
(3, 0, 0, 1)负责平移 (x+3)。
第3步:矩阵乘法计算
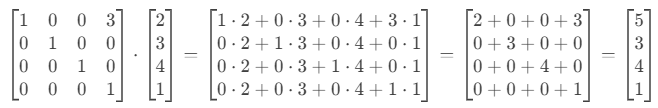
结果 :(5, 3, 4, 1) → 去掉 w 就是 (5, 3, 4),平移成功!
Q1:为什么不能直接用3×3矩阵?
- 尝试用3×3矩阵做平移:
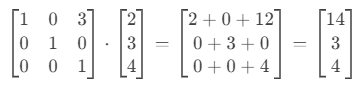
错误! 结果 (14, 3, 4) 不是我们想要的 (5, 3, 4)。
原因 :3×3矩阵的平移项会乘以 z 值(这里 3×4=12),无法单独加3。
Q2:w=0 时会发生什么?
- 如果是方向向量
(2, 3, 4, 0)(比如光线方向):
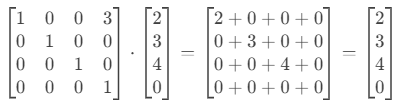
结果不变! 因为 w=0 让平移失效(方向向量不受位置影响)。