Leetcode题解：739每日温度，用单调栈解决问题！

一、题目内容

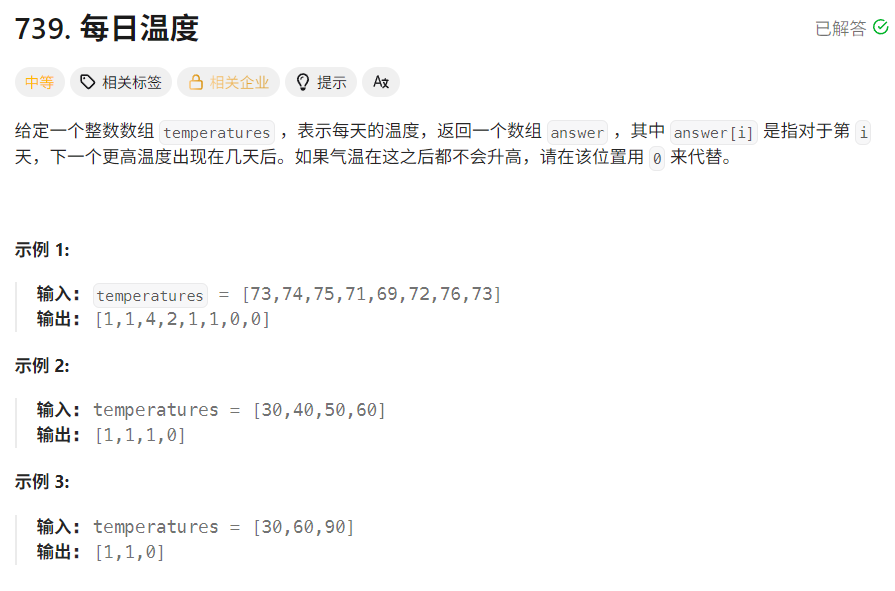
题目要求根据给定的温度数组 temperatures，返回一个数组 answer，其中 answer[i] 表示对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，则在该位置用 0 来代替。

二、题目分析

输入和输出

输入：

一个整数数组 temperatures，表示每天的温度。

输出：

一个整数数组 answer，其中 answer[i] 表示对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，则在该位置用 0 来代替。

算法逻辑

使用单调栈（Monotonic Stack）来解决这个问题。单调栈是一种特殊的栈结构，用于处理数组中的顺序问题，特别是找到下一个更大或更小的元素。

初始化：
- 创建一个结果数组 result，大小与 temperatures 相同，所有元素初始化为 0。
- 创建一个栈 stack，用于存储温度的索引。
遍历温度数组：
- 遍历 temperatures，对于每个温度 temperatures[i]：
  - 如果栈不为空且当前温度 temperatures[i] 大于栈顶索引对应的温度 temperatures[stack.top()]，则：
    - 弹出栈顶索引 pre。
    - 计算索引差值 i - pre，并将其存储到 result[pre] 中。
  - 将当前索引 i 压入栈中。
返回结果：
- 如果某个位置的温度之后没有更高的温度，则 result 中该位置的值保持为 0。
- 返回 result。

三、解题要点

单调栈的定义：
- 单调栈是一种特殊的栈结构，用于处理数组中的顺序问题，特别是找到下一个更大或更小的元素。
栈的使用：
- 栈用于存储温度的索引。
- 当前温度大于栈顶索引对应的温度时，弹出栈顶索引，并计算索引差值。
结果数组的初始化：
- 结果数组 result 的大小与 temperatures 相同，所有元素初始化为 0。
算法复杂度：
- 时间复杂度：O(n)，每个元素最多被压入和弹出栈一次。
- 空间复杂度：O(n)，用于存储结果数组和栈。

四、代码解答

以下是使用单调栈算法的 C++ 实现代码：

复制代码

#include <vector>
#include <stack>

using namespace std;

class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& temperatures) {
        vector<int> result(temperatures.size(), 0); // 初始化结果数组
        stack<int> stack; // 用于存储温度的索引

        for (int i = 0; i < temperatures.size(); ++i) {
            // 当前温度大于栈顶索引对应的温度
            while (!stack.empty() && temperatures[i] > temperatures[stack.top()]) {
                int pre = stack.top(); // 栈顶索引
                stack.pop(); // 弹出栈顶索引
                result[pre] = i - pre; // 计算索引差值
            }
            stack.push(i); // 当前索引入栈
        }

        return result;
    }
};

五、详细注释

单调栈的作用：
- 单调栈用于处理数组中的顺序问题，特别是找到下一个更大或更小的元素。
- 在这个问题中，单调栈用于找到每个温度之后的第一个更高温度。
栈的维护：
- 栈用于存储温度的索引。
- 当前温度大于栈顶索引对应的温度时，弹出栈顶索引，并计算索引差值。
结果数组的初始化：
- 结果数组 result 的大小与 temperatures 相同，所有元素初始化为 0。
- 如果某个位置的温度之后没有更高的温度，则 result 中该位置的值保持为 0。
终止条件：
- 如果某个位置的温度之后没有更高的温度，则 result 中该位置的值保持为 0。
- 返回结果数组 result。

六、代码执行过程示例

假设我们有 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]。

代码执行过程：

初始化：
- result = [0, 0, 0, 0, 0, 0, 0, 0]
- stack = []
遍历温度数组：
- i = 0，temperatures[0] = 73：
  - stack = [0]
- i = 1，temperatures[1] = 74：
  - temperatures[1] > temperatures[0]，pre = 0，result[0] = 1，stack.pop()，stack = [1]
- i = 2，temperatures[2] = 75：
  - temperatures[2] > temperatures[1]，pre = 1，result[1] = 1，stack.pop()，stack = [2]
- i = 3，temperatures[3] = 71：
  - stack = [2, 3]
- i = 4，temperatures[4] = 69：
  - stack = [2, 3, 4]
- i = 5，temperatures[5] = 72：
  - temperatures[5] > temperatures[4]，pre = 4，result[4] = 1，stack.pop()
  - temperatures[5] > temperatures[3]，pre = 3，result[3] = 2，stack.pop()
  - stack = [2, 5]
- i = 6，temperatures[6] = 76：
  - temperatures[6] > temperatures[5]，pre = 5，result[5] = 1，stack.pop()
  - temperatures[6] > temperatures[2]，pre = 2，result[2] = 4，stack.pop()
  - stack = [6]
- i = 7，temperatures[7] = 73：
  - stack = [6, 7]
最终结果：
- result = [1, 1, 4, 2, 1, 1, 0, 0]

七、总结

单调栈的作用：
- 单调栈用于处理数组中的顺序问题，特别是找到下一个更大或更小的元素。
栈的维护：
- 栈用于存储温度的索引。
- 当前温度大于栈顶索引对应的温度时，弹出栈顶索引，并计算索引差值。
结果数组的初始化：
- 结果数组 result 的大小与 temperatures 相同，所有元素初始化为 0。
算法复杂度：
- 时间复杂度：O(n)，每个元素最多被压入和弹出栈一次。
- 空间复杂度：O(n)，用于存储结果数组和栈。