2025-08-08：重新安排会议得到最多空余时间Ⅰ。用go语言，你有一个整数 eventTime，表示整个活动从时间 0 开始，到时间 eventTime 结

2025-08-08：重新安排会议得到最多空余时间Ⅰ。用go语言，你有一个整数 eventTime，表示整个活动从时间 0 开始，到时间 eventTime 结束的总时长。

同时，你有两个等长数组 startTime 和 endTime，表示这期间有 n 个不重叠的会议，每个会议 i 的时间区间是 $startTime\[i$ , endTime $i$ ]。

你可以对最多 k 个会议进行时间上的调整。调整的方法是整体平移会议时间段，但不改变会议长度。你的目标是通过合理移动这几个会议，最大化任意两个相邻会议之间的最长连续空闲时间。

调整时需要满足：

1.会议的新顺序和原有顺序一致；

2.会议时间段依然互不重叠；

3.会议时间不能超出整个活动时间区间 $0, eventTime$ 。

请你计算并返回，在重新安排后，能够达到的最大连续空闲时间。

1 <= eventTime <= 1000000000。

n == startTime.length == endTime.length。

2 <= n <= 100000。

1 <= k <= n。

0 <= startTime $i$ < endTime $i$ <= eventTime。

endTime $i$ <= startTime $i + 1$ 其中 i 在范围 $0, n - 2$ 之间。

输入：eventTime = 10, k = 1, startTime = $0,2,9$ , endTime = $1,4,10$ 。

输出：6。

解释：

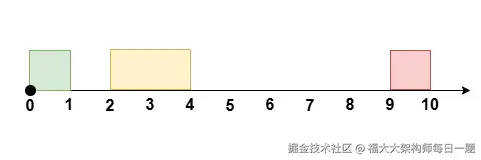
将 $2, 4$ 的会议安排到 $1, 3$ ，得到空余时间 $3, 9$ 。

题目来自力扣3439。

示例分析

给定的示例是：

eventTime = 10
k = 1
startTime = [0, 2, 9]
endTime = [1, 4, 10]

初始的会议时间区间是：

会议 0: $0, 1$
会议 1: $2, 4$
会议 2: $9, 10$

初始的空闲时间是：

会议 0 和会议 1 之间：1 (即 1 到 2)
会议 1 和会议 2 之间：5 (即 4 到 9)
会议 2 之后：0 (因为活动已经结束)

最大空闲时间是 5。

现在可以调整最多 k = 1 个会议。调整会议 1 $2, 4$ 到 $1, 3$ ：

会议 0: $0, 1$
会议 1: $1, 3$ (调整后)
会议 2: $9, 10$

新的空闲时间是：

会议 0 和会议 1 之间：0 (因为 1 到 1)
会议 1 和会议 2 之间：6 (即 3 到 9)
会议 2 之后：0

最大空闲时间是 6，因此输出 6。

解题思路

我们需要找到一种方法，通过调整最多 k 个会议的位置，使得相邻会议之间的空闲时间最大化。关键在于如何高效地计算调整后的空闲时间。

关键观察

空闲时间的定义 ：相邻会议之间的空闲时间是 startTime[i+1] - endTime[i]。我们需要最大化这些值中的最小值（或者直接找到最大的空闲时间）。
调整会议的影响 ：调整一个会议的位置会影响其与前一个会议和后一个会议的空闲时间。具体来说：
- 如果将会议 i 向左移动（即提前），那么 startTime[i] 会减小，endTime[i] 也会减小相同的量（因为会议长度不变）。这会：
  - 增加 startTime[i] - endTime[i-1]（与前一个会议的空闲时间）
  - 减少 startTime[i+1] - endTime[i]（与后一个会议的空闲时间）
- 向右移动则相反。
滑动窗口 ：我们可以考虑滑动窗口的方式，计算在调整窗口内的会议时，能够获得的最大空闲时间。具体来说：
- 对于每个可能的窗口（即连续的 k 个会议），计算调整这些会议后能够获得的最大空闲时间。
- 调整窗口内的会议时，需要确保：
  - 会议顺序不变；
  - 会议不重叠；
  - 会议不超出 [0, eventTime]。

具体步骤

初始空闲时间计算：首先计算初始的所有相邻会议之间的空闲时间。
滑动窗口处理 ：
- 对于每个可能的窗口（即连续的 k 个会议），尝试将这些会议向左或向右移动，以增加某个空闲时间。
- 具体来说，可以尝试将窗口内的会议尽可能向左移动（即尽可能提前），以增加窗口右侧的空闲时间；或者尽可能向右移动（即尽可能推迟），以增加窗口左侧的空闲时间。
- 移动时需要确保不违反约束条件（不重叠、不超出边界）。
更新最大空闲时间：在每次调整后，计算新的空闲时间，并更新最大值。

示例的详细步骤

以示例为例：初始会议：

会议 0: $0, 1$
会议 1: $2, 4$
会议 2: $9, 10$

空闲时间：

空闲 0: 1 (1-0)
空闲 1: 5 (9-4)
空闲 2: 0 (10-10)

调整 k=1 个会议：

调整会议 0：
- 不能向左移动（已经是最左）。
- 向右移动：可以移动到 $1, 2$ ，但这样会议 1 需要移动到 $2, 4$ 之后（可能需要调整会议 1），比较复杂。
调整会议 1：
- 向左移动：可以移动到 1, 3（因为会议 0 的 endTime 是 1，不能重叠）。
  - 新的空闲时间：
    - 空闲 0: 0 (1-1)
    - 空闲 1: 6 (9-3)
    - 空闲 2: 0
  - 最大空闲时间：6
- 向右移动：可以移动到 $3, 5$ ，但这样会议 2 需要移动到 $5, 6$ 或更后（可能需要调整会议 2），比较复杂。
调整会议 2：
- 不能向右移动（已经是最右）。
- 向左移动：可以移动到 8, 9，但这样空闲时间是：
  - 空闲 0: 1
  - 空闲 1: 4 (8-4)
  - 空闲 2: 1 (10-9)
  - 最大空闲时间：4
- 不如调整会议 1 得到的 6 大。

因此，最佳调整是移动会议 1 到 $1, 3$ ，得到最大空闲时间 6。

算法复杂度

时间复杂度

初始空闲时间计算：O(n)，因为需要遍历所有会议。
滑动窗口处理：
- 对于每个窗口（共 O(n) 个窗口），计算调整后的空闲时间是 O(1)（因为只需要计算窗口前后的空闲时间）。
- 因此，滑动窗口部分的时间复杂度是 O(n)。
总体时间复杂度：O(n)。

空间复杂度

需要存储初始的空闲时间：O(n)。
其他临时变量：O(1)。
总体空间复杂度：O(n)（如果存储所有空闲时间）或 O(1)（如果即时计算）。

在给定的代码中，没有显式存储所有空闲时间，而是即时计算和比较，因此额外空间复杂度是 O(1)。

代码逻辑简述

初始化 res 为 0，t 为 0（t 表示当前窗口内会议的总长度）。
遍历所有会议（i 从 0 到 n-1）：
- 将当前会议的长度加入 t。
- 计算窗口的左边界 left：
  - 如果 i <= k-1，left 是 0（窗口从最左边开始）。
  - 否则，left 是 endTime[i-k]（窗口的左边是第 i-k 个会议的结束时间）。
- 计算窗口的右边界 right：
  - 如果 i == n-1，right 是 eventTime（窗口到最右边）。
  - 否则，right 是 startTime[i+1]（窗口的右边是第 i+1 个会议的开始时间）。
- 计算当前窗口调整后的空闲时间 right - left - t，并更新 res。
- 如果 i >= k-1，从 t 中减去最早加入的会议的长度（滑动窗口的左移）。
返回 res。

示例的代码执行

以示例为例：

eventTime = 10, k = 1, startTime = [0, 2, 9], endTime = [1, 4, 10]。
n = 3。
初始化 res = 0, t = 0。

遍历：

i = 0：
- t += 1 - 0 = 1。
- left = 0（因为 i <= 0）。
- right = startTime[1] = 2。
- right - left - t = 2 - 0 - 1 = 1。
- res = max(0, 1) = 1。
- i >= 0，t -= endTime[0] - startTime[0] = 1，t = 0。
i = 1：
- t += 4 - 2 = 2。
- left = endTime[0] = 1（因为 i > 0）。
- right = startTime[2] = 9。
- right - left - t = 9 - 1 - 2 = 6。
- res = max(1, 6) = 6。
- i >= 0，t -= endTime[1] - startTime[1] = 2，t = 0。
i = 2：
- t += 10 - 9 = 1。
- left = endTime[1] = 4。
- right = eventTime = 10。
- right - left - t = 10 - 4 - 1 = 5。
- res = max(6, 5) = 6。
- i >= 0，t -= endTime[2] - startTime[2] = 1，t = 0。

返回 res = 6。

总结

过程：通过滑动窗口的方式，计算调整窗口内 k 个会议后能够获得的最大空闲时间。每次调整时，窗口的左右边界由未调整的会议决定，窗口内的会议可以自由移动（不改变顺序、不重叠、不超出边界）。
时间复杂度 ：O(n)，因为每个会议只被处理常数次。
空间复杂度 ：O(1)，因为只使用了常数个额外变量。

Go完整代码如下：

go 复制代码

package main

import (
	"fmt"
)

func maxFreeTime(eventTime int, k int, startTime []int, endTime []int) int {
	n := len(startTime)
	res := 0
	t := 0
	for i := 0; i < n; i++ {
		t += endTime[i] - startTime[i]
		var left int
		if i <= k-1 {
			left = 0
		} else {
			left = endTime[i-k]
		}
		var right int
		if i == n-1 {
			right = eventTime
		} else {
			right = startTime[i+1]
		}
		if right-left-t > res {
			res = right - left - t
		}
		if i >= k-1 {
			t -= endTime[i-k+1] - startTime[i-k+1]
		}
	}
	return res
}

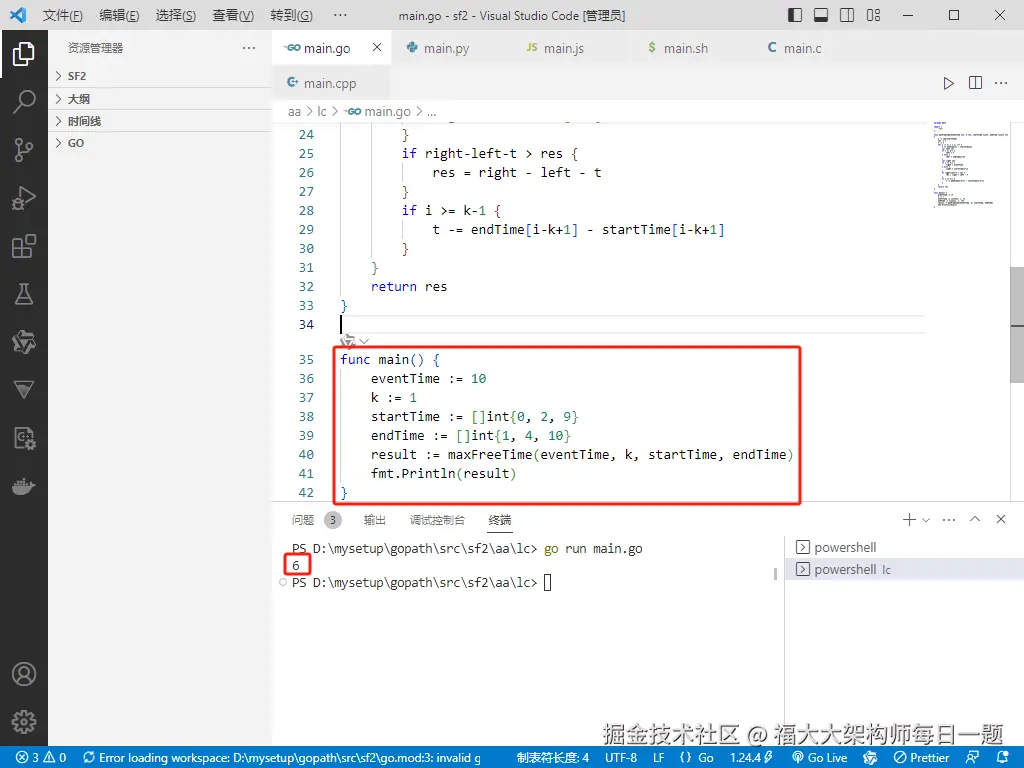
func main() {
	eventTime := 10
	k := 1
	startTime := []int{0, 2, 9}
	endTime := []int{1, 4, 10}
	result := maxFreeTime(eventTime, k, startTime, endTime)
	fmt.Println(result)
}

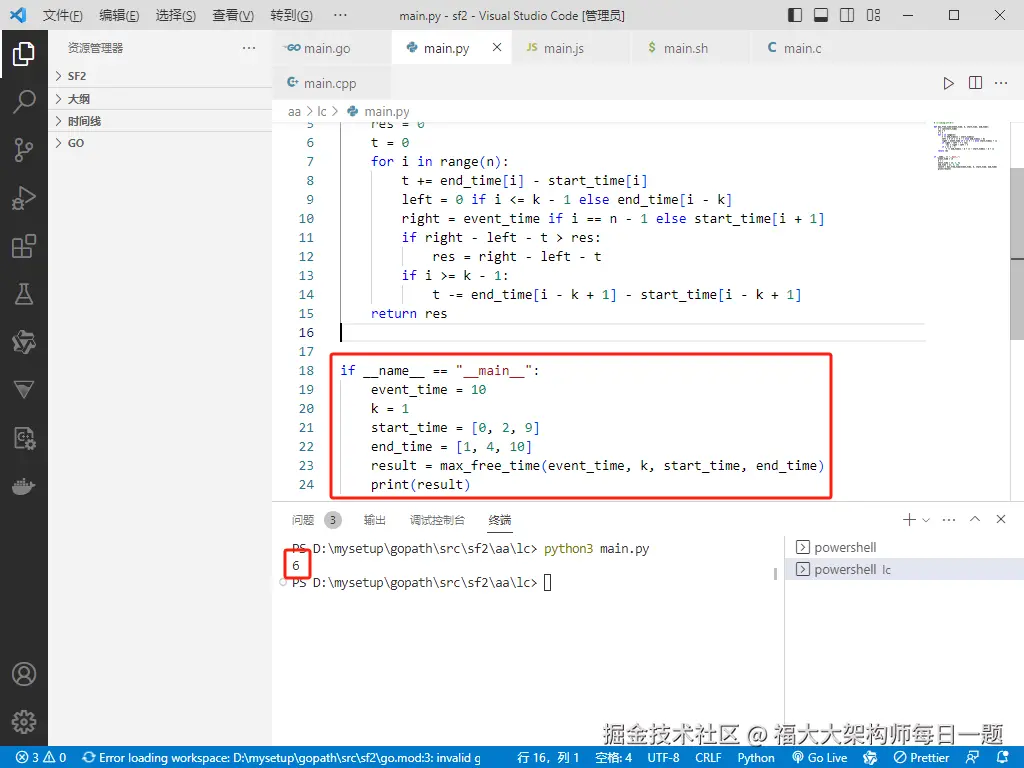
Python完整代码如下：

python 复制代码

# -*-coding:utf-8-*-

def max_free_time(event_time, k, start_time, end_time):
    n = len(start_time)
    res = 0
    t = 0
    for i in range(n):
        t += end_time[i] - start_time[i]
        left = 0 if i <= k - 1 else end_time[i - k]
        right = event_time if i == n - 1 else start_time[i + 1]
        if right - left - t > res:
            res = right - left - t
        if i >= k - 1:
            t -= end_time[i - k + 1] - start_time[i - k + 1]
    return res


if __name__ == "__main__":
    event_time = 10
    k = 1
    start_time = [0, 2, 9]
    end_time = [1, 4, 10]
    result = max_free_time(event_time, k, start_time, end_time)
    print(result)