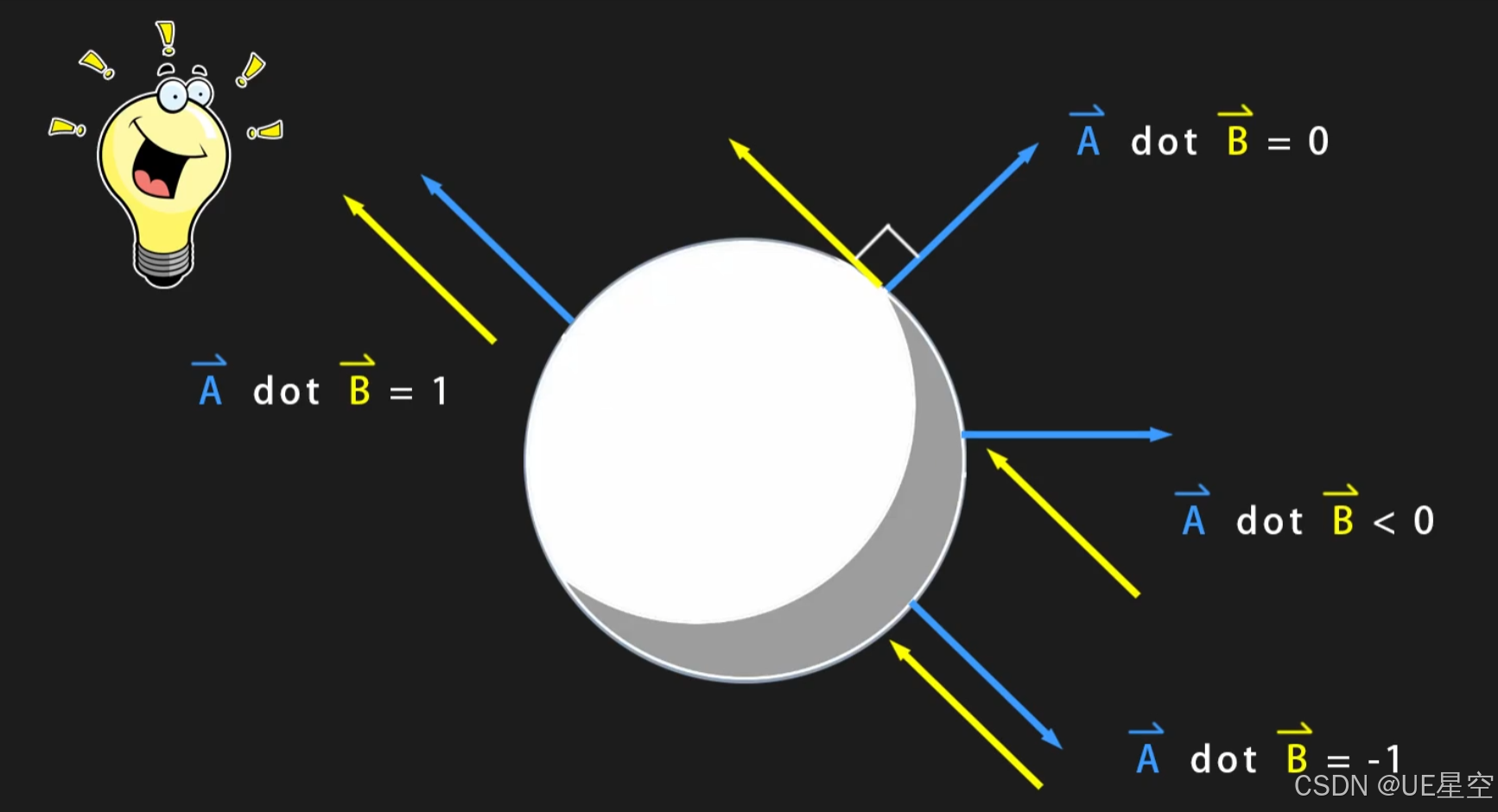
Dot通常指的是"点积"(Dot Product),是向量运算中的一种基本操作。它用于计算两个向量的相似性或者投影。在材质中,点积常用于以下几种情况:
-
法线与视角的关系:点积常用于计算光照效果。例如,计算表面法线与光源方向的点积可以帮助确定表面与光线的角度,从而影响光照强度。这通常应用于漫反射、镜面反射等计算中。
-
计算角度:通过计算两个向量的点积,可以得到它们之间的夹角。比如计算视线与法线的角度,用于实现更真实的光照和反射效果。
在材质编辑器中,点积操作通过 Dot 节点来实现,你可以将两个向量输入到该节点,输出一个标量值,表示它们之间的点积结果。
点积公式是:
Dot(A,B)=∣A∣⋅∣B∣⋅cos(θ)\text{Dot}(A, B) = |A| \cdot |B| \cdot \cos(\theta)Dot(A,B)=∣A∣⋅∣B∣⋅cos(θ)
其中:
-
AAA 和 BBB 是两个向量
-
∣A∣|A|∣A∣ 和 ∣B∣|B|∣B∣ 是向量的模长
-
θ\thetaθ 是两个向量之间的夹角
这个结果通常被用于计算光照、反射、阴影或任何依赖角度差异的效果。
参考链接: