
- 多源BFS简介
- [一、[01 矩阵](https://leetcode.cn/problems/01-matrix/description/)](#一、01 矩阵)
- 二、[飞地的数量](https://leetcode.cn/problems/number-of-enclaves/description/)
- 三、[地图中的最高点](https://leetcode.cn/problems/map-of-highest-peak/description/)
- 四、[地图分析](https://leetcode.cn/problems/as-far-from-land-as-possible/description/)
- 结尾
多源BFS简介
多源 BFS 是广度优先搜索(BFS)的一种扩展形式,核心思想是从多个初始节点同时出发,按照层次逐层向外扩展,适用于需要计算 "多个源点到其他节点的最短距离" 或 "全局最优解" 的场景。
在单权(即所有边的权重相同,通常为 1)的情况下,多源 BFS 的优势尤为明显,因为 BFS 的 "逐层扩展" 特性天然保证了首次到达某节点时的距离就是最短距离。
一、01 矩阵
题目描述:

思路讲解:
本道题需要我们计算矩阵中每个 非0 到最近的 0 的距离,若正向搜索从 非0 到 0 的最近距离,需要我们找到最近 0 ,然后倒回去修改 非0 上的距离,这样会显得很麻烦,所以我们可以换一种思路,找到所有的 0 ,然后同时向外逐层扩展搜索,找到最近的 非0,并修改它的距离。以下是具体思路:
-
将所有值为 0 的位置作为 BFS 的起点(初始队列),因为它们到自身的距离为 0。创建与原矩阵同等规模的矩阵 ans,初始化距离矩阵 ans,其中值为 0 的位置距离为 0,其余位置初始化为-1(表示尚未访问)
-
定义一个变量记录当前距离
-
BFS逐层扩展搜索:
- 记录当前队列中元素的个数为 cnt,并将距离 +1
- 将以下步骤循环执行 cnt 次
- 从队列中取出当前位置,遍历其上下左右四个相邻位置
- 若相邻位置未被访问过,则更新其距离为当前距离 + 1,并将其加入队列
-
队列为空时,所有位置的最短距离均已计算完毕
编写代码:
cpp
class Solution {
int dx[4] = {0,0,-1,1};
int dy[4] = {1,-1,0,0};
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
int rows = mat.size() , cols = mat[0].size();
vector<vector<int>> ans(rows,vector<int>(cols,-1));
queue<pair<int,int>> qu;
for(int i = 0 ; i < rows ; i++)
{
for(int j = 0 ; j < cols ; j++)
{
if(mat[i][j] == 0)
{
qu.push({i,j});
ans[i][j] = 0;
}
}
}
while(!qu.empty())
{
int qu_x = qu.front().first , qu_y = qu.front().second;
qu.pop();
for(int i = 0 ; i < 4 ; i++)
{
int x = qu_x + dx[i] , y = qu_y + dy[i];
if(x >= 0 && x < rows && y >= 0 && y < cols && mat[x][y] != 0 && ans[x][y] == -1)
{
qu.push({x,y});
ans[x][y] = ans[qu_x][qu_y] + 1;
}
}
}
return ans;
}
};二、飞地的数量
题目描述:
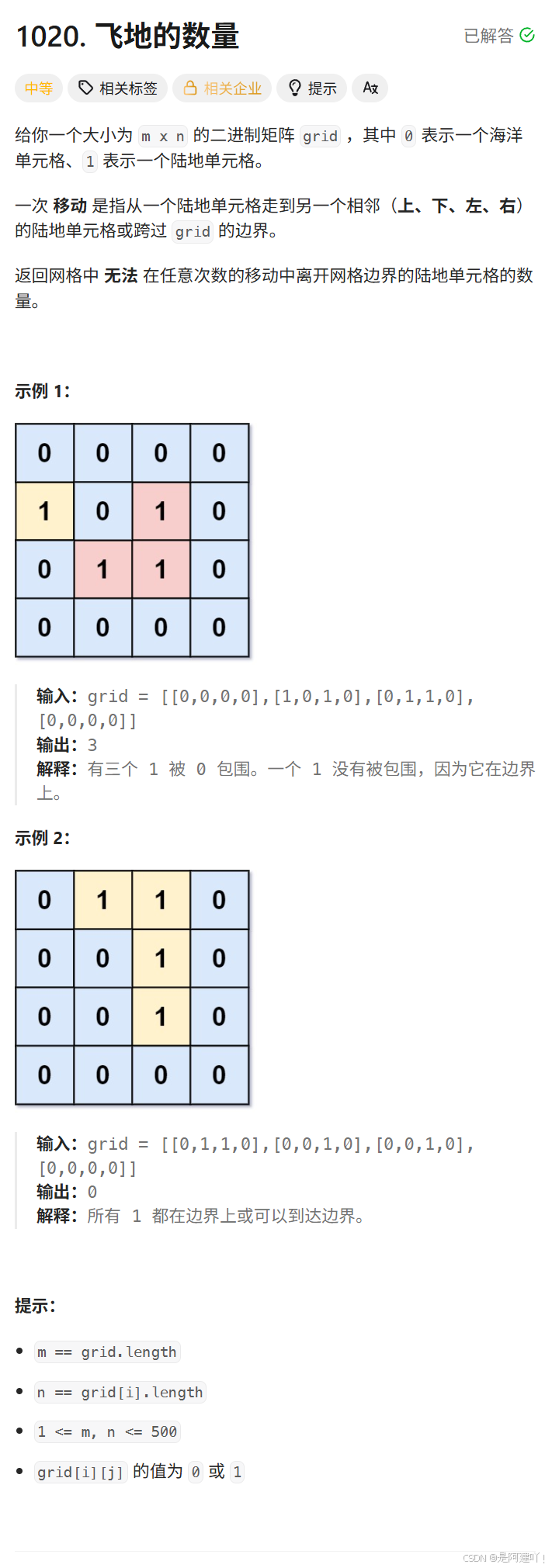
思路讲解:
本道题需要我们找到所有无法通过移动到达网格边界的陆地单元格(即被海洋完全包围的陆地)。但是想要正向判断是否无法通过移动到达网格边界的陆地单元格,需要先找到一个未被访问的陆地单元格,再通过一次BFS判断该区域是否被海洋包围,如果被海洋包围,则增加陆地单元格的数量。
这里还有一种方式我认为比上面一个方法更加简单。先找出所有不被围绕的陆地,并将这些陆地标记为已访问,剩下的陆地都是不被包围的,再遍历整个二维数组,记录剩下陆地的数量。
- 遍历二维数组中边缘四条边中的每个位置 [i, j] ,将所有陆地单元格的位置作为 BFS 的起点
- 创建与原矩阵同等规模的矩阵 vis,初始化距离矩阵 vis 为 false,表示尚未访问
- BFS 处理连通区域:
- 记录当前队列中元素的个数为 cnt
- 将以下步骤循环执行 cnt 次
- 从队列中取出位置,遍历其上下左右四个方向的相邻位置
- 对每个相邻位置,若在二维数组范围内且为陆地,将该位置标记为false,表示已访问,继续扩展处理
- 遍历二维数组,统计未被访问并且为陆地的数量
- 处理完毕后,返回陆地数量
编写代码:
cpp
class Solution {
int dx[4] = {0, 0, -1, 1};
int dy[4] = {1, -1, 0, 0};
public:
int numEnclaves(vector<vector<int>>& grid) {
int rows = grid.size(), cols = grid[0].size();
vector<vector<bool>> vis(rows, vector<bool>(cols, false));
queue<pair<int, int>> qu;
for (int i = 0; i < rows; i++)
{
if (grid[i][0] == 1)
{
qu.push({i, 0});
vis[i][0] = true;
}
if (grid[i][cols - 1] == 1)
{
qu.push({i, cols - 1});
vis[i][cols - 1] = true;
}
}
for (int i = 0; i < cols; i++)
{
if (grid[0][i] == 1)
{
qu.push({0, i});
vis[0][i] = true;
}
if (grid[rows - 1][i] == 1)
{
qu.push({rows - 1, i});
vis[rows - 1][i] = true;
}
}
while (!qu.empty())
{
int qu_x = qu.front().first, qu_y = qu.front().second;
qu.pop();
for (int i = 0; i < 4; i++)
{
int x = qu_x + dx[i], y = qu_y + dy[i];
if (x >= 0 && x < rows && y >= 0 && y < cols &&
grid[x][y] == 1 && vis[x][y] == false)
{
qu.push({x, y});
vis[x][y] = true;
}
}
}
int ans = 0;
for (int i = 1; i < rows - 1; i++)
{
for (int j = 1; j < cols - 1; j++)
{
if (grid[i][j] == 1 && vis[i][j] == false)
ans++;
}
}
return ans;
}
};三、地图中的最高点
题目描述:
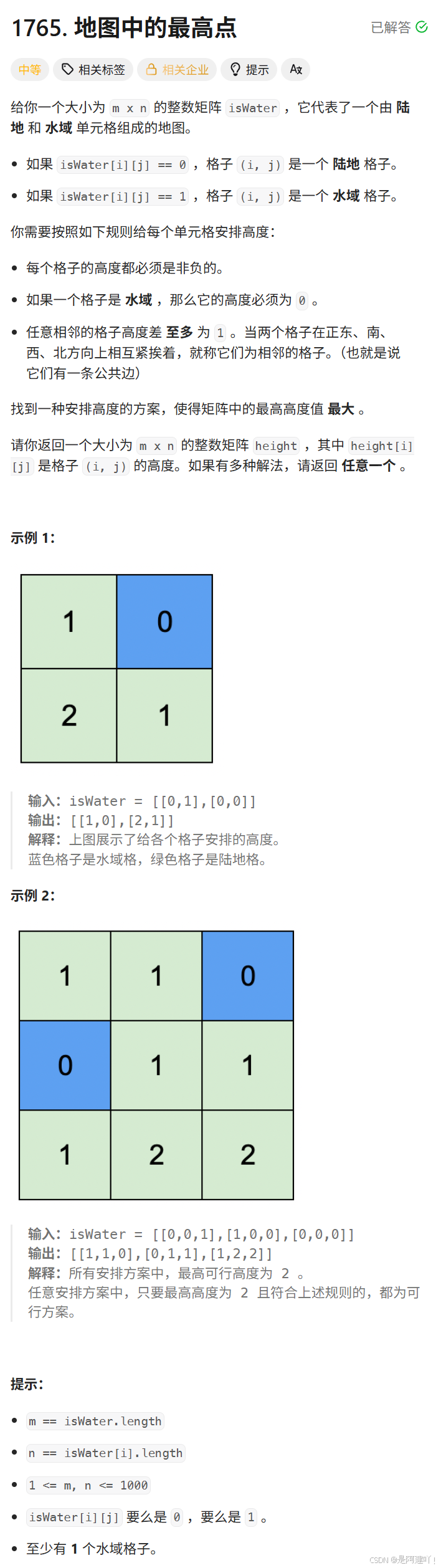
思路讲解:
本道题需要我们为每个单元格分配高度,使得水域单元格高度为 0,相邻单元格高度差不超过 1,并且最高高度尽可能大。通过使用BFS从所有水域单元格同步向外扩展,可以确保每个陆地单元格的高度是到最近水域的最短距离。以下是具体思路:
- 将所有水域单元格(值为 1 的位置)加入 BFS 队列。创建与原二维数组同等规模的二维数组 ans,初始化二维数组 ans 高度,其中水域位置高度为 0,陆地位置初始为 - 1(表示未访问)
- 定义一个变量记录当前高度
- BFS逐层扩展搜索:
- 记录当前队列中元素的个数为 cnt,并将高度 +1
- 将以下步骤循环执行 cnt 次
- 从队列中取出当前位置,遍历其上下左右四个相邻位置
- 若相邻位置为未访问的陆地,则将其高度设为当前高度,并加入队列继续扩展
- 所有单元格的高度均已计算完毕,返回二维数组ans
编写代码:
cpp
class Solution {
int dx[4] = {0, 0, -1, 1};
int dy[4] = {1, -1, 0, 0};
public:
vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {
int rows = isWater.size() , cols = isWater[0].size();
vector<vector<int>> ans(rows,vector<int>(cols,-1));
queue<pair<int,int>> qu;
for(int i = 0 ; i < rows ; i++)
{
for(int j = 0 ; j < cols ; j++)
{
if(isWater[i][j] == 1)
{
ans[i][j] = 0;
qu.push({i,j});
}
}
}
while(!qu.empty())
{
int qu_x = qu.front().first , qu_y = qu.front().second;
qu.pop();
for(int i = 0 ; i < 4 ; i++)
{
int x = qu_x + dx[i] , y = qu_y + dy[i];
if(x >= 0 && x < rows && y >= 0 && y < cols && isWater[x][y] == 0 && ans[x][y] == -1)
{
qu.push({x,y});
ans[x][y] = ans[qu_x][qu_y] + 1;
}
}
}
return ans;
}
};四、地图分析
题目描述:

思路讲解:
本道题需要我们找到距离最近陆地最远的海洋单元格,并返回其曼哈顿距离。假设"从海洋找陆地",两个相邻的海洋单元格可能会重复搜索同一区域的陆地,会导致重复计算和高时间复杂度。
这里我们换一种思路"从陆地找海洋",通过从所有陆地单元格同步向外扩展,可以逐层计算每个海洋单元格到最近陆地的距离,最后取最大值即可。
- 将所有陆地单元格(值为 1 的位置)加入 BFS 队列,初始距离为 0。初始化距离矩阵ans,陆地位置距离为 0,海洋位置初始为 - 1(表示未访问)。
- 定一个变量记录最大距离,再定义一个变量记录当前距离
- BFS逐层扩展搜索:
- 记录当前队列中元素的个数为 cnt,并将当前距离 +1
- 将以下步骤循环执行 cnt 次
- 从队列中取出当前位置,遍历其上下左右四个相邻位置
- 若相邻位置为未访问的海洋,则将其距离设为当前距离,通过与最大距离对比,得到新的最大距离
- 若相邻位置为未访问的海洋,将该位置设置为false,表示已访问,并将该位置加入队列继续扩展
- 若所有单元格都是陆地或海洋,返回 - 1,反正则返回最大距离
编写代码:
cpp
class Solution {
int dx[4] = {0, 0, -1, 1};
int dy[4] = {1, -1, 0, 0};
public:
int maxDistance(vector<vector<int>>& grid) {
int rows = grid.size() , cols = grid[0].size();
vector<vector<bool>> vis(rows,vector<bool>(cols,false));
queue<pair<int,int>> qu;
for(int i = 0 ; i < rows ; i++)
{
for(int j = 0 ; j < cols ; j++)
{
if(grid[i][j] == 1)
{
qu.push({i,j});
vis[i][j] = true;
}
}
}
int ans = -1;
while(!qu.empty())
{
ans++;
int cnt = qu.size();
while(cnt--)
{
int qu_x = qu.front().first , qu_y = qu.front().second;
qu.pop();
for(int i = 0 ; i < 4 ; i++)
{
int x = qu_x + dx[i] , y = qu_y + dy[i];
if(x >= 0&& x < rows && y >= 0 && y < cols && grid[x][y] == 0 && vis[x][y] == false)
{
qu.push({x,y});
vis[x][y] = true;
}
}
}
}
if(ans == 0) return -1;
else return ans;
}
};结尾
如果有什么建议和疑问,或是有什么错误,大家可以在评论区中提出。
希望大家以后也能和我一起进步!!🌹🌹
如果这篇文章对你有用的话,希望大家给一个三连支持一下!!🌹🌹
