一、题目解析

1、需返回排序好的第k个最大元素
2、要求时间复杂度为O(N)
二、算法原理
解法1:堆排序(大根堆) k*O(N)
借用大堆的性质,将元素插入到大堆中,按照k输出堆顶第k个元素
解法2:堆排序(小根堆) (N-k)*O(logN)
先建k个小堆,然后插入元素,依次与堆顶元素比较,比堆顶元素大,则pop(删除堆顶元素)掉堆顶元素,插入nums[i],最终小堆中存储前k个最大的数
解法3:分治-快排 O(N)
基于数组分三块+随机数选择元素
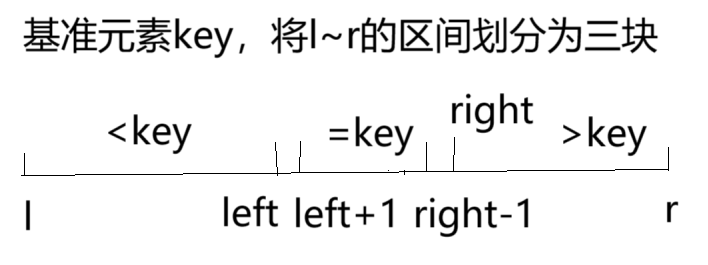
通过埋下随机数种子srand(time(NULL)),rand() % (right-left+1) + left,找到随机数下标,得到基准元素key
由i移动遍历数组,left = -1,right = nums.size()+1,如果nums[i]<key, swap(nums[i++],nums[++left]);如果nums[i] == key,i++;如果nums[i]>key,swap(nums[i],nums[--right])
依据排序好的数组,统计区间各个元素的个数判断情况

三、代码示例
解法1:
cpp
int findKthLargest(vector<int>& nums, int k)
{
sort(nums.begin(),nums.end(),greater<int>());
return nums[k-1];
// O(N)
//大堆
priority_queue<int> pq(nums.begin(),nums.end());
while(--k)
{
pq.pop();
}
return pq.top();
//K*logN
}
解法2:
cpp
int findKthLargest(vector<int>& nums, int k)
{
//小堆
//(N-K)*logN
priority_queue<int,vector<int>,greater<int>> pq(nums.begin(),nums.begin()+k);//建k个数的小堆
for(int i = k;i < nums.size();i++)
{
if(nums[i] > pq.top())
{
pq.pop();
pq.push(nums[i]);
}
}
return pq.top();
}
解法3:
cpp
int findKthLargest(vector<int>& nums, int k)
{
//快排
srand(time(NULL));
return qsort(nums,0,nums.size()-1,k);
}
int qsort(vector<int>& nums,int l,int r,int k)
{
if(l == r) return nums[l];
//随机选择基准元素
int key = getRandom(nums,l,r);
//基准元素分三块
int left = l-1,right = r+1,i = l;
while(i<right)
{
if(nums[i]<key) swap(nums[++left],nums[i++]);
else if(nums[i] == key) i++;
else swap(nums[i],nums[--right]);
}
//分情况讨论
int c = r - right +1,b = right - left - 1;
if(c>=k) return qsort(nums,right,r,k);
else if(b+c>=k) return key;
else return qsort(nums,l,left,k-b-c);
}
int getRandom(vector<int>& nums,int left,int right)
{
return nums[rand() % (right - left + 1) + left];
}