LeetCode快乐数问题

快乐数

快乐数问题

题目描述

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」定义为：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是无限循环但始终变不到 1。
如果这个过程结果为 1，那么这个数就是快乐数。
如果 n 是快乐数就返回 true ；不是，则返回 false 。

解题思想

对于该问题，首先题目明确了两种结果，一个是最终能变为1，一个则是无限循环，意思是进入了一个环路。当n=2，会发现最终进入了一个环路。

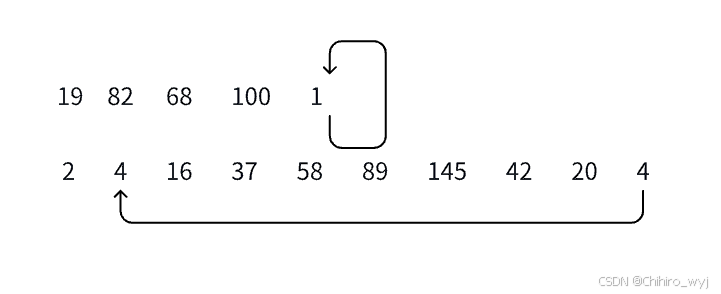
我们可以把这两种情况变为一种情况，最终都是进入环路，但实际上变为1进入的是全为1的环路，那么该问题就变为了环路中的元素是不是1。

采用快慢指针的方法，判断链表是否有环也是该方法，因为本题一定有环，如果最终快慢指针最终相遇的位置值为1，则是快乐数。快指针一次移动两步，慢指针一次移动一步，最终一定在环中相遇。本题的快慢指针实际上就是结果的值，例如slow=19，fast=82,第二次则slow变为19的下一位值，fast变为82的下下个值。Getsquare函数就是自定义的用于计算某一个数各位置平方和的函数。

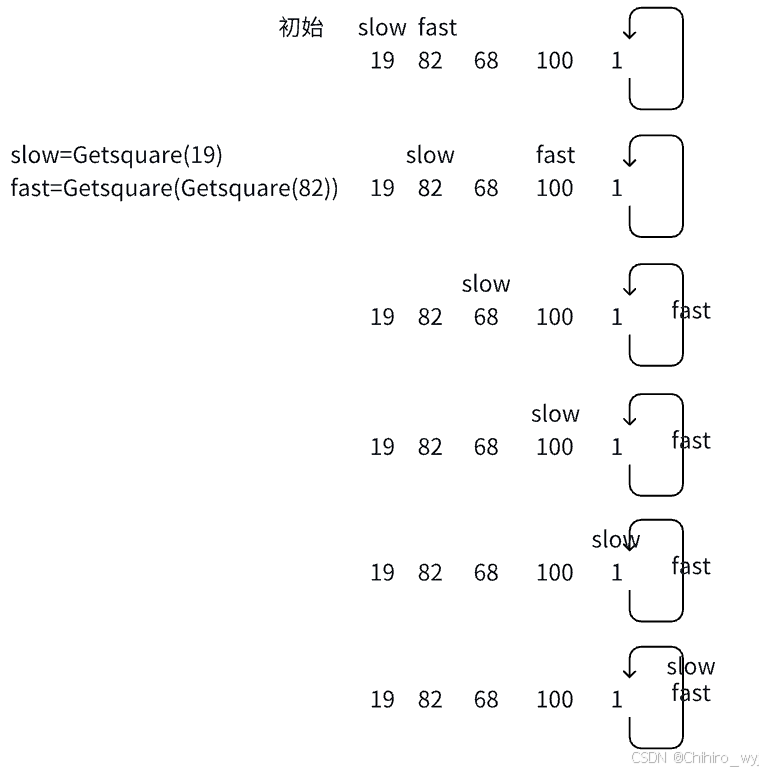
我们还可以采用鸽巢思想，即有n个巢穴，有n+1个鸽子，则必然出现有一个巢穴有多个鸽子的情况。本题范围为2^31 - 1,是10位数，那么我们可以假设他最大能达到9999999999，那么数据范围实际上就是在[1,810]之间（810=9910），共810个数，那么如果一个数据的函数调用次数超过了810，还没有出现1，就会进入循环，则永远不会出现1，说明不是快乐数。否则就是快乐数，可以结合快慢指针，这样就不会每次都循环810次。

cpp 复制代码

class Solution {
public:
//双指针
    int getSquare(int n)
    {
        int sum=0;
        while(n)
        {
            int tmp=n%10;
            sum+=tmp*tmp;
            n/=10;
        }
        return sum;
    }
    bool isHappy(int n) {
        int slow=n;
        int fast=getSuqare(n);
        while(fast!=slow)
        {
            fast=getSquare(getSquare(fast));
            slow=getSquare(slow);
        }
        if(fast==1)
        {
            return true;
        }
        return false;
    }
};

cpp 复制代码

//鸽巢+双指针
class Solution {
public:
    int getSquare(int n)
    {
        int sum=0;
        while(n)
        {
            int tmp=n%10;
            sum+=tmp*tmp;
            n/=10;
        }
        return sum;
    }
    bool isHappy(int n) 
    {
	    int slow = n, fast = n;
	    for (int i = 0; i < 810; ++i) 
	    {
	        slow = getSquare(slow);
	        fast = getSquare(getSquare(fast));
	        if (fast == 1) return true;
	        if (slow == fast) return false; // 检测到循环
	    }
	    return false; // 超过810次未到1
	}
};