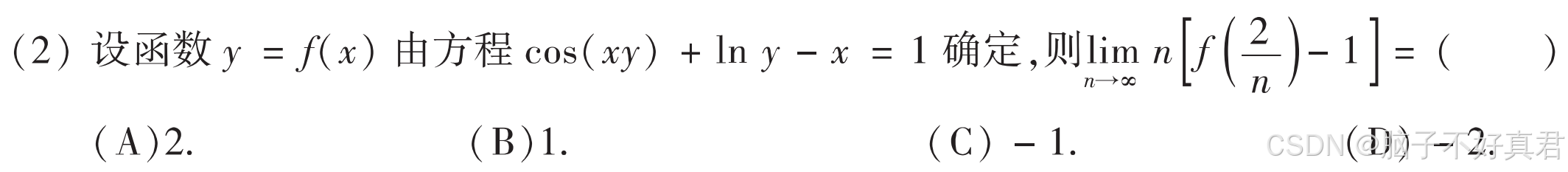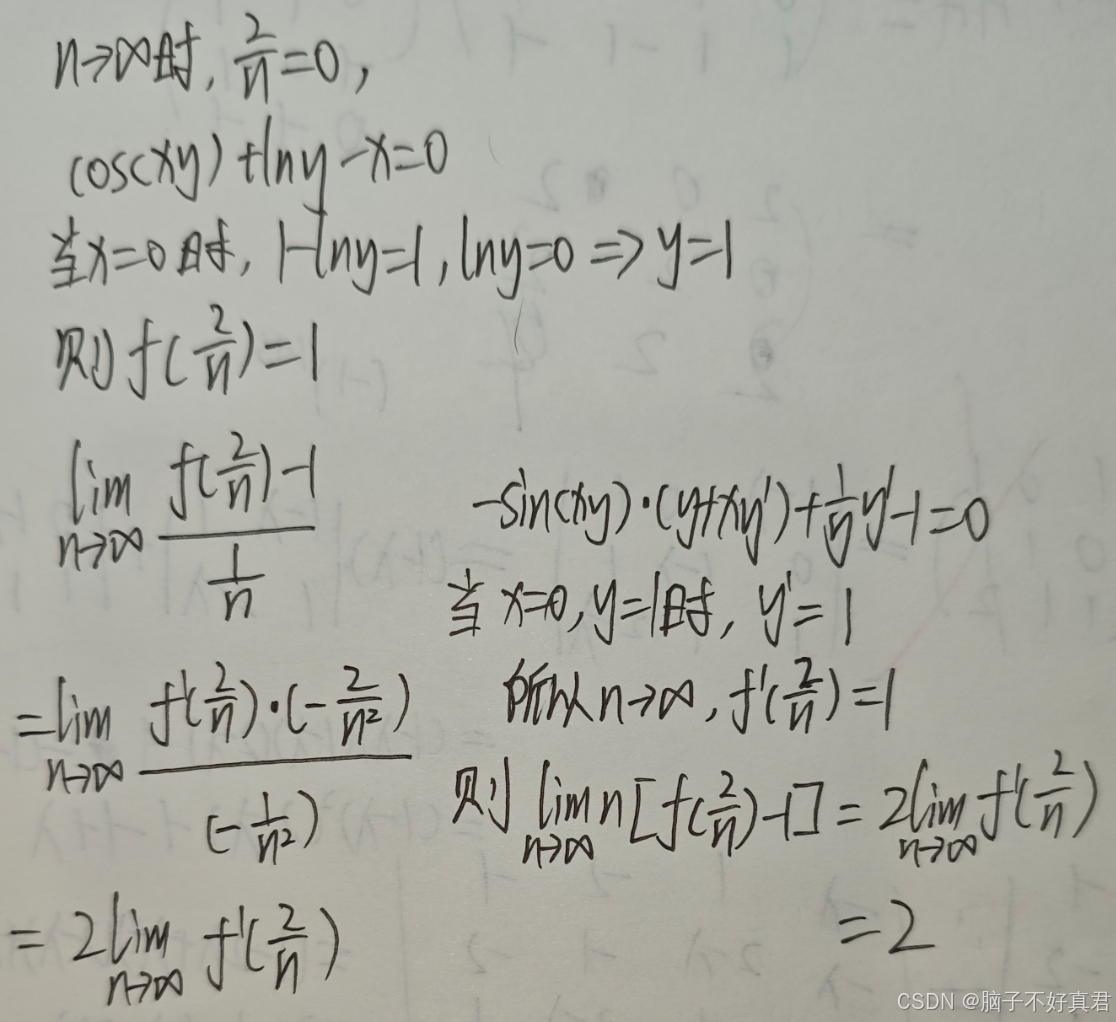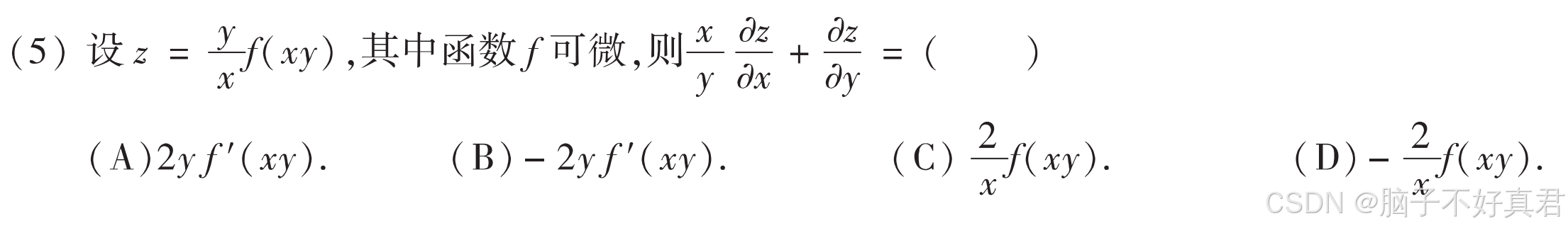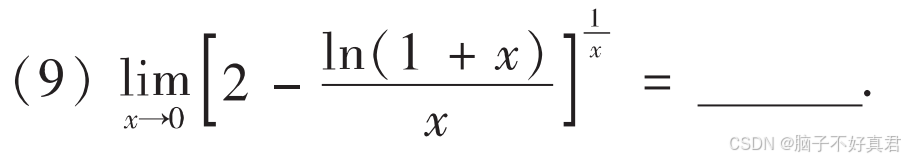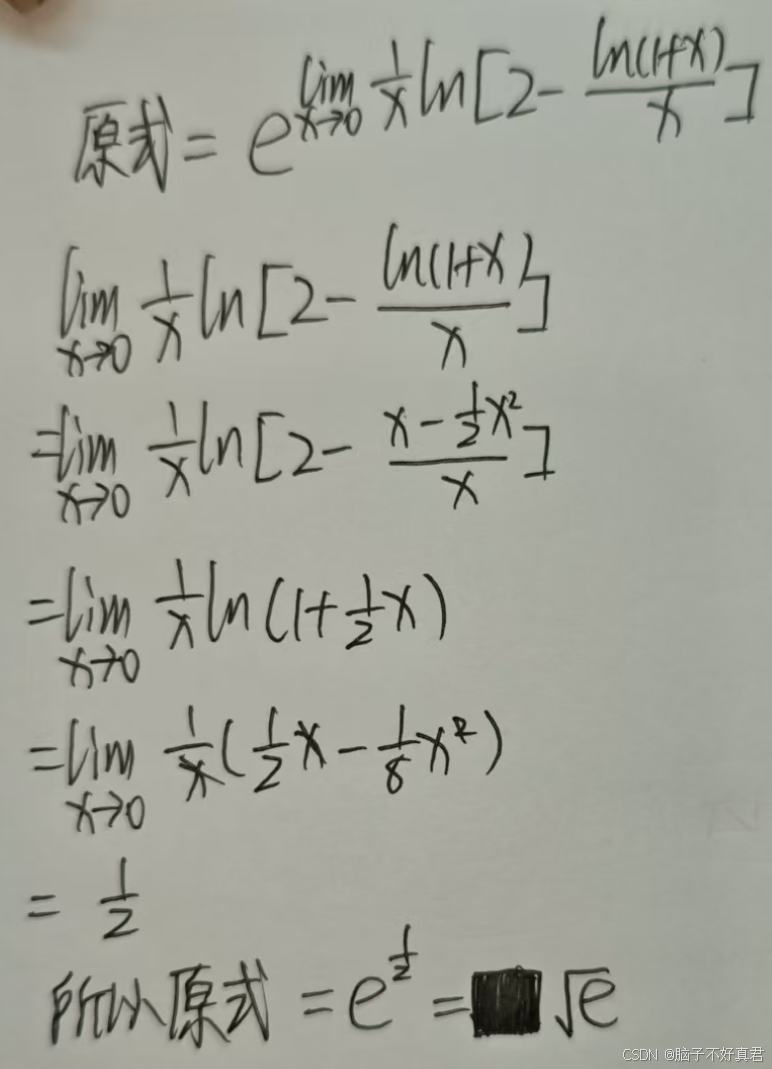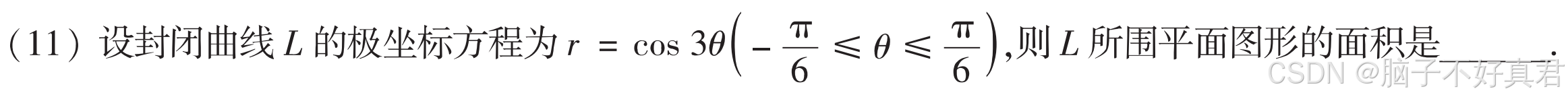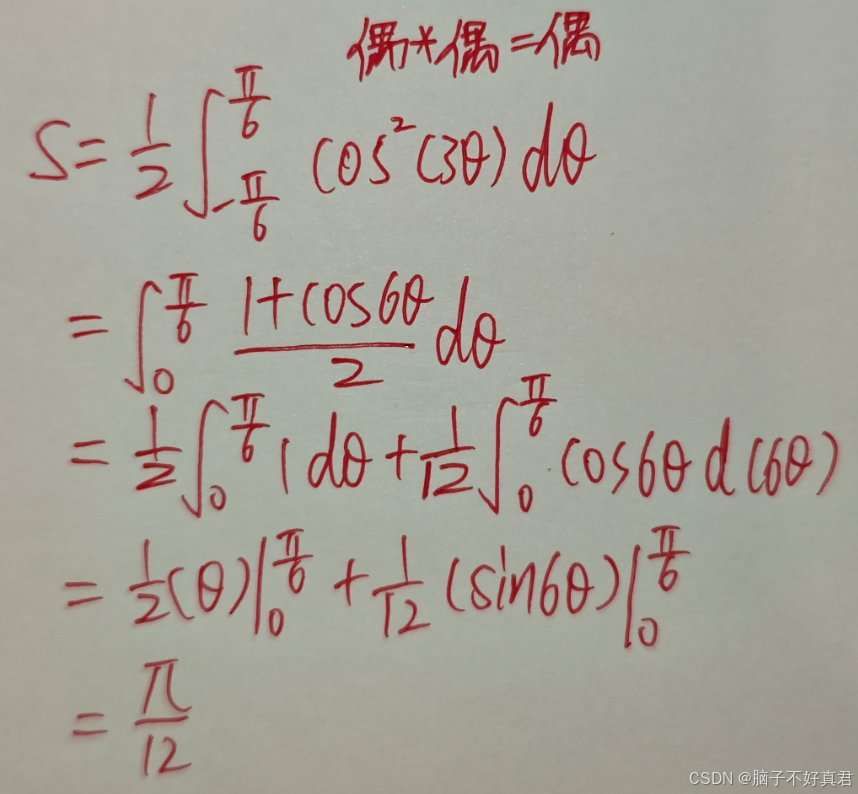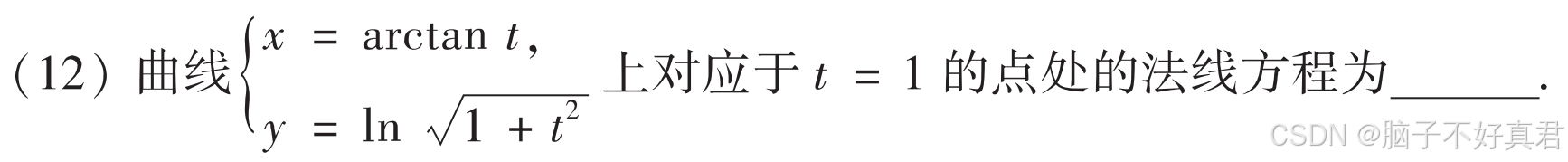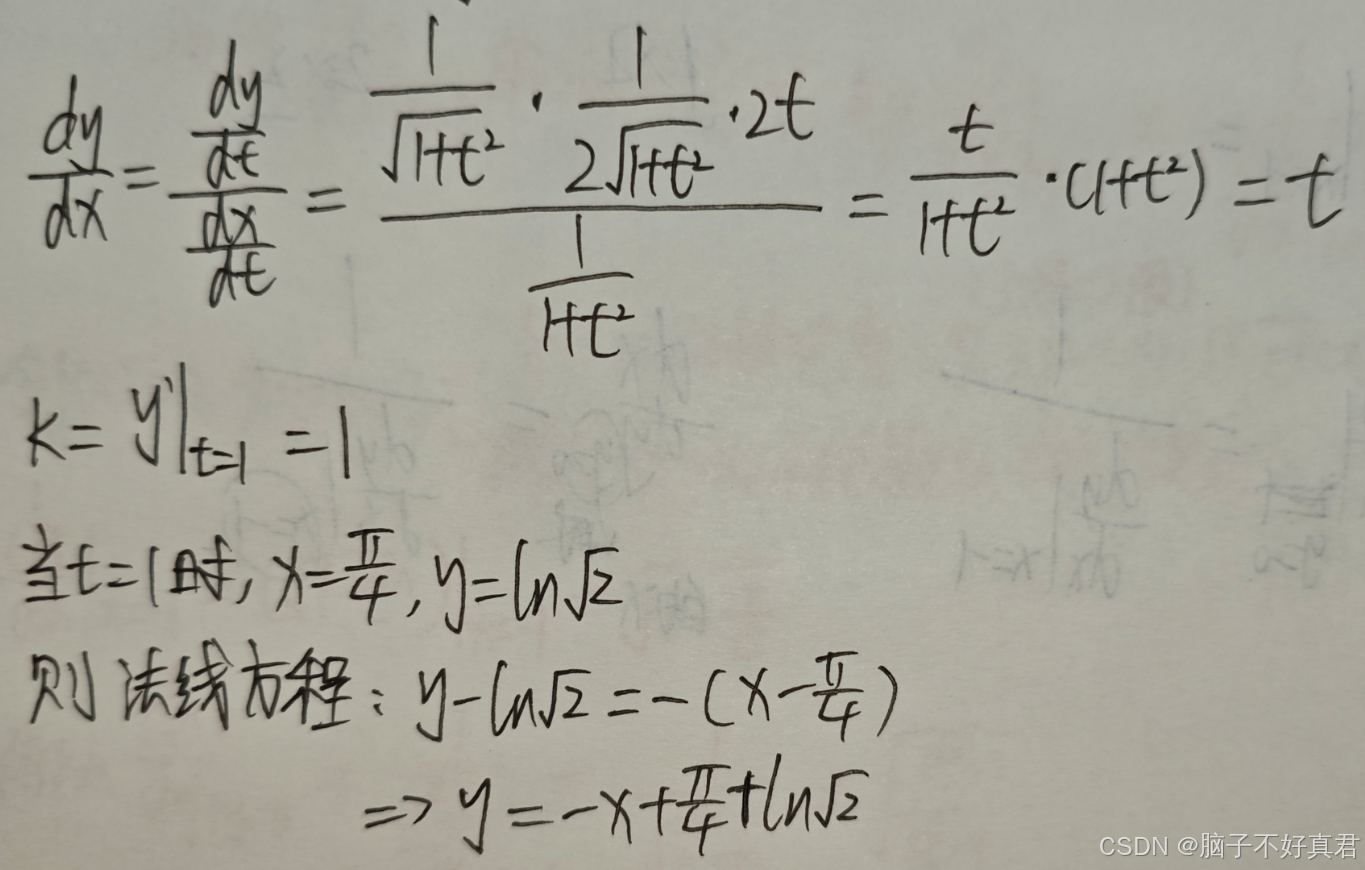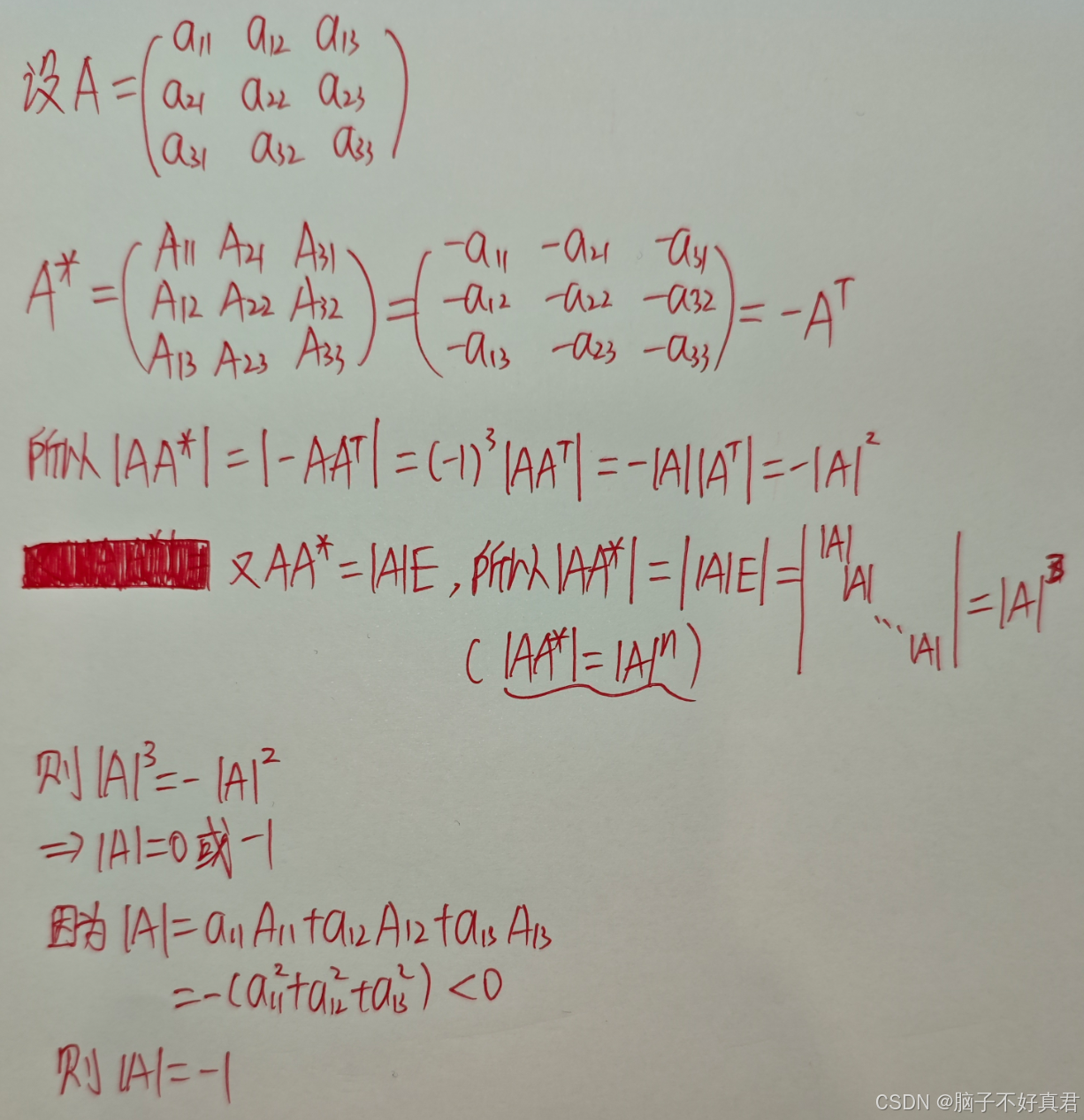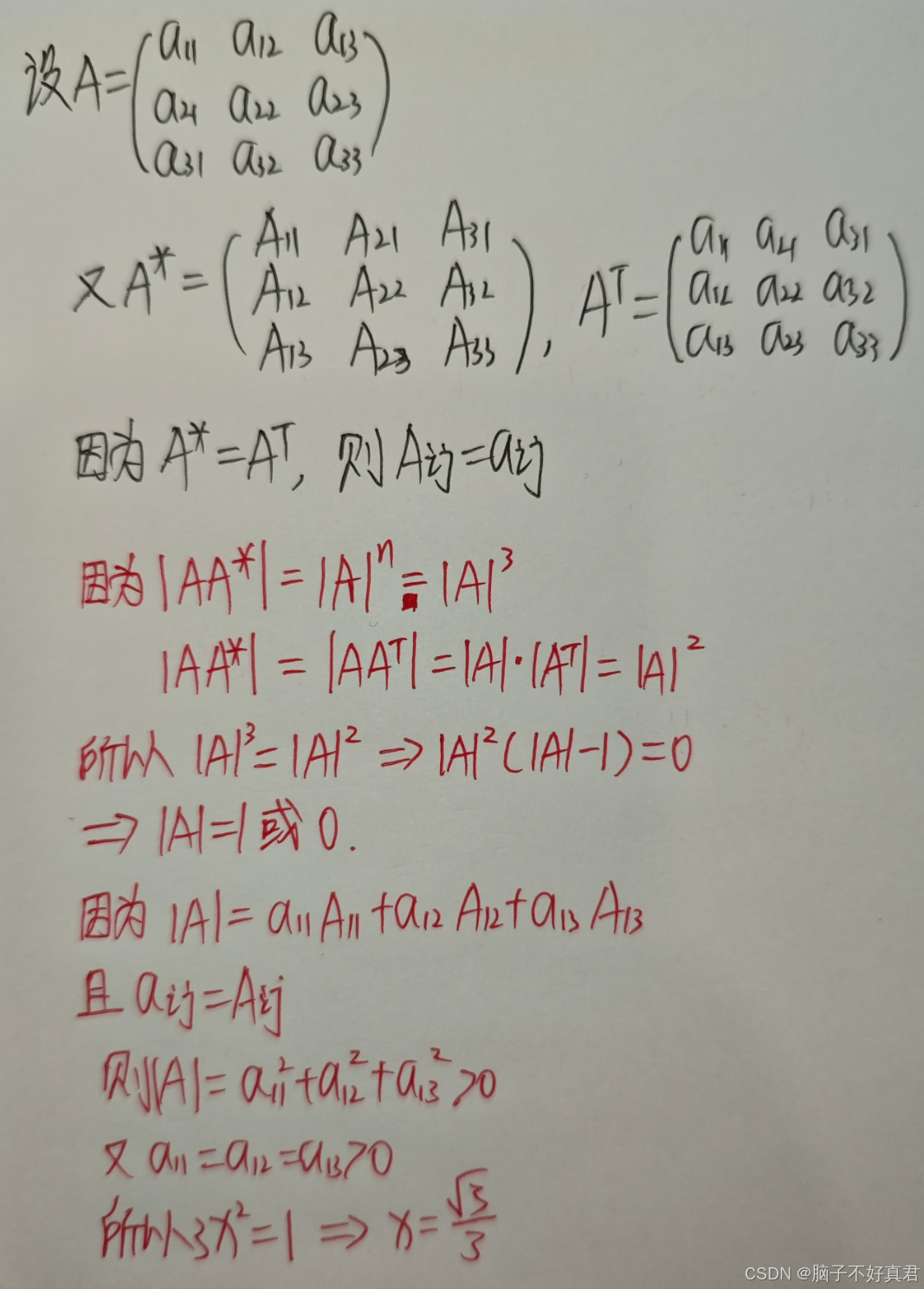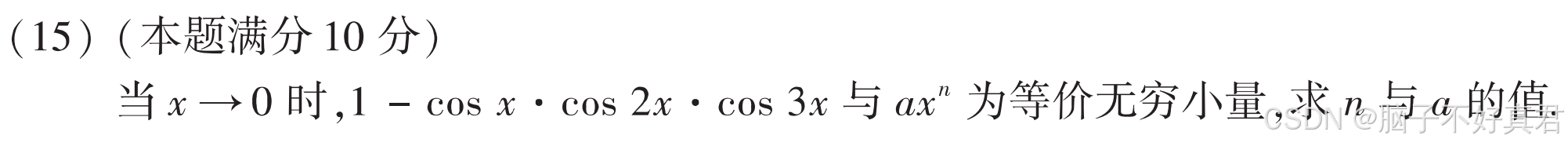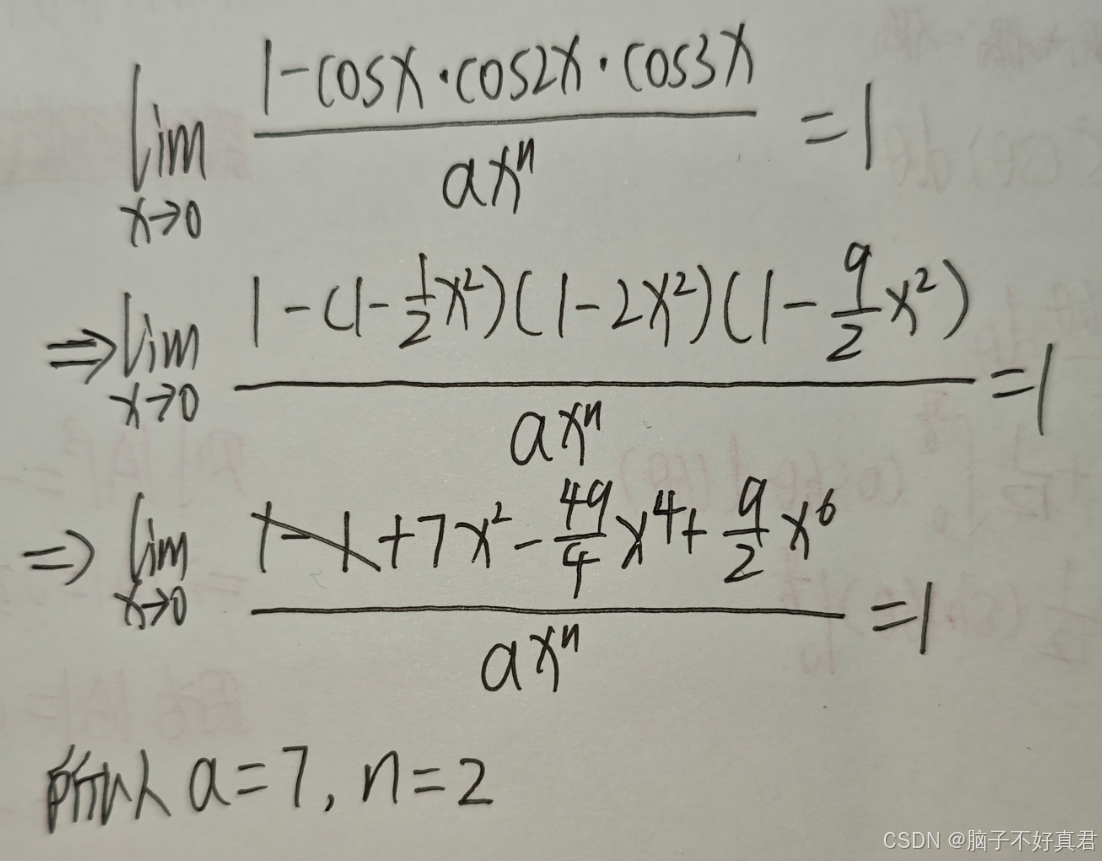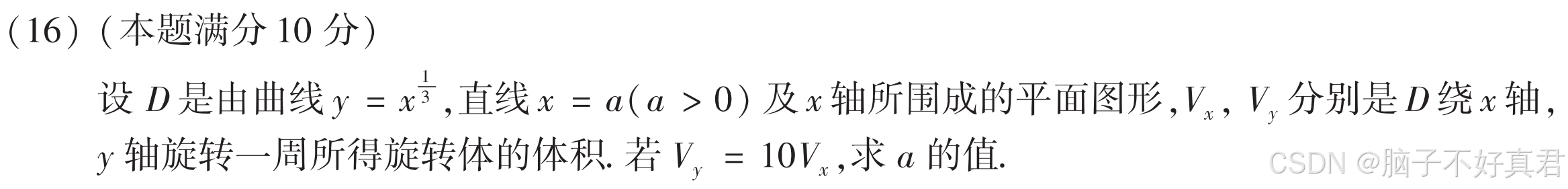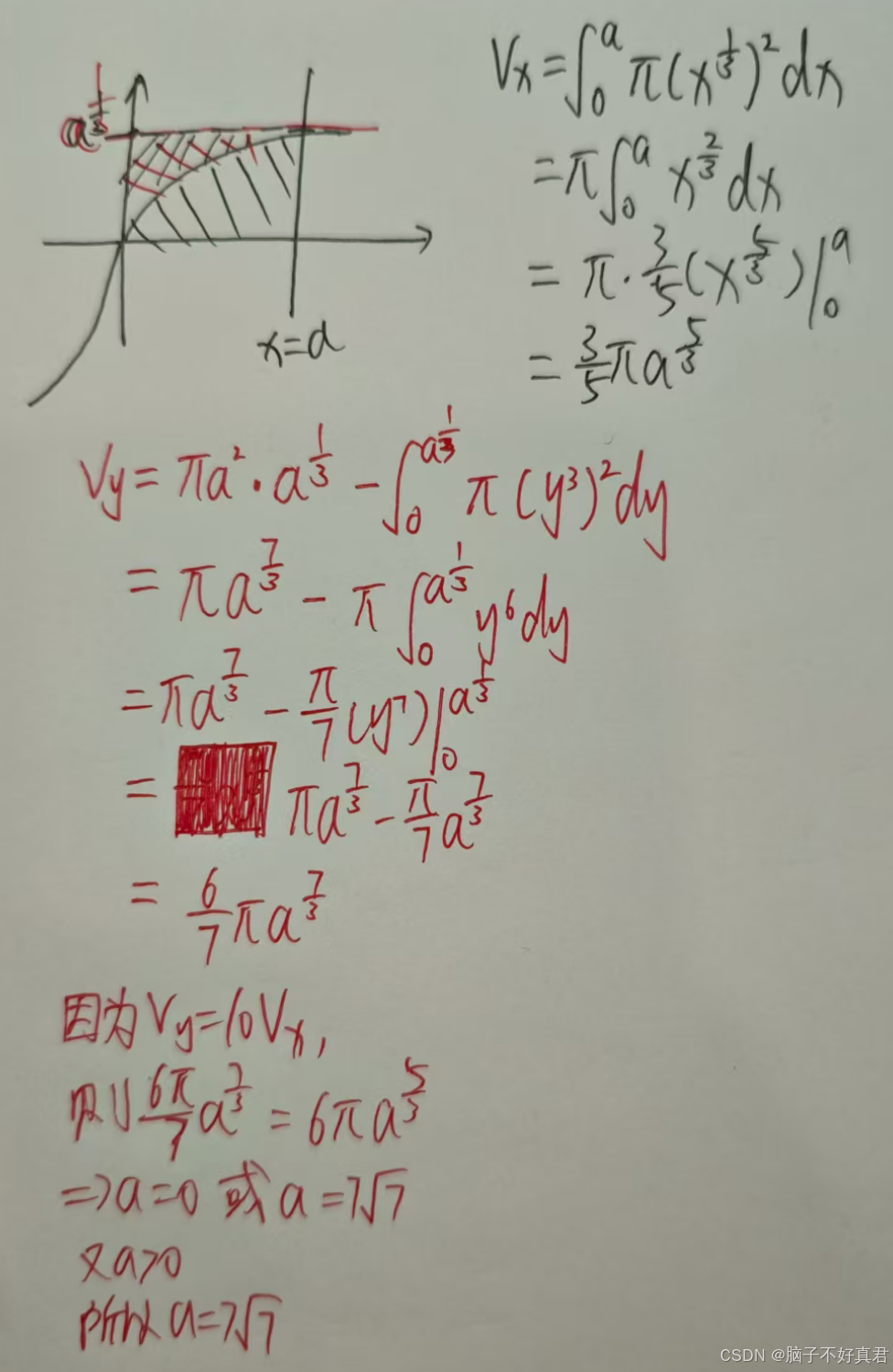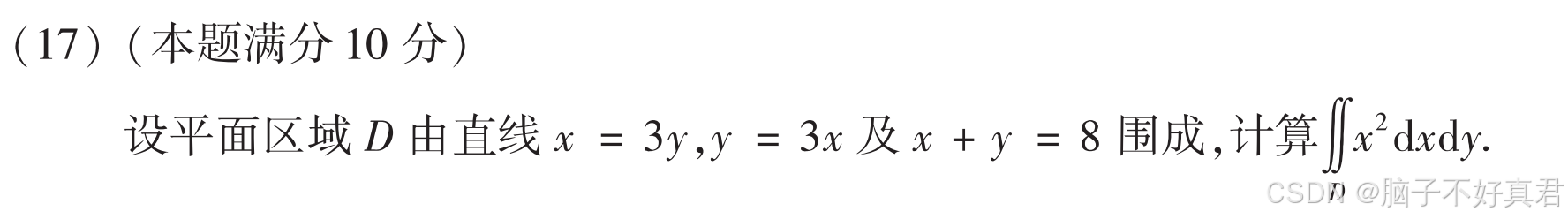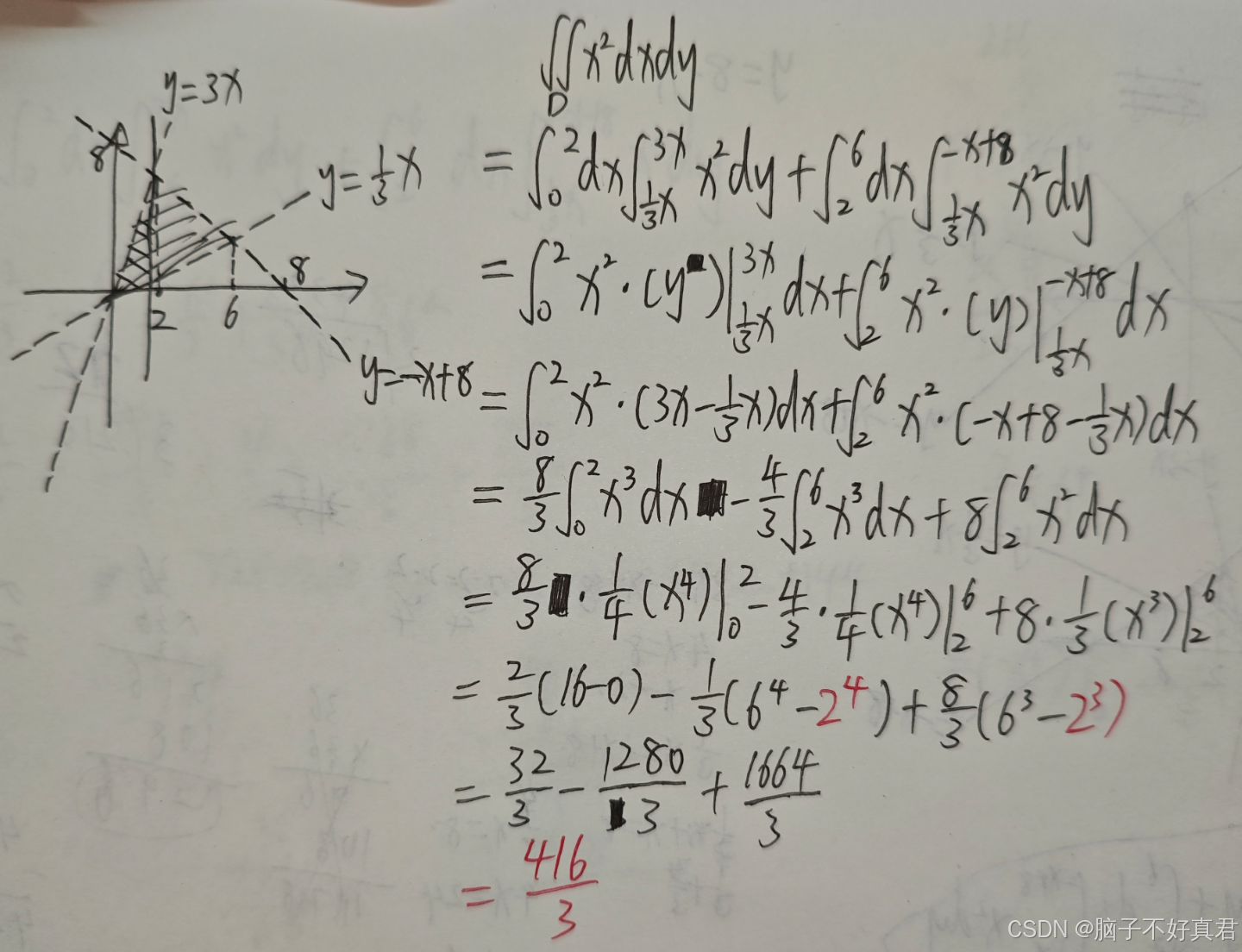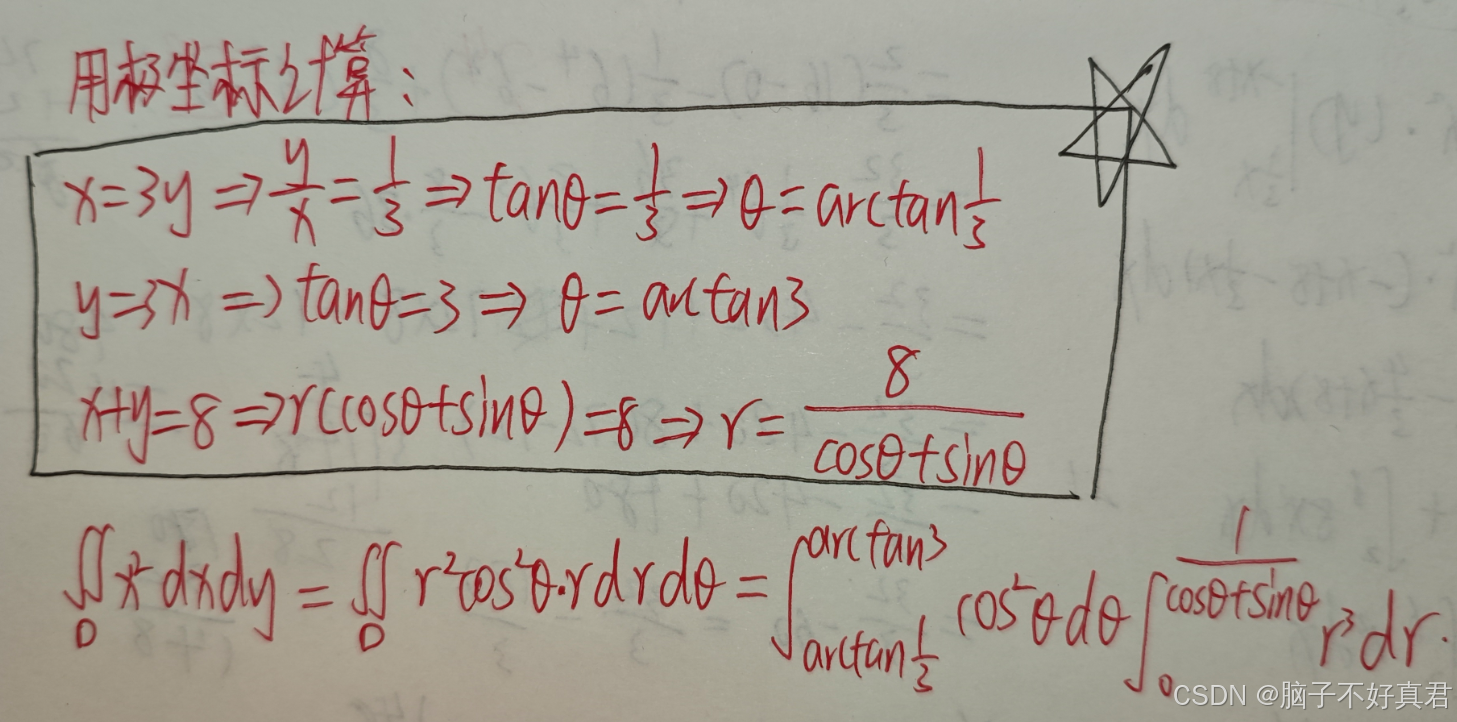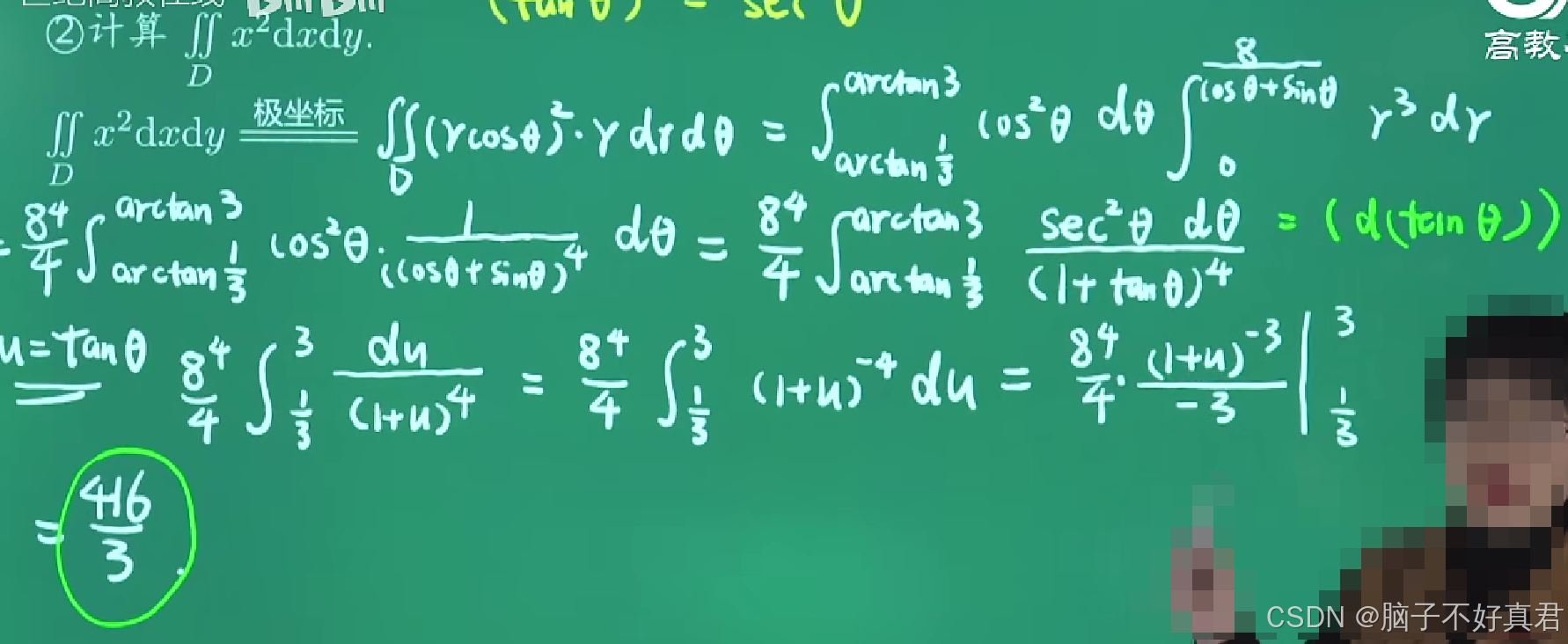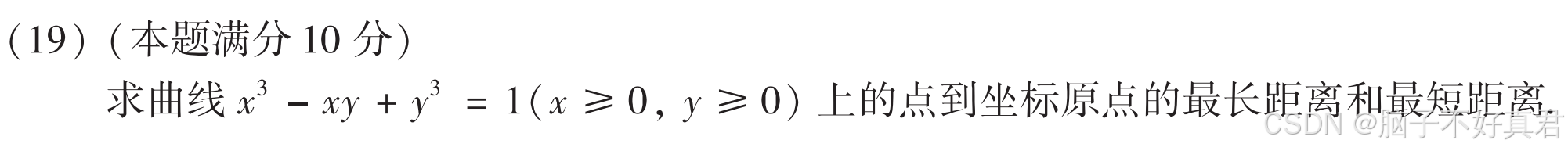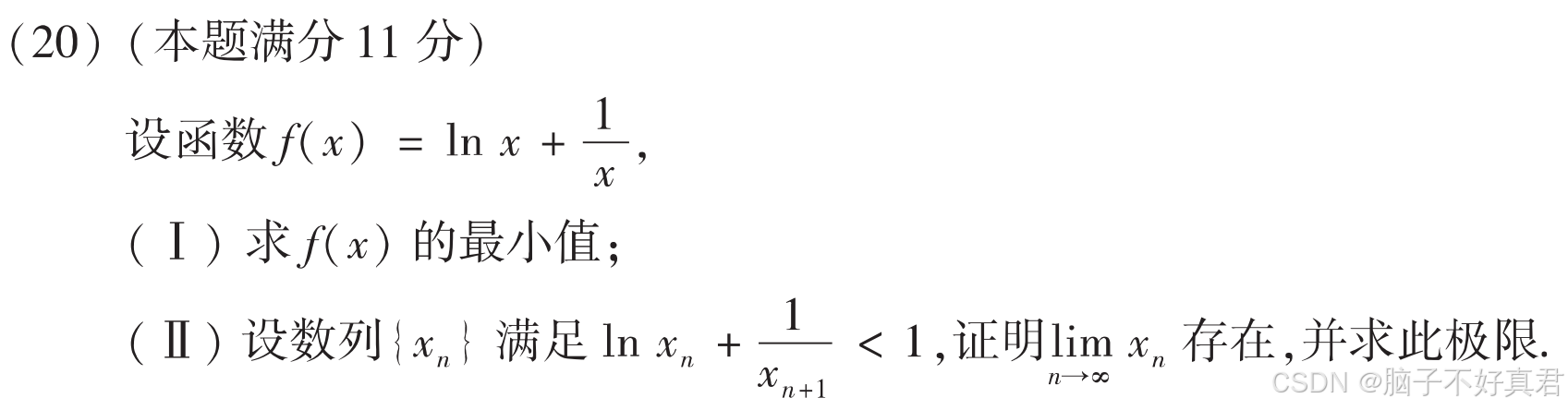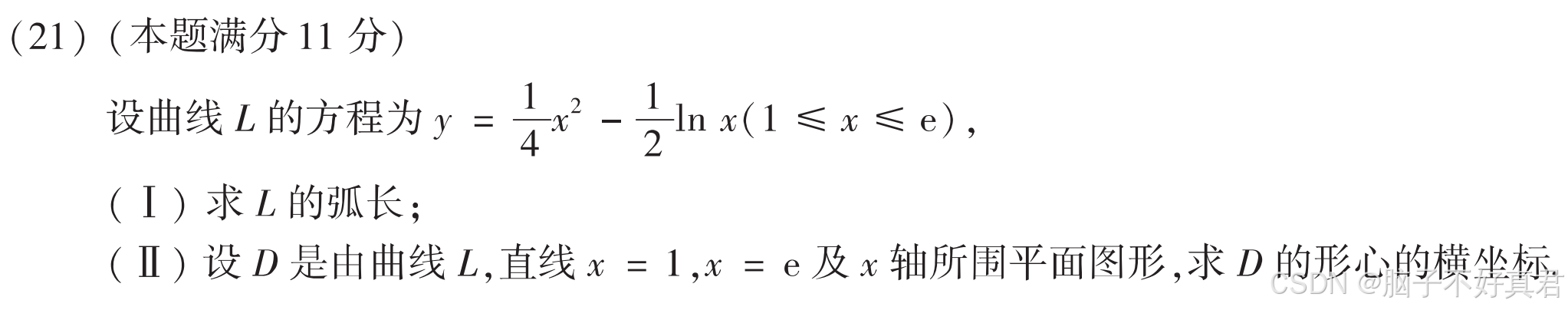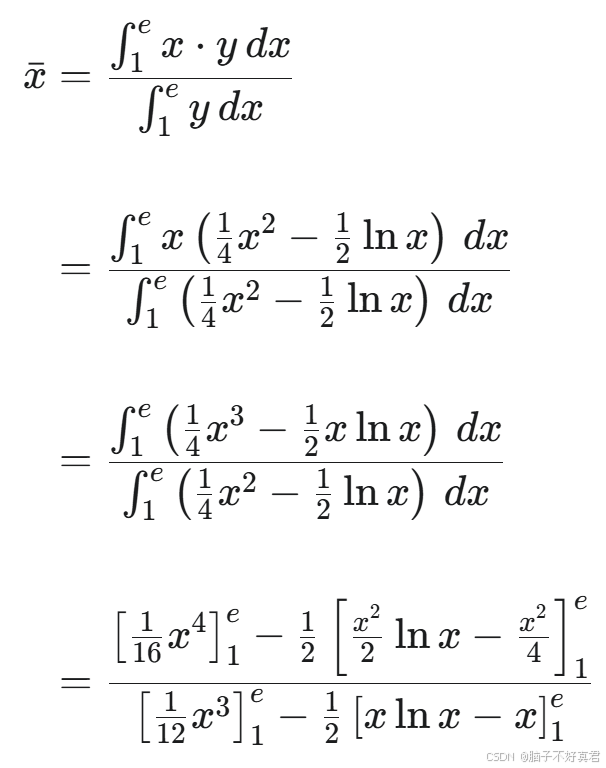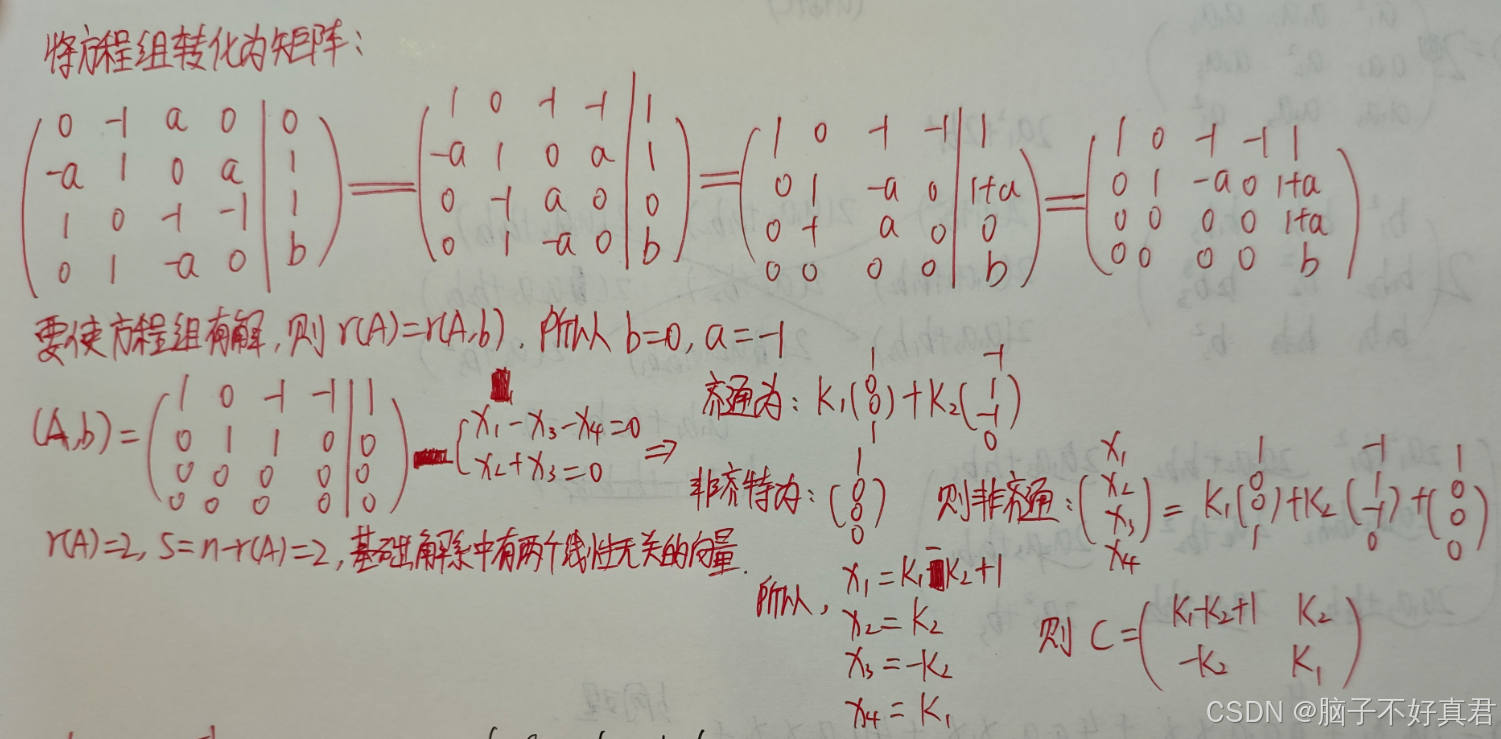一、选择题
(1)
考点:低阶无穷小定义、高阶无穷小定义、同阶无穷小定义、等阶无穷小定义、移项变形/极限存在并且分母→0时则分子也→0
方法一:
方法二:
(2)
考点:说不清楚的思路/凑导数定义式、洛必达法则、隐函数求导
方法一:我的方法
方法二:凑导数定义式
(3)
考点:★第一步最重要的是求出分段函数的分段表达式、洛必达法则、连续定义、导数定义
或利用结论:
(4)
考点:p积分、q积分、无穷积分计算
(5)
考点:复合函数求导法则
(6)
考点:二重积分的结果正负只取决于被积函数的正负、普通对称性、轮换对称性
(7)
考点:矩阵等价⇔矩阵的秩相等、一个矩阵乘以一个可逆矩阵其秩不变、右乘操作列
(8)
**考点:**矩阵可相似对角化的充要条件是有 n 个线性无关的特征向量(即对应特征值的几何重数等于相应的代数重数)/ 实对称矩阵相似的充分必要条件(两实对称矩阵相似⇔特征多项式相同⇔特征值全部相同)
方法一:两实对称矩阵相似⇔特征值全部相同
方法二:矩阵可相似对角化的充要条件
方法三:两实对称矩阵相似⇔特征多项式相同
二、填空题
(9)
考点:a^b=e^blna、ln(1+x)的麦克劳林展开
(10)
考点:反函数求导法则、⬇思路、积分结果为0的两种情况(上限=下限、被积函数恒等于0)
(11)
考点:计算极坐标系下的平面图形面积的积分公、(不是计算极坐标弧长积分)
(12)
考点:法线的定义、参数方程求导
(13)
考点:非齐次特解的差是齐次的解、若有两个解是齐次的解且线性无关则C1解1+C2解2就是齐次的通解(P332)、解1/解2=函数≠常数则两个解线性无关
★新题型(14)
考点:|A|=|A^T|、|AA*|=|A|^n、伴随矩阵定义、拉普拉斯展开
同类型题目
三、解答题
(15)
考点:cosx的麦克劳林展开、等价无穷小的定义
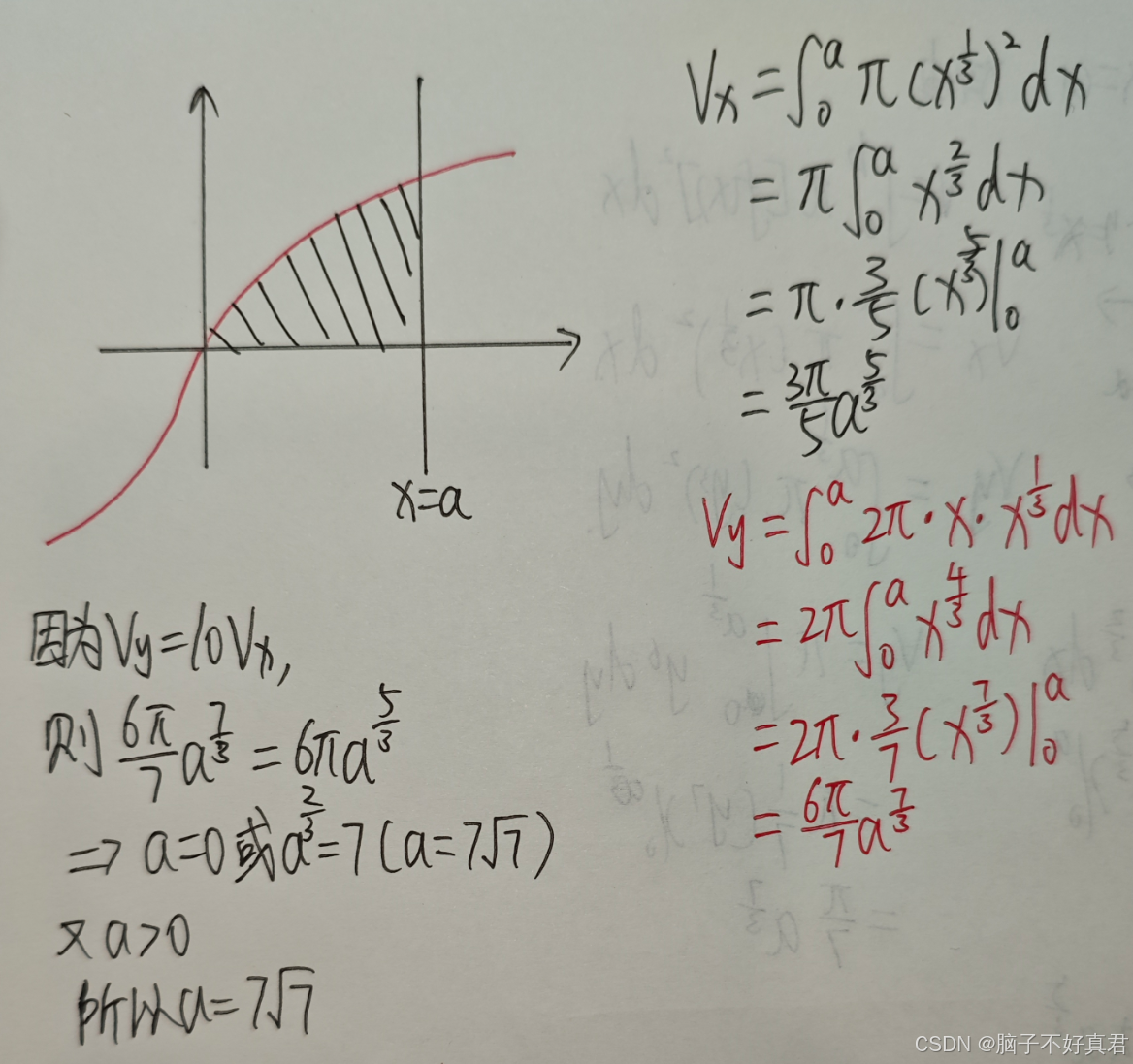
(16)
考点:圆盘法、柱壳法
方法一:一个圆盘法+一个柱壳法
方法二:两个 圆盘法
(17)
考点:计算量
方法一:直角坐标
方法二:极坐标
(18)
考点:奇函数f(x), f(0)=0、奇函数求导是偶函数、偶函数f(x)=f(-x)、注意运动第一问得到的结论、拉格朗日中值定理、罗尔定理、设辅助函数
(Ⅰ)
方法一:拉格朗日中值定理
方法二:辅助函数+罗尔定理
(Ⅱ)
方法一:辅助函数_1+罗尔定理
方法二:辅助函数_2+罗尔定理
★(19)
考点:拉格朗日乘数法、坐标系点与点的距离公式
(20)
考点:n→∞的条件是在计算极限的时候才使用、取极限"<"变等号"<="
(Ⅰ)
(Ⅱ)
(21)
考点:直角坐标系弧长积分公式、平面图形面积积分公式、形心积分公式、描点法判断积分区域
(Ⅰ)
(Ⅱ)
(22)
考点:看下列方法
方法一:转化为增广矩阵解线性方程组
方法二(不推荐):硬解方程组、如果方程组有解且未知数个数 > 方程个数, 则方程组有无穷多解
(23)
考点:
二次型对应矩阵的定义(一个二次型对应着一个对称矩阵.若 A 是一个实对称矩阵,且f=x^T A x,则称 A 为二次型 f 对应的对称矩阵)、
二次型正交变换后的对角矩阵系数就是二次型对称矩阵的特征值、
当 α 是一个单位向量时, 模长为1即 ∣∣α∣∣=1, α^T α=1、
对任何非零 n 维列向量 α,β,矩阵 βa^T的秩均为1(在1000上证过)、
若 A 不满秩, 则 0 也是 A 的一个特征值、
矩阵秩的次加性:两个矩阵和的秩,小于或等于它们各自秩的和
(Ⅰ)
方法一:用向量表示二次型
方法二(不推荐):硬展
(Ⅱ)