机器学习——05 决策树

失散132025-08-12 2:09

1 简介

  • 基本概念：决策树是一种树形结构，用于分类和回归任务。它通过一系列的判断条件将数据逐步划分到不同的类别中。每个内部节点代表一个特征的判断，每个分支代表判断的结果，每个叶子节点代表最终的分类结果；

  • 决策树的建立过程：

    • 特征选择：选择对分类结果影响较大的特征。在女孩相亲的例子中，年龄、长相、收入和是否公务员都是特征；
    • 决策树生成：根据选择的特征，按照一定的规则生成决策树。例如下面的例子中，先根据年龄进行判断，如果年龄大于30岁则直接不见；如果年龄小于等于30岁，则进一步根据长相进行判断；
    • 剪枝：决策树容易出现过拟合现象，即模型在训练数据上表现很好，但在新数据上表现较差。剪枝是一种缓解过拟合的方法，通过去掉一些不必要的分支来简化决策树；

  • 生活中的决策树------女孩相亲：

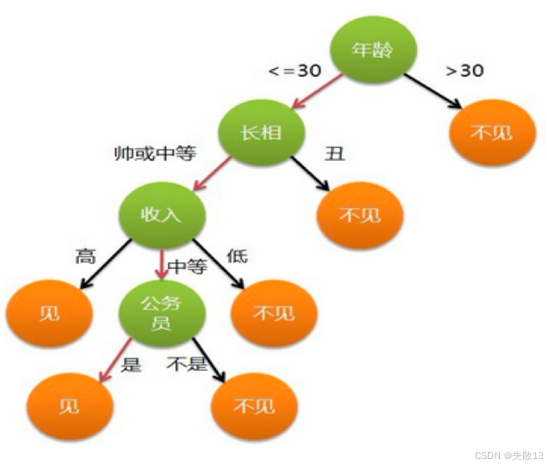
    • 在女孩相亲的决策树中：

      • 年龄是第一个判断条件，如果年龄大于30岁，直接不见

      • 如果年龄小于等于30岁，则判断长相，如果长相丑则不见

      • 如果长相帅或中等，则进一步判断收入

      • 如果收入高则见；如果收入中等，则判断是否公务员，是公务员则见，否则不见；如果收入低则不见

    • 数据预测：

      • 第一行数据（28岁，帅，高收入，非公务员） ：
        • 年龄28岁≤30岁，进入长相判断
        • 长相帅，进入收入判断
        • 收入高，所以预测值为"见"
      • 第二行数据（30岁，丑，高收入，是公务员） ：
        • 年龄30岁≤30岁，进入长相判断
        • 长相丑，所以预测值为"不见"
      • 第三行数据（39岁，帅，中等收入，非公务员） ：
        • 年龄39岁>30岁，所以预测值为"不见"

2 ID3决策树

2.1 信息熵

  • 信息熵（Entropy）是信息论中的一个重要概念，用于衡量随机变量的不确定性程度；

    • 熵越大：意味着数据的不确定性越高，包含的信息量也就越多。例如，一组完全随机的数据，其熵值较大

    • 熵越小：表示数据的不确定性越低，信息量也就越少。例如，一组高度有序的数据，其熵值较小

  • 信息熵的计算公式为：
    H(x)=−∑i=0nP(xi)log⁡2P(xi) H(x) = -\sum_{i=0}^{n} P(x_i) \log_2 P(x_i) H(x)=−i=0∑nP(xi)log2P(xi)

    • 其中：H(x)H(x)H(x) 表示信息熵值、P(xi)P(x_i)P(xi) 表示数据中类别 iii 出现的概率、nnn 表示类别总数；

  • 例1：数据α（ABCDEFGH）和数据β（AAAABCD）

    • 数据α：

      • 包含A、B、C、D、E、F、G、H共8种不同的信息，每种信息出现的概率均为 1/81/81/8；
      • 根据信息熵计算公式可得：

      H(α)=−∑i=0718log⁡218=8×(−18log⁡218)=3 H(\alpha) = -\sum_{i=0}^{7} \frac{1}{8} \log_2 \frac{1}{8} = 8\times(-\frac{1}{8} \log_2 \frac{1}{8}) = 3 H(α)=−i=0∑781log281=8×(−81log281)=3

    • 数据β：

      • 包含A、B、C、D四种信息，其中A出现4次，B出现2次，C和D各出现1次，总共有8个元素；

      • 所以A出现的概率为 4/8=1/24/8 = 1/24/8=1/2，B出现的概率为 2/8=1/42/8 = 1/42/8=1/4，C和D出现的概率均为 1/81/81/8；

      • 根据信息熵计算公式可得：
        H(β)=−12log⁡212−14log⁡214−2×18log⁡218=1.75 H(\beta) = -\frac{1}{2} \log_2 \frac{1}{2} -\frac{1}{4} \log_2 \frac{1}{4} - 2\times\frac{1}{8} \log_2 \frac{1}{8} = 1.75 H(β)=−21log221−41log241−2×81log281=1.75

    • 可以看出，数据α的信息熵大于数据β的信息熵，这是因为数据α的不确定性更高；

  • 例子2：不同类别占比的数据集

    • 例子2-1：

      • 数据集有三个类别，分别占比为 {1/3,1/3,1/3}\{1/3, 1/3, 1/3\}{1/3,1/3,1/3}；
      • 根据信息熵计算公式可得：
        H=−∑i=0213log⁡213=3×(−13log⁡213)≈1.0986 H = -\sum_{i=0}^{2} \frac{1}{3} \log_2 \frac{1}{3} = 3\times(-\frac{1}{3} \log_2 \frac{1}{3}) \approx 1.0986 H=−i=0∑231log231=3×(−31log231)≈1.0986

    • 例子2-2：

      • 数据集有三个类别，分别占比为 {1/10,2/10,7/10}\{1/10, 2/10, 7/10\}{1/10,2/10,7/10}；
      • 根据信息熵计算公式可得：
        H=−110log⁡2110−210log⁡2210−710log⁡2710≈0.8018 H = -\frac{1}{10} \log_2 \frac{1}{10} -\frac{2}{10} \log_2 \frac{2}{10} -\frac{7}{10} \log_2 \frac{7}{10} \approx 0.8018 H=−101log2101−102log2102−107log2107≈0.8018

    • 例子2-3：

      • 数据集有三个类别，分别占比为 {1,0,0}\{1, 0, 0\}{1,0,0}；

      • 根据信息熵计算公式可得：
        H=−1×log⁡21=0 H = -1 \times \log_2 1 = 0 H=−1×log21=0

    • 可以看出，当类别分布越均匀时，信息熵越大；当类别分布越集中时，信息熵越小。当只有一种类别时，信息熵为0，此时数据的不确定性为0。

2.2 信息增益

  • 信息增益是决策树算法中用于选择最优特征的重要指标；

    • 它表示特征A对训练数据集D的信息增益，定义为集合D的熵H(D)与特征A给定条件下D的熵H(D|A)之差；
    • 简单来说，信息增益衡量了使用特征A进行划分后，数据集的不确定性减少的程度；

  • 信息增益的计算公式为：信息增益 = 熵 - 条件熵
    g(D,A)=H(D)−H(D∣A) g(D, A) = H(D) - H(D|A) g(D,A)=H(D)−H(D∣A)

    • 其中：g(D,A)g(D, A)g(D,A) 表示特征A对数据集D的信息增益、H(D)H(D)H(D) 表示数据集D的熵、H(D∣A)H(D|A)H(D∣A) 表示在特征A给定的条件下数据集D的条件熵；

  • 条件熵 H(D∣A)H(D|A)H(D∣A) 的计算公式为：
    H(D∣A)=∑v=1n∣Dv∣∣D∣H(Dv)=∑v=1n∣Dv∣∣D∣∑k=1K∣Dkv∣∣Dv∣log⁡2∣Dkv∣∣Dv∣ H(D|A) = \sum_{v=1}^{n} \frac{|D^v|}{|D|} H(D^v) = \sum_{v=1}^{n} \frac{|D^v|}{|D|} \sum_{k=1}^{K} \frac{|D_k^v|}{|D^v|} \log_2 \frac{|D_k^v|}{|D^v|} H(D∣A)=v=1∑n∣D∣∣Dv∣H(Dv)=v=1∑n∣D∣∣Dv∣k=1∑K∣Dv∣∣Dkv∣log2∣Dv∣∣Dkv∣

    • 其中：DvD^vDv 表示特征A取值为 vvv 的样本子集、∣Dv∣|D^v|∣Dv∣ 表示 DvD^vDv 的样本数量、DkvD_k^vDkv 表示 DvD^vDv 中属于类别 kkk 的样本子集、∣Dkv∣|D_k^v|∣Dkv∣ 表示 DkvD_k^vDkv 的样本数量、KKK 表示类别总数；

  • 例：

    • 已知有6个样本，根据特征A的取值（α和β），对应的目标值如下：

      特征A 目标值
      α A
      α A
      β B
      α A
      β B
      α B

      • α部分对应的目标值为：AAAB（共4个样本）

      • β部分对应的目标值为：BB（共2个样本）

    • 计算条件熵

      • 条件为α的熵 ：α部分有4个样本，其中A出现3次，B出现1次。概率分别为 3/43/43/4 和 1/41/41/4，根据熵的计算公式可得：
        H(α)=−34log⁡234−14log⁡214≈0.81 H(\alpha) = -\frac{3}{4} \log_2 \frac{3}{4} - \frac{1}{4} \log_2 \frac{1}{4} \approx 0.81 H(α)=−43log243−41log241≈0.81

      • 条件为β的熵 ：β部分有2个样本，都为B。概率为 2/2=12/2 = 12/2=1，根据熵的计算公式可得：
        H(β)=−1×log⁡21=0 H(\beta) = -1 \times \log_2 1 = 0 H(β)=−1×log21=0

      • 条件熵 ：α部分占总样本数的 4/64/64/6，β部分占总样本数的 2/62/62/6。根据条件熵的计算公式可得：
        H(D∣A)=46×0.81+26×0=0.54 H(D|A) = \frac{4}{6} \times 0.81 + \frac{2}{6} \times 0 = 0.54 H(D∣A)=64×0.81+62×0=0.54

    • 计算熵 。总共有6个样本，其中A出现3次，B出现3次。概率分别为 3/6=1/23/6 = 1/23/6=1/2 和 3/6=1/23/6 = 1/23/6=1/2，根据熵的计算公式可得：
      H(D)=−36log⁡236−36log⁡236=1 H(D) = -\frac{3}{6} \log_2 \frac{3}{6} - \frac{3}{6} \log_2 \frac{3}{6} = 1 H(D)=−63log263−63log263=1

    • 计算信息增益 。根据信息增益的计算公式可得：
      g(D,A)=H(D)−H(D∣A)=1−0.54=0.46 g(D, A) = H(D) - H(D|A) = 1 - 0.54 = 0.46 g(D,A)=H(D)−H(D∣A)=1−0.54=0.46

2.3 ID3决策树构建流程

  1. 计算每个特征的信息增益 ：信息增益用于衡量特征对数据集分类的贡献程度，计算公式为 g(D,A)=H(D)−H(D∣A)g(D, A) = H(D) - H(D|A)g(D,A)=H(D)−H(D∣A)，其中 H(D)H(D)H(D) 是数据集 DDD 的熵，H(D∣A)H(D|A)H(D∣A) 是在特征 AAA 给定条件下数据集 DDD 的条件熵；
  2. 使用信息增益最大的特征将数据集拆分为子集：选择信息增益最大的特征，根据该特征的不同取值将数据集划分为多个子集。
  3. 使用该特征作为决策树的一个节点：将信息增益最大的特征作为当前决策树的一个节点。
  4. 使用剩余特征对子集重复上述过程：对每个子集，重复步骤1-3，直到所有特征都被使用或满足停止条件。

2.4 案例

  • 以某论坛客户流失率数据为例，考察性别和活跃度特征对流失率的影响，看看哪一个特征对流失率的影响更大；

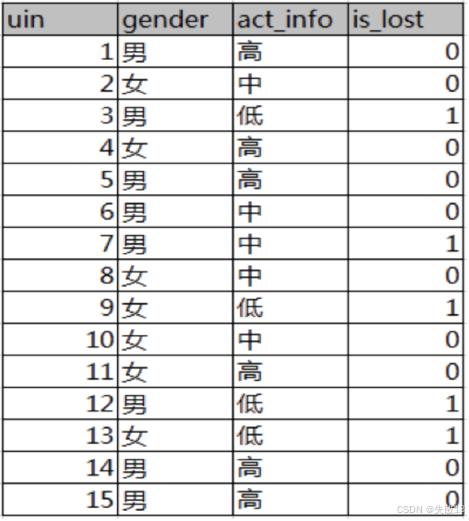
  • 步骤：

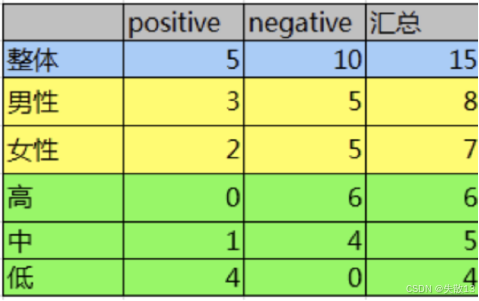
    1. 计算熵 H(D)H(D)H(D) ：已知数据集有15条样本，其中5个正样本（流失）和10个负样本（未流失）
      H(D)=−515log⁡2515−1015log⁡21015≈0.9812 H(D) = -\frac{5}{15} \log_2 \frac{5}{15} - \frac{10}{15} \log_2 \frac{10}{15} \approx 0.9812 H(D)=−155log2155−1510log21510≈0.9812

    2. 计算性别条件熵 H(D∣性别)H(D|性别)H(D∣性别) ：性别分为男性和女性，男性有8个样本（3个正样本，5个负样本），女性有7个样本（2个正样本，5个负样本）
      H(D∣性别)=815×(−38log⁡238−58log⁡258)+715×(−27log⁡227−57log⁡257) H(D|性别) = \frac{8}{15} \times (-\frac{3}{8} \log_2 \frac{3}{8} - \frac{5}{8} \log_2 \frac{5}{8}) + \frac{7}{15} \times (-\frac{2}{7} \log_2 \frac{2}{7} - \frac{5}{7} \log_2 \frac{5}{7}) H(D∣性别)=158×(−83log283−85log285)+157×(−72log272−75log275)

    3. 计算性别信息增益 g(D,性别)g(D, 性别)g(D,性别) ：
      g(D,性别)=H(D)−H(D∣性别)≈0.0064 g(D, 性别) = H(D) - H(D|性别) \approx 0.0064 g(D,性别)=H(D)−H(D∣性别)≈0.0064

    4. 计算活跃度条件熵 H(D∣活跃度)H(D|活跃度)H(D∣活跃度) ：活跃度分为高、中、低，高活跃度有6个样本（0个正样本，6个负样本），中活跃度有5个样本（1个正样本，4个负样本），低活跃度有4个样本（4个正样本，0个负样本）
      H(D∣活跃度)=615×0+515×(−15log⁡215−45log⁡245)+415×0 H(D|活跃度) = \frac{6}{15} \times 0 + \frac{5}{15} \times (-\frac{1}{5} \log_2 \frac{1}{5} - \frac{4}{5} \log_2 \frac{4}{5}) + \frac{4}{15} \times 0 H(D∣活跃度)=156×0+155×(−51log251−54log254)+154×0

    5. 计算活跃度信息增益 g(D,活跃度)g(D, 活跃度)g(D,活跃度) ：
      g(D,活跃度)=H(D)−H(D∣活跃度)≈0.6776 g(D, 活跃度) = H(D) - H(D|活跃度) \approx 0.6776 g(D,活跃度)=H(D)−H(D∣活跃度)≈0.6776

  • 结论：活跃度的信息增益（约0.6776）比性别的信息增益（约0.0064）大，说明活跃度对用户流失的影响比性别大；

    • 高中低指的是活跃度的高中低；

3 C4.5决策树

3.1 ID3树的不足

  • ID3树偏向于选择种类多的特征作为分裂依据；

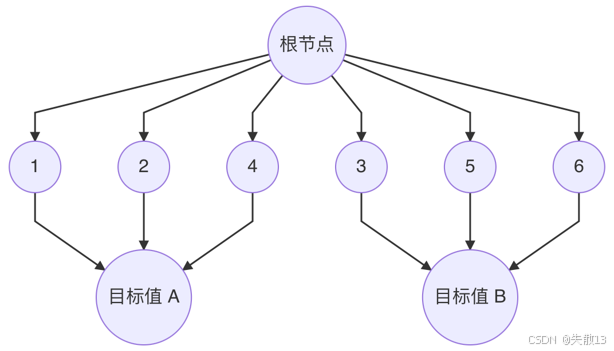
  • 例如：

    特征b 特征a 目标值
    1 α A
    2 α A
    3 β B
    4 α A
    5 β B
    6 α B

    • 特征b有6个取值，而特征a只有2个取值；

    • 在决策树构建中，如果选择特征 b 作为分裂特征，每次分裂可以根据特征 b 的不同取值将数据集划分到不同的子节点中，可能会构造一棵深度为2的决策树；

      决策树的深度是指从根节点到叶子节点的最长路径的边数

      深度为 2 意味着这棵决策树最多有两层分裂

      例如，根节点是第一层分裂，根据特征 b 的取值将数据集划分为多个子集，每个子集再进行一次分裂（第二层分裂），然后得到叶子节点（即分类结果）

    • 由于特征 b 的取值较多，能够将数据集划分得比较细致，使得每个叶子节点中的样本尽可能属于同一类别。因此，在训练集上，这棵决策树能够很好地拟合数据，预测准确率可能会很高；

    • 但是决策树过于依赖特征 b 进行分裂，而忽略了其他可能有用的特征。当遇到新的数据时，由于模型只学习了特征 b 与目标值之间的关系，而没有考虑其他特征的影响，可能无法准确地进行预测，从而导致过拟合；

3.2 信息增益率

  • 信息增益率是决策树算法中用于选择最优特征的指标，它是信息增益与特征熵的比值。信息增益率的计算公式为：
    Gain_Ratio(D,a)=Gain(D,a)IV(a) \text{Gain\_Ratio}(D, a) = \frac{\text{Gain}(D, a)}{\text{IV}(a)} Gain_Ratio(D,a)=IV(a)Gain(D,a)

    • 其中：

      • Gain(D,a)\text{Gain}(D, a)Gain(D,a) 表示特征 aaa 对数据集 DDD 的信息增益。

      • IV(a)\text{IV}(a)IV(a) 表示特征 aaa 的特征熵，计算公式为：
        IV(a)=−∑v=1n∣Dv∣∣D∣log⁡2∣Dv∣∣D∣ \text{IV}(a) = -\sum_{v=1}^{n} \frac{|D^v|}{|D|} \log_2 \frac{|D^v|}{|D|} IV(a)=−v=1∑n∣D∣∣Dv∣log2∣D∣∣Dv∣

      • DvD^vDv 是特征 aaa 取值为 vvv 的样本子集，∣Dv∣|D^v|∣Dv∣ 是 DvD^vDv 的样本数量，∣D∣|D|∣D∣ 是数据集 DDD 的样本总数；

  • 信息增益率的本质：

    • 信息增益率是对信息增益的修正，它增加了一个惩罚系数；
    • 当特征取值个数较多时，惩罚系数较小；当特征取值个数较少时，惩罚系数较大；
    • 惩罚系数实际上是数据集 DDD 以特征 aaa 作为随机变量的熵的倒数。

3.3 案例

  • 给定数据集，计算特征 aaa 和特征 bbb 的信息增益率

    特征b 特征a 目标值
    1 α A
    2 α A
    3 β B
    4 α A
    5 β B
    6 α B

    1. 特征 aaa 的信息增益率

      • 信息增益（Gain(D,a)Gain(D, a)Gain(D,a)）

        • 首先计算数据集 DDD 的熵 H(D)H(D)H(D)：
          H(D)=−∑k=1K∣Ck∣∣D∣log⁡2∣Ck∣∣D∣=−36log⁡236−36log⁡236=1 H(D) = -\sum_{k=1}^{K} \frac{|C_k|}{|D|} \log_2 \frac{|C_k|}{|D|}= -\frac{3}{6} \log_2 \frac{3}{6} - \frac{3}{6} \log_2 \frac{3}{6}=1 H(D)=−k=1∑K∣D∣∣Ck∣log2∣D∣∣Ck∣=−63log263−63log263=1

          • 其中，CkC_kCk 是数据集 DDD 中属于类别 kkk 的样本子集，∣Ck∣|C_k|∣Ck∣ 是 CkC_kCk 的样本数量，∣D∣|D|∣D∣ 是数据集 DDD 的样本总数，KKK 是类别总数

          从给定的数据集中可以看到，总共有 6 条样本数据，所以 D=6D=6D=6

          属于类别 AAA 的样本有 3 条（第 1、2、4 条数据），所以 C1C_1C1 =3（这里 k=1k=1k=1 对应类别 AAA）

          属于类别 BBB 的样本有 3 条（第 3、5、6 条数据），所以 C2C_2C2 = 3（这里 k=2k=2k=2 对应类别 BBB）

        • 然后计算在特征 aaa 给定条件下数据集 DDD 的条件熵 H(D∣a)H(D|a)H(D∣a)：
          H(D∣a)=∑v=1V∣Dv∣∣D∣H(Dv)=46×(−34log⁡234−14log⁡214)+26×0=0.54 H(D|a) = \sum_{v=1}^{V} \frac{|D^v|}{|D|} H(D^v) = \frac{4}{6} \times (-\frac{3}{4} \log_2 \frac{3}{4} - \frac{1}{4} \log_2 \frac{1}{4}) + \frac{2}{6} \times 0=0.54 H(D∣a)=v=1∑V∣D∣∣Dv∣H(Dv)=64×(−43log243−41log241)+62×0=0.54

          • 其中，DvD^vDv 是特征 aaa 取值为 vvv 的样本子集，∣Dv∣|D^v|∣Dv∣ 是 DvD^vDv 的样本数量，VVV 是特征 aaa 的取值个数，H(Dv)H(D^v)H(Dv) 是子集 DvD^vDv 的熵

          1.确定特征 aaa 的取值个数 VVV 以及每个取值 vvv 对应的样本子集 DvD^vDv 的样本数量 ∣Dv∣|D^v|∣Dv∣。特征 aaa 有两种取值，分别是 α\alphaα 和 β\betaβ，所以 V=2V = 2V=2

          • 当特征 aaa 取值为 α\alphaα 时（v=1v = 1v=1），对应的样本子集 D1D^1D1 包含第1、2、4、6条数据，共4条样本，所以 ∣D1∣=4|D^1| = 4∣D1∣=4
          • 当特征 aaa 取值为 β\betaβ 时（v=2v = 2v=2），对应的样本子集 D2D^2D2 包含第3、5条数据，共2条样本，所以 ∣D2∣=2|D^2| = 2∣D2∣=2

          2.计算 ∣Dv∣∣D∣\frac{|D^v|}{|D|}∣D∣∣Dv∣

          • 对于 v=1v = 1v=1（特征 aaa 取值为 α\alphaα），∣D1∣∣D∣=46\frac{|D^1|}{|D|} = \frac{4}{6}∣D∣∣D1∣=64
          • 对于 v=2v = 2v=2（特征 aaa 取值为 β\betaβ），∣D2∣∣D∣=26\frac{|D^2|}{|D|} = \frac{2}{6}∣D∣∣D2∣=62

          3.计算子集 DvD^vDv 的熵 H(Dv)H(D^v)H(Dv)

          • 对于 v=1v = 1v=1（特征 aaa 取值为 α\alphaα） ：子集 D1D^1D1 中的样本目标值有 AAA 和 BBB。其中，目标值为 AAA 的样本有3条（第1、2、4条数据），目标值为 BBB 的样本有1条（第6条数据）。根据熵的计算公式：
            H(D1)=−34log⁡234−14log⁡214 H(D^1) = -\frac{3}{4} \log_2 \frac{3}{4} - \frac{1}{4} \log_2 \frac{1}{4} H(D1)=−43log243−41log241
          • 对于 v=2v = 2v=2（特征 aaa 取值为 β\betaβ） ：子集 D2D^2D2 中的样本目标值都为 BBB，所以熵为0，即 H(D2)=0H(D^2) = 0H(D2)=0。

          4.计算条件熵 H(D∣a)H(D|a)H(D∣a)。将上述计算结果代入条件熵的计算公式：
          H(D∣a)=46×(−34log⁡234−14log⁡214)+26×0=0.54 H(D|a) = \frac{4}{6} \times (-\frac{3}{4} \log_2 \frac{3}{4} - \frac{1}{4} \log_2 \frac{1}{4}) + \frac{2}{6} \times 0 = 0.54 H(D∣a)=64×(−43log243−41log241)+62×0=0.54

        • 最后计算信息增益：
          Gain(D,a)=H(D)−H(D∣a)=1−0.54=0.46 Gain(D, a) = H(D) - H(D|a) = 1 - 0.54 = 0.46 Gain(D,a)=H(D)−H(D∣a)=1−0.54=0.46

      • 特征熵（IV(a)IV(a)IV(a)）
        IV(a)=−∑v=1V∣Dv∣∣D∣log⁡2∣Dv∣∣D∣=−46log⁡246−26log⁡226=0.92 IV(a) = -\sum_{v=1}^{V} \frac{|D^v|}{|D|} \log_2 \frac{|D^v|}{|D|}= -\frac{4}{6} \log_2 \frac{4}{6} - \frac{2}{6} \log_2 \frac{2}{6} = 0.92 IV(a)=−v=1∑V∣D∣∣Dv∣log2∣D∣∣Dv∣=−64log264−62log262=0.92

      • 信息增益率（Gain_Ratio(D,a)Gain\_Ratio(D, a)Gain_Ratio(D,a)）
        Gain_Ratio(D,a)=Gain(D,a)IV(a)=Gain(D,a)IV(a)=0.460.92=0.5 Gain\_Ratio(D, a) = \frac{Gain(D, a)}{IV(a)}= \frac{Gain(D, a)}{IV(a)} = \frac{0.46}{0.92} = 0.5 Gain_Ratio(D,a)=IV(a)Gain(D,a)=IV(a)Gain(D,a)=0.920.46=0.5

    2. 特征 bbb 的信息增益率

      • 信息增益：

        • 首先计算数据集 DDD 的熵 H(D)H(D)H(D)，公式同上：
          H(D)=−36log⁡236−36log⁡236 H(D) = -\frac{3}{6} \log_2 \frac{3}{6} - \frac{3}{6} \log_2 \frac{3}{6} H(D)=−63log263−63log263

        • 然后计算在特征 bbb 给定条件下数据集 DDD 的条件熵 H(D∣b)H(D|b)H(D∣b)：
          H(D∣b)=6×0 H(D|b) = 6 \times 0 H(D∣b)=6×0

        • 最后计算信息增益：
          Gain(D,b)=H(D)−H(D∣b)=1−0=1 Gain(D, b) = H(D) - H(D|b) = 1 - 0 = 1 Gain(D,b)=H(D)−H(D∣b)=1−0=1

      • 特征熵 ：
        IV(b)=−16log⁡216×6=2.58 IV(b) = -\frac{1}{6} \log_2 \frac{1}{6} \times 6 = 2.58 IV(b)=−61log261×6=2.58

      • 信息增益率 ：
        Gain_Ratio(D,b)=Gain(D,b)IV(b)=12.58≈0.39 Gain\_Ratio(D, b) = \frac{Gain(D, b)}{IV(b)} = \frac{1}{2.58} \approx 0.39 Gain_Ratio(D,b)=IV(b)Gain(D,b)=2.581≈0.39

    • 结论：特征 aaa 的信息增益率（0.50.50.5）大于特征 bbb 的信息增益率（0.390.390.39），根据信息增益率，应该选择特征 aaa 作为分裂特征。

4 CART分类树

4.1 概述

  • CART（Classification and Regression Tree）决策树是一种功能强大的决策树模型，它既可以用于分类任务，也可以用于回归任务

    • CART回归树 ：使用平方误差最小化策略来选择最优特征和分裂点
    • CART分类树 ：采用基尼指数最小化策略来选择最优特征和分裂点

  • 下面先介绍CART分类树。

4.2 基尼值和基尼指数

  • 基尼值（Gini(D)） ：表示从数据集 DDD 中随机抽取两个样本，其类别标记不一致的概率。基尼值越小，数据集 DDD 的纯度越高。计算公式为：
    Gini(D)=∑k=1∣y∣∑k′≠kpkpk′=1−∑k=1∣y∣pk2 \text{Gini}(D) = \sum_{k=1}^{|y|} \sum_{k' \neq k} p_k p_{k'} = 1 - \sum_{k=1}^{|y|} p_k^2 Gini(D)=k=1∑∣y∣k′=k∑pkpk′=1−k=1∑∣y∣pk2

    • 其中，pkp_kpk 是数据集 DDD 中属于类别 kkk 的样本比例，∣y∣|y|∣y∣ 是类别总数；

  • 基尼指数（Gini_index(D)） ：用于选择使划分后基尼系数最小的属性作为最优化分属性。计算公式为：
    Gini_index(D,a)=∑v=1V∣Dv∣∣D∣Gini(Dv) \text{Gini\index}(D, a) = \sum{v=1}^{V} \frac{|D^v|}{|D|} \text{Gini}(D^v) Gini_index(D,a)=v=1∑V∣D∣∣Dv∣Gini(Dv)

    • 其中，DvD^vDv 是特征 aaa 取值为 vvv 的样本子集，∣Dv∣|D^v|∣Dv∣ 是 DvD^vDv 的样本数量，VVV 是特征 aaa 的取值个数；

  • 注意：

    • 信息增益（ID3）、信息增益率值越大（C4.5），则说明优先选择该特征；
    • 基尼指数值越小（CART），则说明优先选择该特征。

4.3 案例

  • 以是否拖欠贷款数据为例，计算各特征的基尼指数，选择最优分裂点；

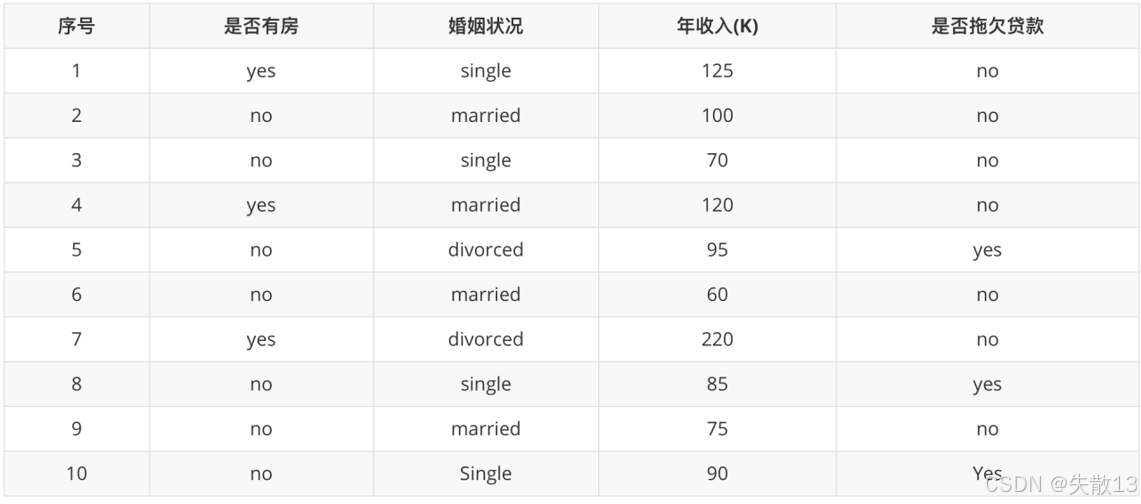
  • 是否有房

    • 有房子的基尼值 ：有房子的样本有3个（第1、4、7条数据），目标值都为 nonono。根据基尼值的计算公式：
      Gini(是否有房, yes)=1−(03)2−(33)2=0 \text{Gini(是否有房, yes)} = 1 - \left(\frac{0}{3}\right)^2 - \left(\frac{3}{3}\right)^2 = 0 Gini(是否有房, yes)=1−(30)2−(33)2=0

      对于有房子的样本，目标值只有 nonono，所以 pno=33=1p_{no} = \frac{3}{3} = 1pno=33=1，pyes=03=0p_{yes} = \frac{0}{3} = 0pyes=30=0

      代入公式可得：Gini(是否有房, yes)=1−(03)2−(33)2=0\text{Gini(是否有房, yes)} = 1 - \left(\frac{0}{3}\right)^2 - \left(\frac{3}{3}\right)^2 = 0Gini(是否有房, yes)=1−(30)2−(33)2=0

    • 无房子的基尼值 ：无房子的样本有7个（第2、3、5、6、8、9、10条数据），其中目标值为 nonono 的有4个，目标值为 yesyesyes 的有3个。根据基尼值的计算公式：
      Gini(是否有房, no)=1−(37)2−(47)2≈0.4898 \text{Gini(是否有房, no)} = 1 - \left(\frac{3}{7}\right)^2 - \left(\frac{4}{7}\right)^2 \approx 0.4898 Gini(是否有房, no)=1−(73)2−(74)2≈0.4898

    • 基尼指数 ：有房子的样本占总样本数的 3/103/103/10，无房子的样本占总样本数的 7/107/107/10。根据基尼指数的计算公式：
      Gini_index(D,是否有房)=710×0.4898+310×0=0.343 \text{Gini\_index}(D, 是否有房) = \frac{7}{10} \times 0.4898 + \frac{3}{10} \times 0 = 0.343 Gini_index(D,是否有房)=107×0.4898+103×0=0.343

  • 婚姻状况

    • 计算 {married} 和 {single, divorced} 情况下的基尼指数
      • 结婚的基尼值 ：结婚的样本有4个（第2、4、6、9条数据），目标值都为 nonono。根据基尼值的计算公式：
        Gini_index(D,married)=0 \text{Gini\_index}(D, married) = 0 Gini_index(D,married)=0
      • 不结婚的基尼值 ：不结婚的样本有6个（第1、3、5、7、8、10条数据），其中目标值为 nonono 的有3个，目标值为 yesyesyes 的有3个。根据基尼值的计算公式：
        Gini_index(D,single,divorced)=1−(36)2−(36)2=0.5 \text{Gini\_index}(D, single, divorced) = 1 - \left(\frac{3}{6}\right)^2 - \left(\frac{3}{6}\right)^2 = 0.5 Gini_index(D,single,divorced)=1−(63)2−(63)2=0.5
      • 以 married 作为分裂点的基尼指数 ：
        Gini_index(D,married)=410×0+610×0.5=0.3 \text{Gini\_index}(D, married) = \frac{4}{10} \times 0 + \frac{6}{10} \times 0.5 = 0.3 Gini_index(D,married)=104×0+106×0.5=0.3
    • 计算 {single} | {married, divorced} 情况下的基尼指数 ：
      Gini_index(D,婚姻状况)=410×0.5+610×[1−(16)2−(56)2]=0.367 \text{Gini\_index}(D, 婚姻状况) = \frac{4}{10} \times 0.5 + \frac{6}{10} \times \left[1 - \left(\frac{1}{6}\right)^2 - \left(\frac{5}{6}\right)^2\right] = 0.367 Gini_index(D,婚姻状况)=104×0.5+106×[1−(61)2−(65)2]=0.367
    • 计算 {divorced} | {single, married} 情况下的基尼指数 ：
      Gini_index(D,婚姻状况)=210×0.5+810×[1−(28)2−(68)2]=0.4 \text{Gini\_index}(D, 婚姻状况) = \frac{2}{10} \times 0.5 + \frac{8}{10} \times \left[1 - \left(\frac{2}{8}\right)^2 - \left(\frac{6}{8}\right)^2\right] = 0.4 Gini_index(D,婚姻状况)=102×0.5+108×[1−(82)2−(86)2]=0.4
    • 结论 ：该特征的基尼值为 0.30.30.3，预选分裂点为 {married} 和 {single, divorced}；

  • 年收入

    • 确定待确定的分裂点 ：将年收入数值型属性升序排列，以相邻中间值作为待确定分裂点，得到分裂点为 656565、72.572.572.5、808080、87.787.787.7、92.592.592.5、97.597.597.5、110110110、122.5122.5122.5、172.5172.5172.5；

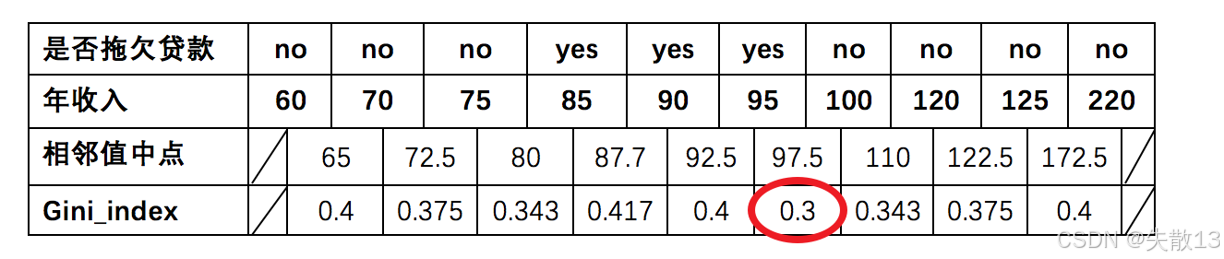
    • 计算各分裂点的基尼指数：

      • 以年收入 656565 将样本分为两部分，计算基尼指数：
        Gini_index(D,年收入=65)=110×0+910×[1−(69)2−(39)2]=0.4 \text{Gini\_index}(D, 年收入=65) = \frac{1}{10} \times 0 + \frac{9}{10} \times \left[1 - \left(\frac{6}{9}\right)^2 - \left(\frac{3}{9}\right)^2\right] = 0.4 Gini_index(D,年收入=65)=101×0+109×[1−(96)2−(93)2]=0.4
      • 以此类推计算所有分割点的基尼指数，最小的基尼指数为 0.30.30.3（对应分裂点 97.597.597.5）

  • 决策树构建过程

    • 第1轮结果

      • 以是否有房作为分裂点的基尼指数为 0.3430.3430.343

      • 以婚姻状况为分裂特征、以 married 作为分裂点的基尼指数为 0.30.30.3

      • 以年收入作为分裂特征、以 97.597.597.5 作为分裂点的基尼指数为 0.30.30.3

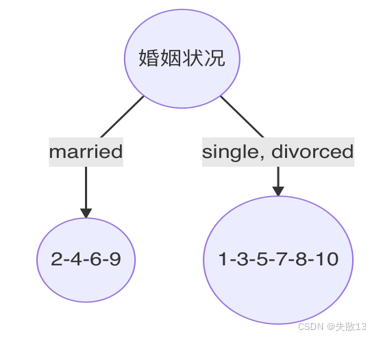
    • 第2轮

      • 样本 222、444、666、999 的类别都是 nonono，已经达到最大纯度，该节点不需要再继续分裂

      • 样本 111、333、555、777、888、101010 中仍然包含 444 个 nonono 和 222 个 yesyesyes，该节点未达到要求的纯度，需要继续划分

      • 右子树的数据集变为 111、333、555、777、888、101010，在该数据集中计算不同特征的基尼指数，选择基尼指数最小的特征继续分裂

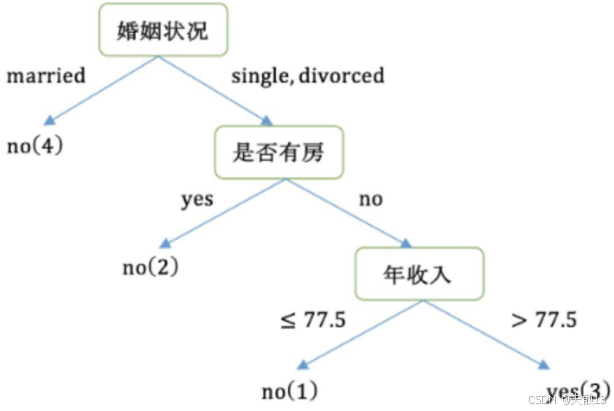
    • 重复上述过程，直到构建完成整个决策树。

4.4 三种决策树的对比

名称 提出时间 分支方式 特点
ID3 1975 信息增益 1. ID3只能对离散属性的数据集构成决策树 2. 倾向于选择取值较多的属性
C4.5 1993 信息增益率 1. 缓解了ID3分支过程中总喜欢偏向选择值较多的属性 2. 可处理连续数值型属性，也增加了对缺失值的处理方法 3. 只适合于能够驻留于内存的数据集，大数据集无能为力
CART 1984 基尼指数 1. 可以进行分类和回归，可处理离散属性，也可以处理连续属性 2. 采用基尼指数，计算量减小 3. 一定是二叉树

5 案例：泰坦尼克号生存预测

5.1 决策树API介绍

  • 类定义 ：class sklearn.tree.DecisionTreeClassifier(criterion='gini', max_depth=None, random_state=None)
  • 参数说明 ：
    • criterion ：特征选择标准，可选"gini"（代表基尼系数，默认，对应 CART 算法）或"entropy"（代表信息增益）
    • min_samples_split：内部节点再划分所需的最小样本数
    • min_samples_leaf：叶子节点最少样本数
    • max_depth：决策树的最大深度

5.2 案例：泰坦尼克号生存预测

  • 案例背景：

    • 1912年4月15日，在她的处女航中，泰坦尼克号在与冰山相撞后沉没，在2224名乘客和机组人员中造成1502人死亡；
    • 造成海难失事的原因之一是乘客和机组人员没有足够的救生艇。尽管是否能够幸存有一些运气因素，但有些人比其他人更容易生存，比如妇女，儿童和上流社会；
    • 有了遇难和幸运数据，运用机器学习工具来预测哪些乘客可幸免于悲剧；

  • 数据情况：

    • 数据集中的特征包括：

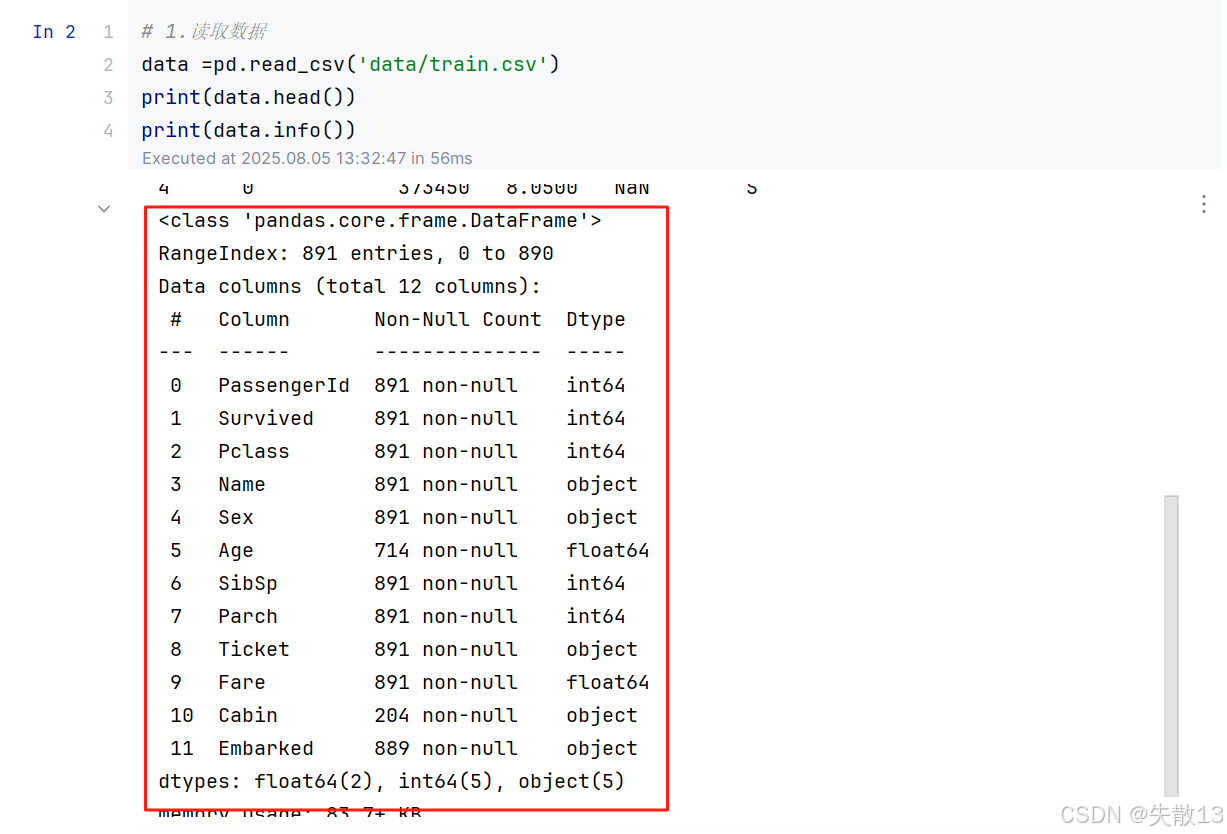
    • Pclass是社会经济阶层的代码；

    • age存在数据缺失；

  • 导包：

    python 复制代码 
    # 0.导包
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import classification_report
from sklearn.tree import plot_tree
import matplotlib.pyplot as plt

  • 读取数据：

    python 复制代码 
    # 1.读取数据
data =pd.read_csv('data/train.csv')
print(data.head())
print(data.info())

  • 数据处理：

    python 复制代码 
    # 2.数据处理
x = data[['Pclass', 'Sex', 'Age']].copy()
y = data['Survived'].copy()
print(x.head(10))
# 对x中的'Age'列的缺失值进行处理，使用'Age'列的均值来填充缺失值，并且直接在原数据上进行修改（inplace=True）
x['Age'].fillna(x['Age'].mean(), inplace=True)
print(x.head(10))
# 对x进行独热编码处理，将分类变量转换为虚拟变量
x = pd.get_dummies(x)
# 打印处理后x的前10行数据，查看独热编码后的数据形式
print(x.head(10))
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)

    独热编码（One-Hot Encoding）是一种将分类变量转换为数值型变量的编码方式。它通过创建一个二进制向量来表示每个分类变量的不同取值。

    原理 ：对于一个具有 nnn 个不同取值的分类变量，独热编码会将其转换为 nnn 个二进制列。每个二进制列对应一个取值，当该取值出现时，对应的二进制列为 111，其余为 000。

    示例：假设有一个分类变量"颜色"，其取值为"红"、"绿"、"蓝"。使用独热编码后，会生成三个新的二进制列："颜色_红"、"颜色_绿"、"颜色_蓝"。对于每个样本：

    • 如果样本的颜色是"红"，则"颜色_红"为 111，"颜色_绿"和"颜色_蓝"为 000
    • 如果样本的颜色是"绿"，则"颜色_绿"为 111，"颜色_红"和"颜色_蓝"为 000
    • 如果样本的颜色是"蓝"，则"颜色_蓝"为 111，"颜色_红"和"颜色_绿"为 000

    作用：独热编码的主要作用是将分类变量转换为数值型变量，以便于机器学习算法处理。许多机器学习算法（如决策树、逻辑回归等）只能处理数值型数据，而不能直接处理分类数据。通过独热编码，可以将分类数据转换为数值型数据，从而使得这些算法能够处理分类数据。

    优点：

    1. 能够有效地处理分类变量。
    2. 不会引入新的顺序关系，因为每个分类变量的取值都是独立的。

    缺点：

    1. 当分类变量的取值较多时，会生成大量的新列，可能导致维度灾难。
    2. 会增加数据的稀疏性。

    在泰坦尼克号乘客生存预测案例中，使用pd.get_dummies(x)对x进行独热编码处理，就是将x中的分类变量（如Pclass、Sex）转换为数值型变量，以便于后续的机器学习算法处理。

  • 模型训练：

    python 复制代码 
    # 3.模型训练
model =DecisionTreeClassifier()
model.fit(x_train,y_train)

  • 模型评估：

    python 复制代码 
    # 4.模型评估
y_pre = model.predict(x_test)
# 打印分类报告，该报告包含了模型在测试集上的精确率、召回率、F1分数等评估指标
print(classification_report(y_true=y_test,y_pred=y_pre))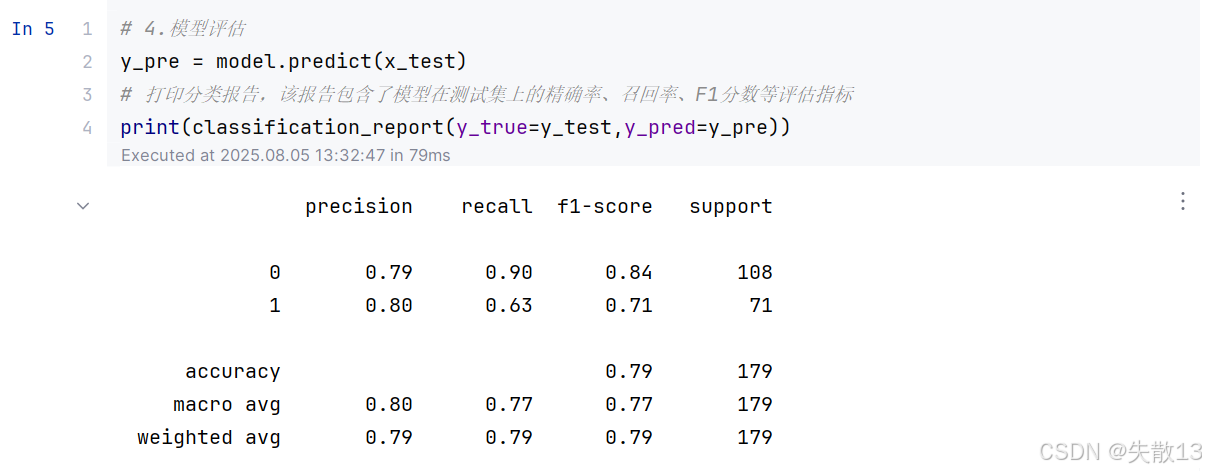

    precision（精确率）：模型预测为正类的样本中，实际为正类的比例

    • 类别 0 的精确率为 0.79，表示模型预测为类别 0 的样本中，有 79% 的样本实际为类别 0
    • 类别 1 的精确率为 0.80，表示模型预测为类别 1 的样本中，有 80% 的样本实际为类别 1

    recall（召回率）：实际为正类的样本中，被模型预测为正类的比例

    • 类别 0 的召回率为 0.90，表示实际为类别 0 的样本中，有 90% 的样本被模型预测为类别 0
    • 类别 1 的召回率为 0.63，表示实际为类别 1 的样本中，有 63% 的样本被模型预测为类别 1

    f1-score（F1 分数）：精确率和召回率的调和平均值，综合考虑了精确率和召回率

    • 类别 0 的 F1 分数为 0.84
    • 类别 1 的 F1 分数为 0.71

    support（支持数）：每个类别的样本数量

    • 类别 0 有 108 个样本
    • 类别 1 有 71 个样本

    accuracy（准确率）：模型预测正确的样本数占总样本数的比例，为 0.79

    macro avg（宏平均）：对每个类别的评估指标进行平均

    • 宏平均精确率为 0.80
    • 宏平均召回率为 0.77
    • 宏平均 F1 分数为 0.77

    weighted avg（加权平均）：根据每个类别的样本数量对评估指标进行加权平均

    • 加权平均精确率为 0.79
    • 加权平均召回率为 0.79
    • 加权平均 F1 分数为 0.79

  • 可视化：

    python 复制代码 
    # 5.可视化
plot_tree(model)
plt.show()

6 CART回归树

6.1 CART回归树 VS CART分类树

  1. 预测输出：

    • CART分类树预测输出的是一个离散值
    • CART回归树预测输出的是一个连续值

    **离散值（Discrete Values）**是指只能取特定的、不连续的值的数据。这些值通常是整数，且相邻两个值之间没有其他可能的取值

    • 特点：取值是有限的或可数的；相邻两个值之间没有中间值。
    • 示例 ：
      • 性别：男、女。
      • 年龄分组：儿童、青年、中年、老年。
      • 产品评分：1星、2星、3星、4星、5星。
    • 应用场景 ：
      • 分类问题：例如，判断一封邮件是垃圾邮件还是正常邮件。
      • 计数问题：例如，统计一个班级的学生人数。

    **连续值（Continuous Values）**是指可以在一定范围内取任意值的数据。这些值可以是整数，也可以是小数，且相邻两个值之间可以有无限多个中间值。

    • 特点：取值是无限的或不可数的；相邻两个值之间可以有中间值。
    • 示例 ：
      • 身高：1.75米、1.76米、1.77米等。
      • 体重：65.5公斤、65.6公斤、65.7公斤等。
      • 温度：25.5℃、25.6℃、25.7℃等。
    • 应用场景 ：
      • 回归问题：例如，预测房价、股票价格等。
      • 测量问题：例如，测量物体的长度、重量、温度等。

    区别总结

    特征 离散值 连续值
    取值方式 只能取特定的、不连续的值 可以在一定范围内取任意值
    取值数量 有限的或可数的 无限的或不可数的
    相邻值之间是否有中间值 没有 有
    示例 性别、年龄分组、产品评分 身高、体重、温度
    应用场景 分类问题、计数问题 回归问题、测量问题

    在实际应用中，离散值和连续值的处理方法有所不同。例如，在构建决策树时，对于离散值，通常采用信息增益或基尼指数等方法来选择最优划分点；对于连续值，则需要将其离散化，然后再进行处理。

  2. 划分依据：

    • CART分类树使用基尼指数作为划分、构建树的依据
    • CART回归树使用平方损失作为划分、构建树的依据

  3. 叶子节点预测：

    • 分类树使用叶子节点多数类别作为预测类别
    • 回归树则采用叶子节点里均值作为预测输出

6.2 简介

  • CART回归树的平方损失公式为：

    Loss(y,f(x))=(f(x)−y)2 \text{Loss}(y, f(x)) = (f(x) - y)^2 Loss(y,f(x))=(f(x)−y)2

    • 其中，f(x)f(x)f(x) 是模型对样本 xxx 的预测值，yyy 是样本 xxx 的真实值；

  • 以一个只有1个特征 xxx 和目标值 yyy 的数据集为例，构建CART回归树

    • 排序特征并确定待划分点：

      • 将特征 xxx 的值排序，并取相邻元素均值作为待划分点；

      • 例如，特征 xxx 的值为 1,2,3,4,5,6,7,8,9,101, 2, 3, 4, 5, 6, 7, 8, 9, 101,2,3,4,5,6,7,8,9,10，对应的待划分点为 1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.51.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5, 8.5, 9.51.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5；

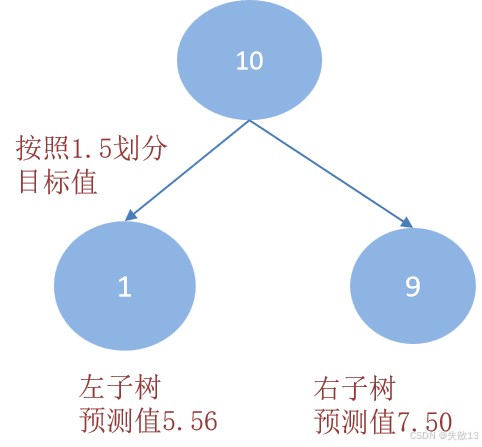
    • 计算每个划分点的平方损失 。以划分点 1.51.51.5 为例：

      • R1R1R1 为小于 1.51.51.5 的样本个数，样本数量为 111，其输出值为 5.565.565.56，即 R1=5.56R1 = 5.56R1=5.56

      • R2R2R2 为大于 1.51.51.5 的样本个数，样本数量为 999，其输出值为：
        R2=5.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.059=7.50 R2 = \frac{5.7 + 5.91 + 6.4 + 6.8 + 7.05 + 8.9 + 8.7 + 9 + 9.05}{9} = 7.50 R2=95.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.05=7.50

      • 该划分点的平方损失为：
        L(1.5)=(5.56−5.56)2+[(5.7−7.5)2+(5.91−7.5)2+⋯+(9.05−7.5)2]=0+15.72=15.72 L(1.5) = (5.56 - 5.56)^2 + [(5.7 - 7.5)^2 + (5.91 - 7.5)^2 + \dots + (9.05 - 7.5)^2] = 0 + 15.72 = 15.72 L(1.5)=(5.56−5.56)2+[(5.7−7.5)2+(5.91−7.5)2+⋯+(9.05−7.5)2]=0+15.72=15.72

    • 确定最优划分点：

      • 计算所有待划分点的平方损失，选择平方损失最小的划分点作为最优划分点；

      • 例如，当划分点 s=6.5s = 6.5s=6.5 时，平方损失 m(s)m(s)m(s) 最小，所以第1个划分变量为特征 xxx，切分点为 6.56.56.5；

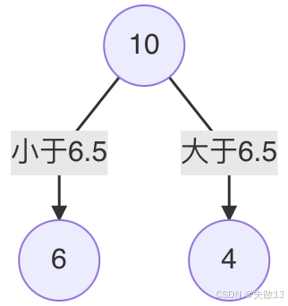
    • 递归划分：

      • 对左子树的6个节点计算每个划分点的平方损失，找出最优划分点；

      • 例如，当 s=3.5s = 3.5s=3.5 时，平方损失 m(s)m(s)m(s) 最小，所以左子树继续以 3.53.53.5 进行分裂；

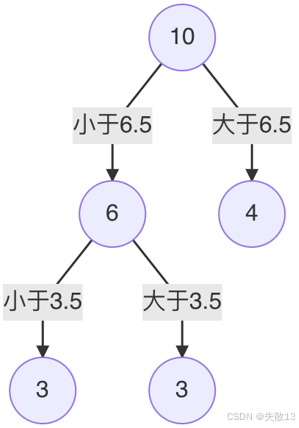
    • 停止划分：假设在生成3个区域之后停止划分，最终得到回归树。每个叶子节点的输出为挂在该节点上的所有样本均值。

  • CART回归树构建过程小结

    • 选择一个特征，将该特征的值进行排序，取相邻点计算均值 作为待划分点
    • 根据所有划分点，将数据集分成两部分：R1R1R1 和 R2R2R2
    • R1R1R1 和 R2R2R2 两部分的平方损失相加作为该切分点平方损失
    • 取最小的平方损失的划分点，作为当前特征的划分点
    • 以此计算其他特征的最优划分点、以及该划分点对应的损失值
    • 在所有的特征的划分点中，选择出最小平方损失的划分点，作为当前树的分裂点

6.3 CART回归树 VS 线性回归

  • 已知数据：

    x 1 2 3 4 5 6 7 8 9 10
    y 5.56 5.7 5.91 6.4 6.8 7.05 8.9 8.7 9 9.05

  • 需求：分别训练线性回归模型和回归决策树模型，并对它们的预测效果进行对比；

  • 导包：

    python 复制代码 
    # 0 导包
import numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt

  • 数据：

    python 复制代码 
    # 1.数据
x = np.array(list(range(1,11))).reshape(-1,1)
y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05])

    reshape(-1, 1) 的作用：

    • 第二个参数 1 表示调整后数组的列数固定为 1
    • 第一个参数 -1 是一个特殊值，表示 "自动计算该维度的大小"，即根据原始数组的总元素数和其他维度的固定值，自动推断出合适的行数

  • 模型训练：

    python 复制代码 
    # 2.模型训练
model1 = DecisionTreeRegressor(max_depth=1)
model2 = DecisionTreeRegressor(max_depth=3)
model3 = LinearRegression()

model1.fit(x,y)
model2.fit(x,y)
model3.fit(x,y)

  • 模型预测：

    python 复制代码 
    # 3.模型预测
x_test = np.arange(0.0, 10.0, 0.01).reshape(-1, 1)
y_pre1 = model1.predict(x_test)
y_pre2 = model2.predict(x_test)
y_pre3 = model3.predict(x_test)

  • 可视化：

    python 复制代码 
    # 4.可视化
plt.figure(figsize=(10, 6), dpi=100)
# 绘制原始数据的散点图，标签为'data'
plt.scatter(x, y, label='data')
plt.plot(x_test, y_pre1,label='max_depth=1')  # 深度为1层
plt.plot(x_test, y_pre2, label='max_depth=3') # 深度为3层
plt.plot(x_test, y_pre3, label='linear')
plt.xlabel('data')
plt.ylabel('target')
plt.title('DecisionTreeRegressor')
# 左上角
plt.legend()
plt.show()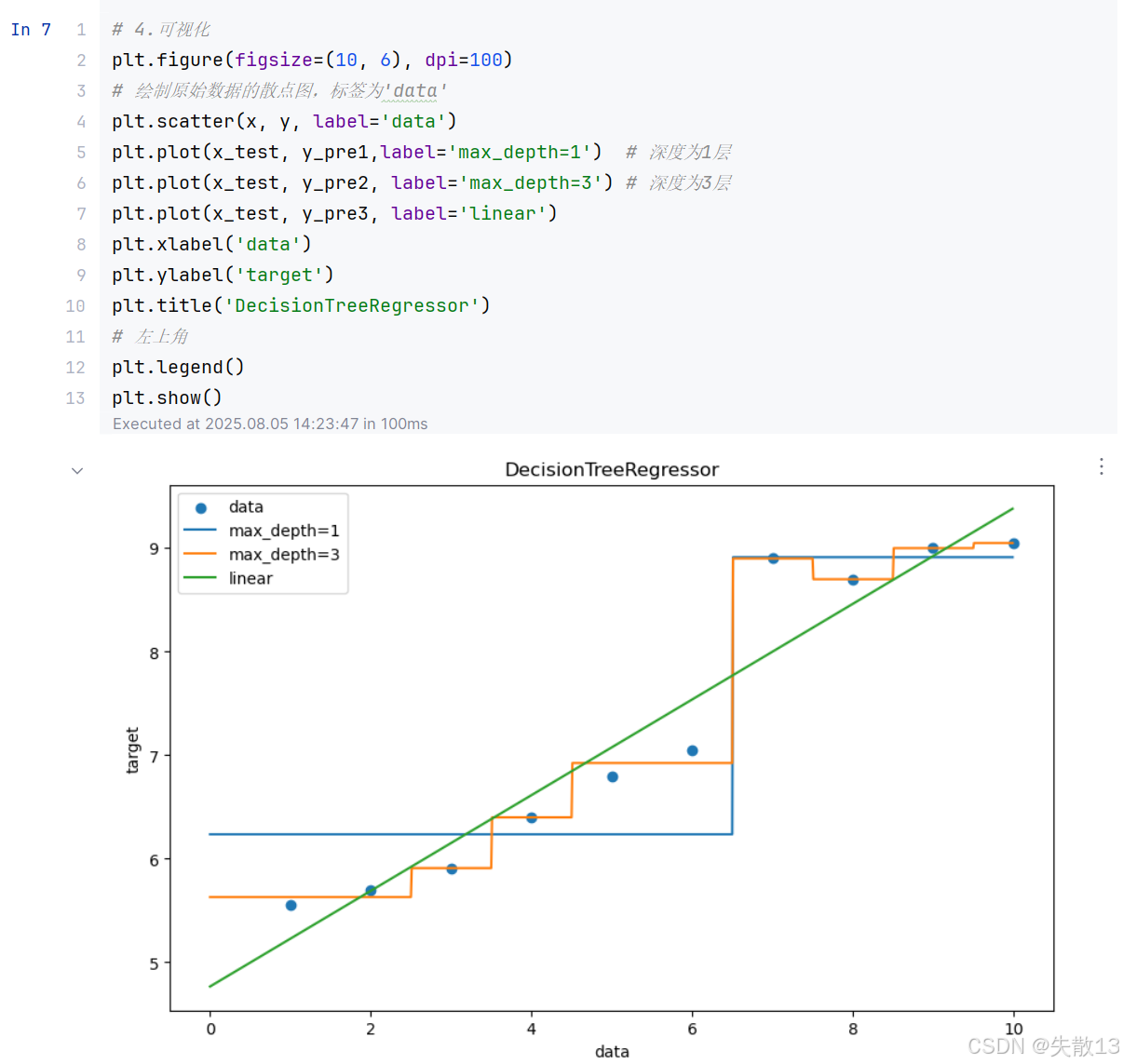

  • 结论：

    • 线性回归是一条直线，决策树是曲线
    • 树的拟合能力是很强的，易过拟合

7 剪枝

7.1 决策树正则化 - 剪枝

  1. **为什么要剪枝？**决策树剪枝是一种防止决策树过拟合的正则化方法，通过剪枝可以提高决策树的泛化能力；
  2. 剪枝：剪枝是指将子树的节点全部删掉，使用叶子节点来替换；
  3. 剪枝方法
    • 预剪枝：在决策树生成过程中，对每个节点在划分前先进行估计。若当前节点的划分不能带来决策树泛化性能的提升，则停止划分并将当前节点标记为叶节点；
    • 后剪枝：先从训练集生成一棵完整的决策树，然后自底向上地对非叶节点进行考察。若将该节点对应的子树替换为叶节点能带来决策树泛化性能的提升，则将该子树替换为叶节点。

7.2 预剪枝&后剪枝

  • 已知：数据集和验证集

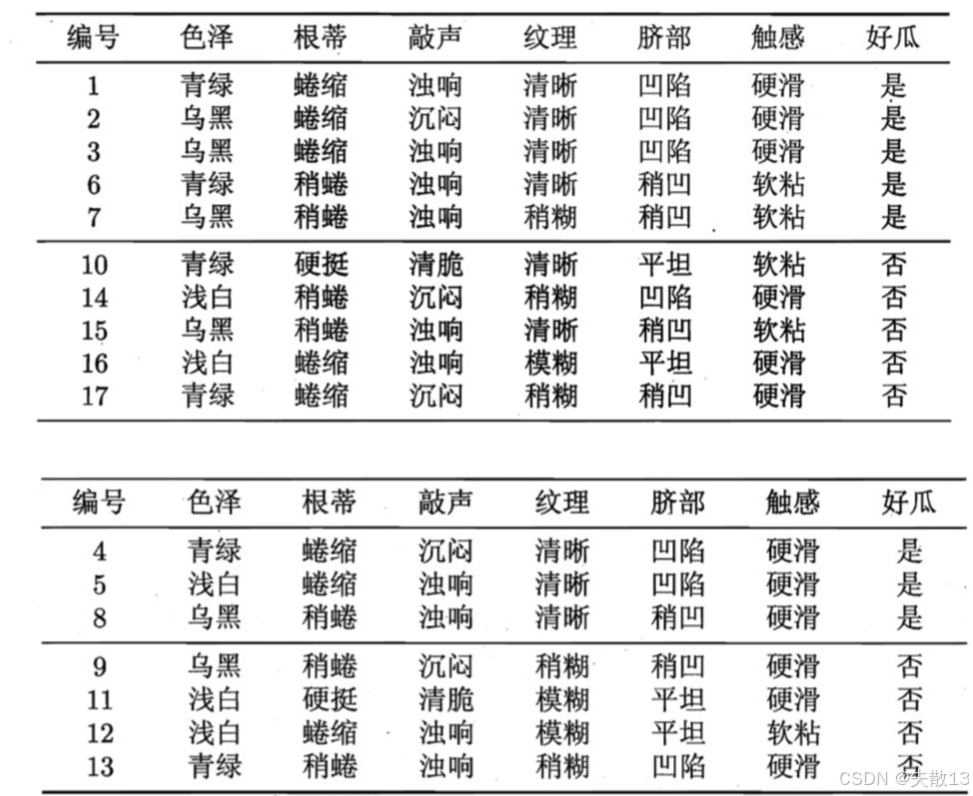
  • 决策树如下：

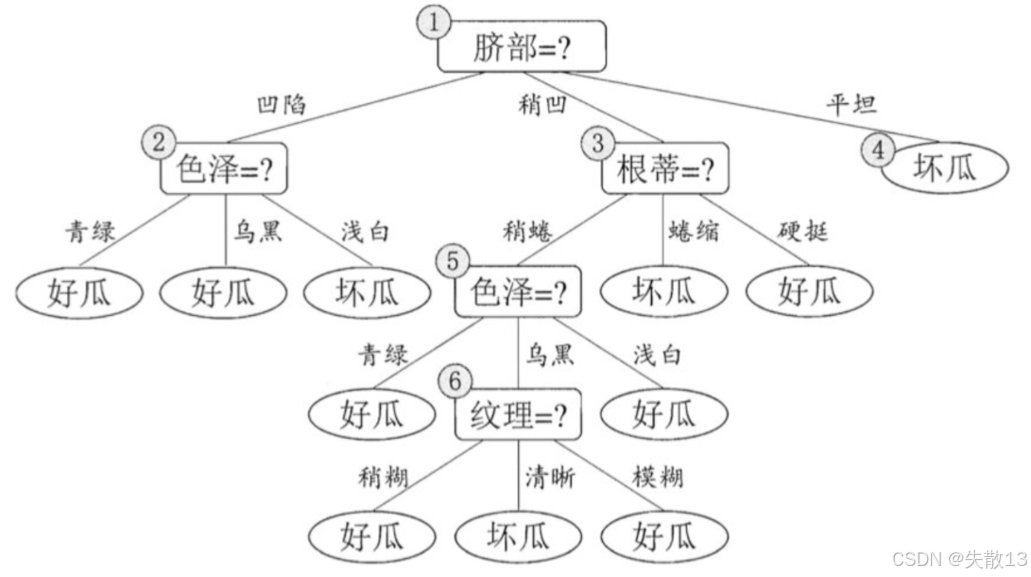
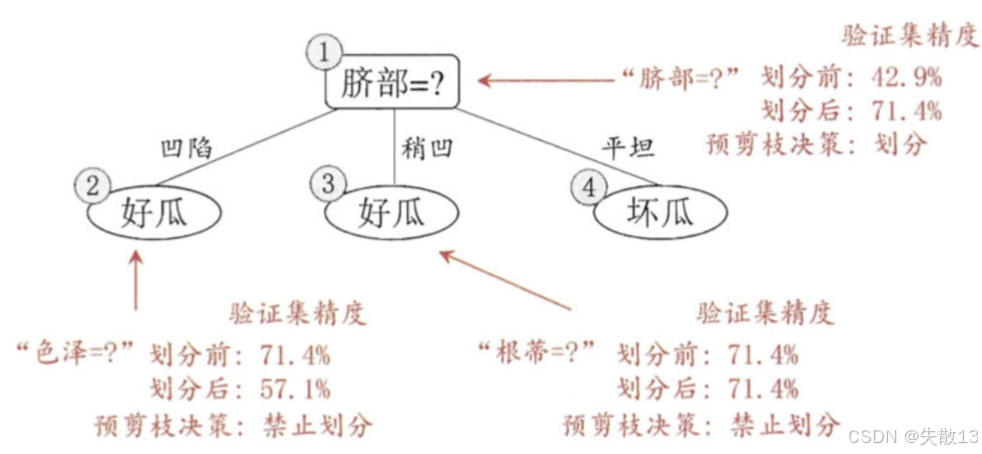
  • 预剪枝：预剪枝在决策树生成过程中，对每个节点在划分前进行估计，若当前节点的划分不能带来泛化性能的提升，则停止划分。例如：

    • 在"脐部=?"的划分中，划分前的验证集精度为42.9%，划分后的验证集精度为71.4%，因此预剪枝决策为划分
    • 而在"色泽=?"和"根蒂=?"的划分中，划分后的验证集精度下降或不变，因此预剪枝决策为禁止划分；

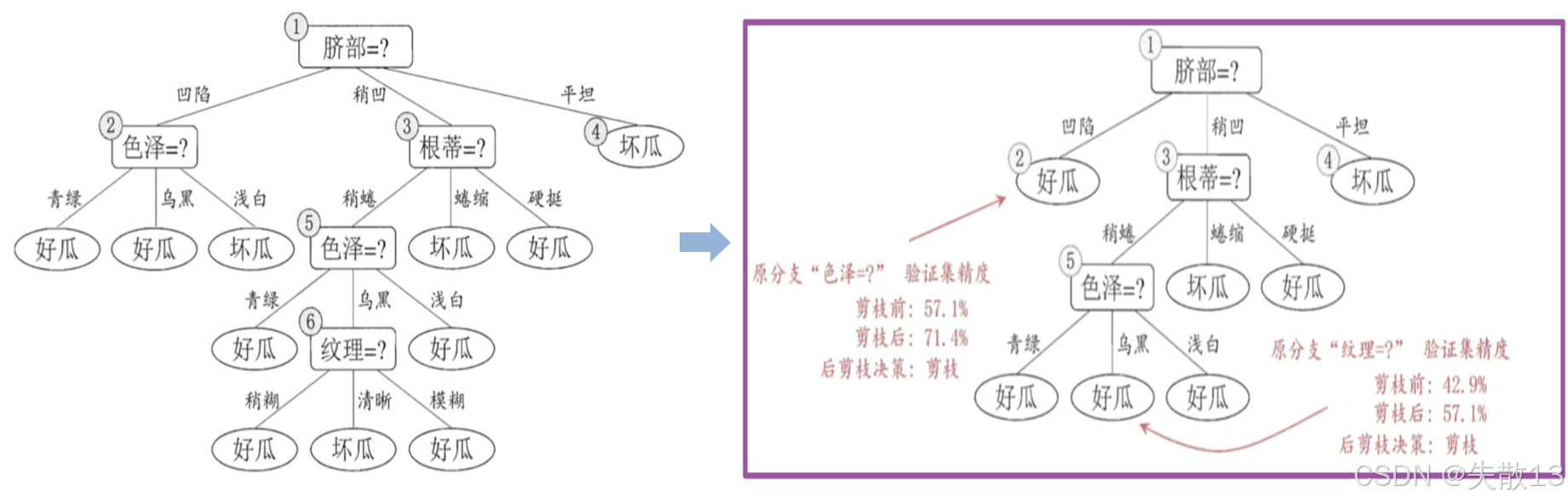
  • 后剪枝：后剪枝先从训练集生成一棵完整的决策树，然后自底向上地对非叶节点进行考察。若将该节点对应的子树替换为叶节点能带来泛化性能的提升，则将该子树替换为叶节点。例如：

    • 在原始分支"色泽=?"的验证集精度为57.1%，剪枝后的验证集精度为71.4%，因此后剪枝决策为剪枝；
    • 在原始分支"纹理=?"的验证集精度为42.9%，剪枝后的验证集精度为57.1%，因此后剪枝决策为剪枝；

  • 剪枝技术对比

    剪枝技术 优点 缺点
    预剪枝 使决策树的很多分支没有展开，不仅降低了过拟合风险，还显著减少了决策树的训练、测试时间开销 有些分支的当前划分虽不能提升泛化性能，但后续划分却有可能导致性能的显著提高；预剪枝决策树也带来了欠拟合的风险
    后剪枝 比预剪枝保留了更多的分支。一般情况下，后剪枝决策树的欠拟合风险很小，泛化性能往往优于预剪枝 后剪枝先生成，后剪枝。自底向上地对树中所有非叶子节点进行逐一考察，训练时间开销比未剪枝的决策树和预剪枝的决策树都要大得多
热门推荐
01全球最强模型Grok4，国内已可免费使用！（附教程）02UV安装并设置国内源03Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code04[已解决]VSCode右键菜单消失恢复05🚀Cursor CLI+GPT-5保姆级教程+编程能力测评！Cursor CLI零成本免费使用GPT-5！Claude Code的劲敌来了！从安装到实战演示06GPT-5 使用限制与国内升级全攻略（免费 / Plus / Pro）【2025 最新】072025最新国内服务器可用docker源仓库地址大全（2025年8月更新）08KGG转MP3工具|非KGM文件|解密音频09Cursor 终端“卡死/无响应”问题的解法10OpenAI重返开源！GPT-OSS本地部署完全指南