preface
今天加油,争取学两节强化课。这是第一节。
odd number and even number
求高阶导数可以利用函数的奇偶性。

判断出来 f(x)=g(x)+g(−x)f(x)=g(x)+g(-x)f(x)=g(x)+g(−x) 是偶函数,周期是 2π2\pi2π, 导数的周期和原来函数的周期是一致的,所以 f′′′(2π)=f′′′(0)f'''(2\pi)=f'''(0)f′′′(2π)=f′′′(0) ,偶函数求导是奇函数,奇函数求导是偶函数,如此得到 f′′′(x)f'''(x)f′′′(x) 是奇函数,所以答案是零。
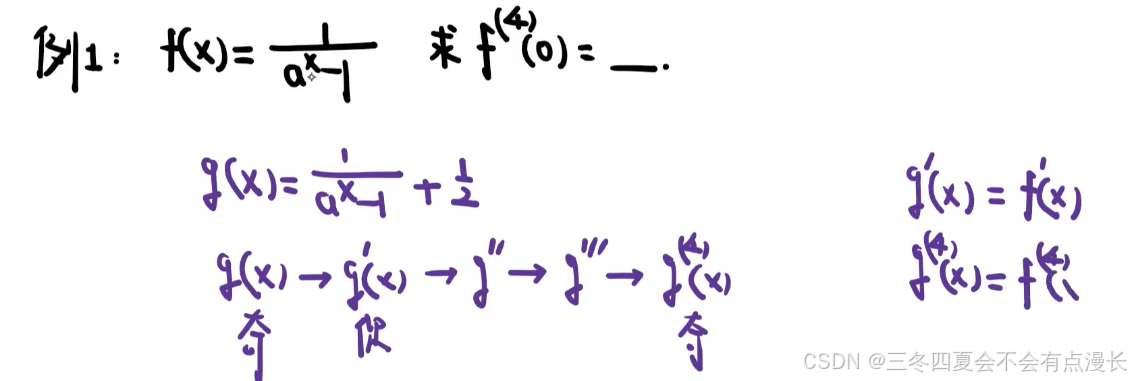
这题可以作为奇偶性的补充。就是我们怎么构造出来一个奇函数,然后用高阶导数的奇偶性来做题,实际上也不需要构造奇函数,构造偶函数也是可以的。关键是最后那个高阶导数能不能落到奇函数,因为一般考察就考察奇函数在 0 处为 0,所以常见的奇函数、偶函数可以积累一下。
常见的奇函数:1ax−1+12,f(x+y)=f(x)+f(y),f(x)是奇函数,arcsinx,tanx,sinx,arctanx,ex−e−x2,ln(x+1+x2),12x+1−12,et−1et+1\frac{1}{a^x-1}+\frac12,f(x+y)=f(x)+f(y),f(x) 是奇函数,\arcsin x,\tan x,\sin x, \arctan x,\frac{e^x-e^{-x}}{2},\ln ({x+\sqrt {1+x^2}}),\frac 1{2^x+1}-\frac12,\frac{e^t-1}{e^t+1}ax−11+21,f(x+y)=f(x)+f(y),f(x)是奇函数,arcsinx,tanx,sinx,arctanx,2ex−e−x,ln(x+1+x2 ),2x+11−21,et+1et−1
常见的偶函数 cosx,ex+e−x2(悬链线)\cos x, \frac{e^x+e^{-x}}{2}(悬链线)cosx,2ex+e−x(悬链线)
67 intensify
重复到极致就是高手。这题可以用奇偶性来做,判断出来原来的函数是偶函数,一阶导奇函数,二阶偶函数,三阶奇函数,然后在零处就是零。所以也别刷 1000 和 660 了,吃透做过的题,比啥都重要。
泰勒,实际操作起来还是有一些难度的,所以眼过千遍,不如手过一遍。加油。感觉有章法一点,扎实一点。比较稳一点。加油。感觉自己为了进度的话,可以不做 800 暂时。反正刷题就是为了提升熟练度呗。虽然我知道有好处,但是往后面拖一拖也没有任何问题,毕竟我现在讲义也没有完全吃透呢。还要追讲义的进度。等讲义的进度全部追完,再不紧不慢地刷题,可能效果要好得多呢。确实是这样。所以加油。我现在学到专题 9,课程更新到了 27,大概差了十几天的进度吧。但是没事的。等线代开始,我一定要努力跟着线代的进度,然后再复习高数的部分,然后概率的基础和强化一块过一遍。反正时间充裕。我一定是可以的。
问到何时葡萄先成熟,你要静候再静候。我到时候考研上岸了,发朋友圈就用这条文案。我太喜欢这种有意思的句子了。感觉意思就是要积累沉淀一段时间。高阶导数是每年五分题的常考点。这块就是,公式法,奇偶性,递归找规律归纳,泰勒,就是四种方法。

intensify 68
这题首先是一个诱敌深入,让我们算 3 阶导数,实际上算 3 阶导数应该算是高阶导数了,硬求导有点傻了。高阶导数,公式,奇偶,递归,泰勒,这题选用泰勒,然后系数对应就可以解决了。没啥难度。
intensify 69
方法 1:用 Leibnitz 公式,加上公式法,我感觉公式有点难记呀。我印象很深刻,3 月份的时候有个朋友问我这个题,我当时用公式法给他解释,但是我不记得公式,我到现在公式都不记得,但是没关系,今天之后不断记忆这个公式,考试的时候记得就可以了。[1ax+b](n)=(−1)nann!(ax+b)n+1[\frac{1}{ax+b}]^{(n)}=\frac{(-1)^na^{n}n!}{(ax+b)^{n+1}}[ax+b1](n)=(ax+b)n+1(−1)nann!
method 2: Taylor ,用泰勒的话,要注意展开到一个一般的项,所以我们一般那个通项公式最好也是记住的。泰勒公式,绝对的考试重点。
supplement
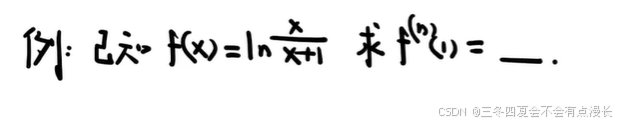

假设不是求零处的高阶导数,可以考虑换元法。然后中间凑我们常见的初等函数的那一步,也是非常精彩。所以数学高分确实厉害,因为考研数学里面确实很多细节,我认为数学高分至少可以说明这个同学花费了很多的时间和精力研究这些具体的问题。很能说明一个人的学习能力。我考上之后这辈子都不想再碰考研数学了哈哈哈。这题也不违背我们积累的经验,就是遇到对数函数,就把真数拆开。对数函数我们想要展开,比较喜欢这种形式:ln(1+x)\ln {(1+x)}ln(1+x) 。感觉我适合把一套资料反复刷,直到吃透为止。关键的资料反复刷,比刷很多套资料感觉更有用一点。算了,就是把讲义吃透就完事了。讲义,真题,模拟卷。就真的足够了。真题有 17 年的,然后模拟卷可以做的有 43 套,这个训练量也挺大的了。60 * 20 = 1200,也差不多有一千道题,完全吃透也可以上考场了。给自己的压力小一点,这么看数学还是很有希望的,要有信心。边际效应也很明显,实在不行就降低一些目标,让其他部分尽量多拿一些分数,最后能上岸,其实就算达到目标了。具体考多少分,实际上不那么重要。关键是总分要上去。唯一的评价标准是总分要上去。
intensify 70
这题是,切线方程,我感觉自己这块基本不可能出错,算的时候,最好每行就写一个式子,这样思路更加流畅,就像写代码一样。
intensify 71
这题就是凑一个导数定义就结束了。非常非常简单。思路还是很明确吧,就是把讲义刷完之后就结束了。考研是比拼质量的,不是来干活的!!!这和健身一样,动作质量比容量要关键很多,虽然容量也是有作用的,但是边际效应非常明显。
今天只能学到这里了,没有学完的部分明天再学。问到何时葡萄先熟透,你要静候再静候。