这是我在我的网站中截取的文章,有更多的文章欢迎来访问我自己的博客网站rn.berlinlian.cn,这里还有很多有关计算机的知识,欢迎进行留言或者来我的网站进行留言!!!
一、逻辑回归代价函数的定义
逻辑回归的代价函数 (又称交叉熵损失)用于评估模型预测结果与真实标签之间的差异。不同于线性回归的均方误差,它专门针对分类问题设计,能够有效惩罚"高置信度的错误预测",同时鼓励模型输出更接近真实标签的概率值。
通俗理解
想象老师在批改判断题:
如果学生非常自信地答错(比如写"绝对选A",但正确答案是B),老师会狠狠扣分。
如果学生答对但不太确定(比如写"可能是A"),老师会适当给分。
如果学生答对且很确定 (比如写"肯定选A"),老师会给满分。
代价函数的作用类似------让模型为自己的"盲目自信"付出代价,同时奖励正确且确定的预测。
二、平方误差 vs 逻辑回归:代价函数的设计差异与凸性对比
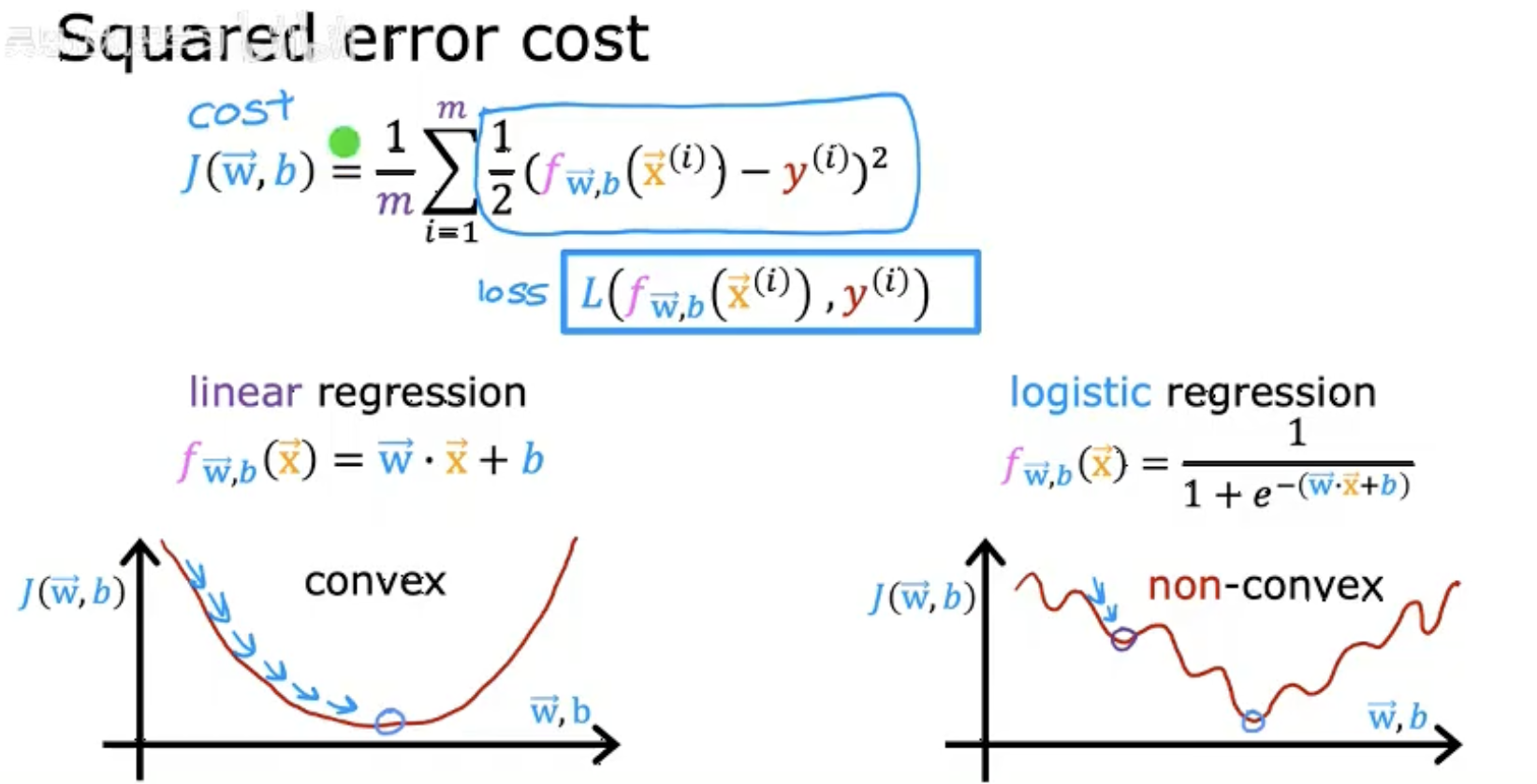
这张图片展示了平方误差代价函数(Squared error cost)及其相关概念,主要分为以下几个部分:
-
平方误差代价函数公式:
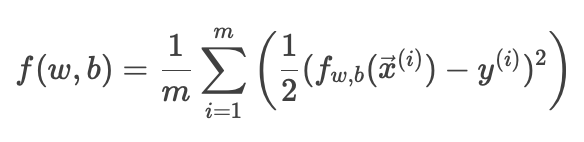
用于衡量线性回归模型的预测值与真实值之间的误差。
-
损失函数(loss):
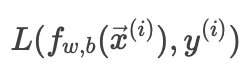
表示单个样本的误差。
-
线性回归模型:
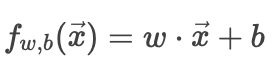
这是一个线性预测函数。
-
凸性与非凸性:
-
线性回归的代价函数 f(w,b) 是凸函数(convex),保证梯度下降能找到全局最优解。
-
如果直接对逻辑回归使用平方误差,代价函数可能非凸(non-convex),导致优化困难。
-
-
逻辑回归的预测函数:
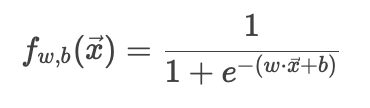
这是一个Sigmoid函数,将线性输出映射到概率(0, 1)。
图片的核心对比了线性回归(平方误差) 和**逻辑回归(需用交叉熵损失)**在代价函数设计上的差异。
三、逻辑回归代价函数公式
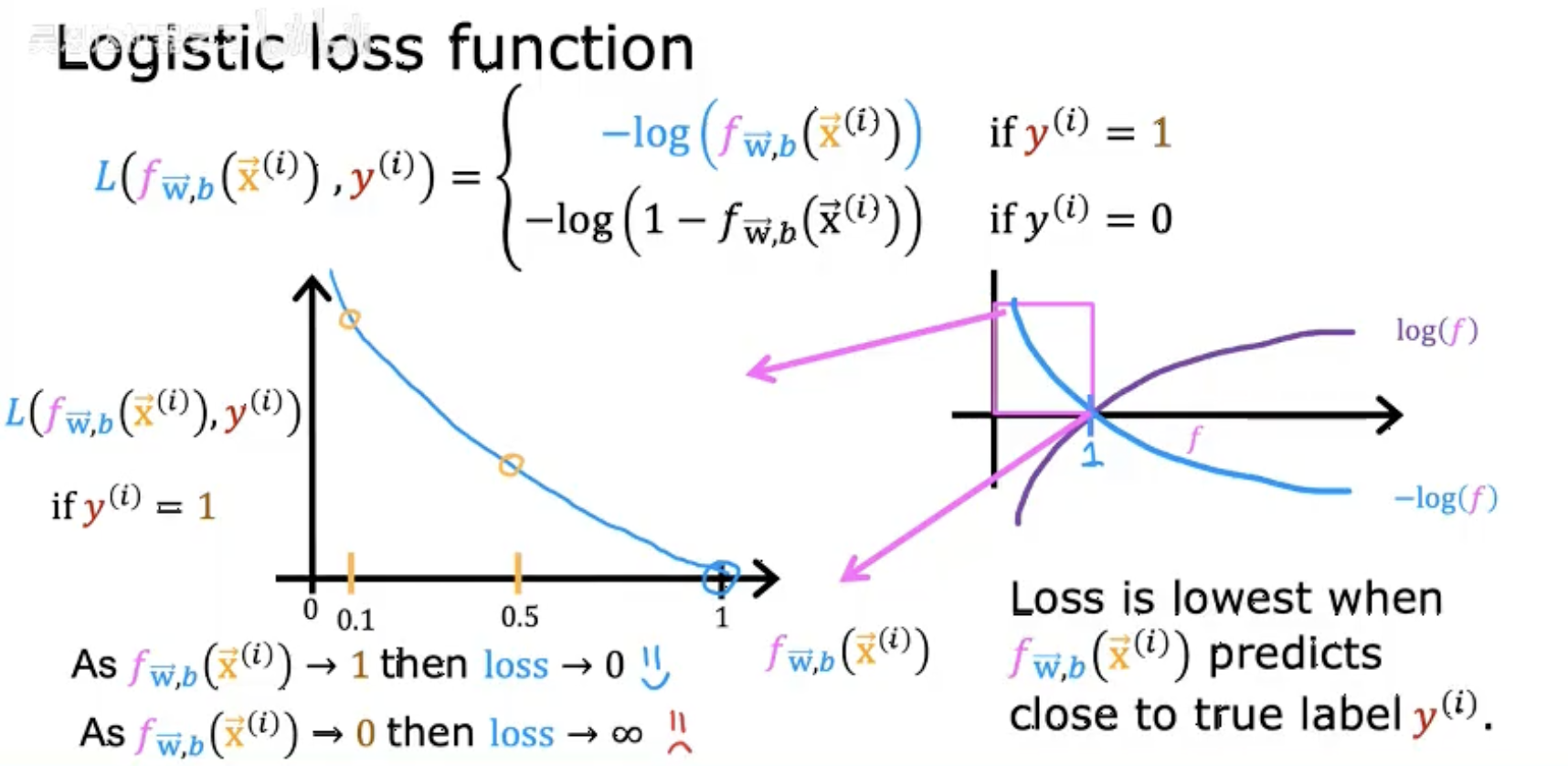
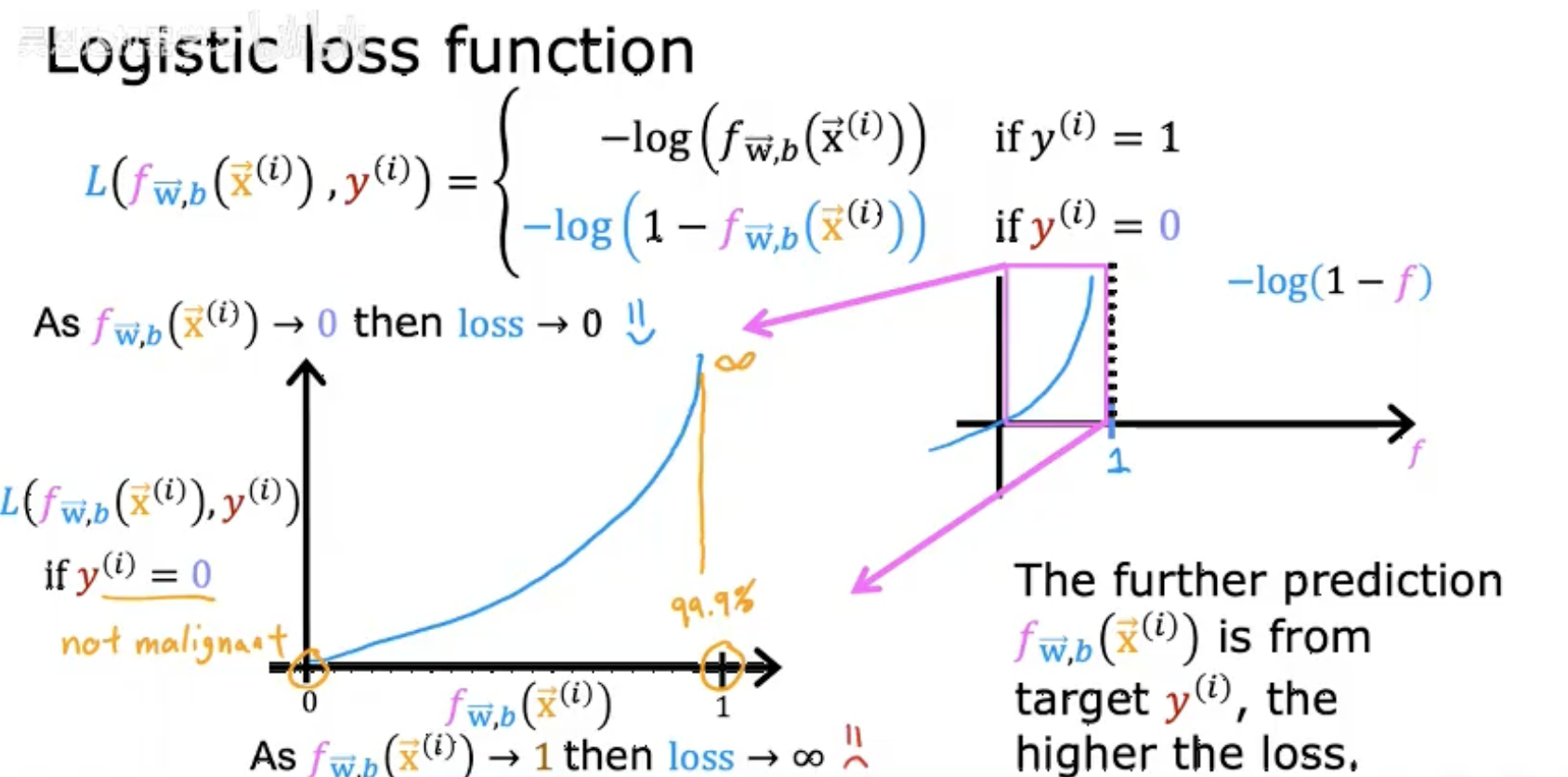
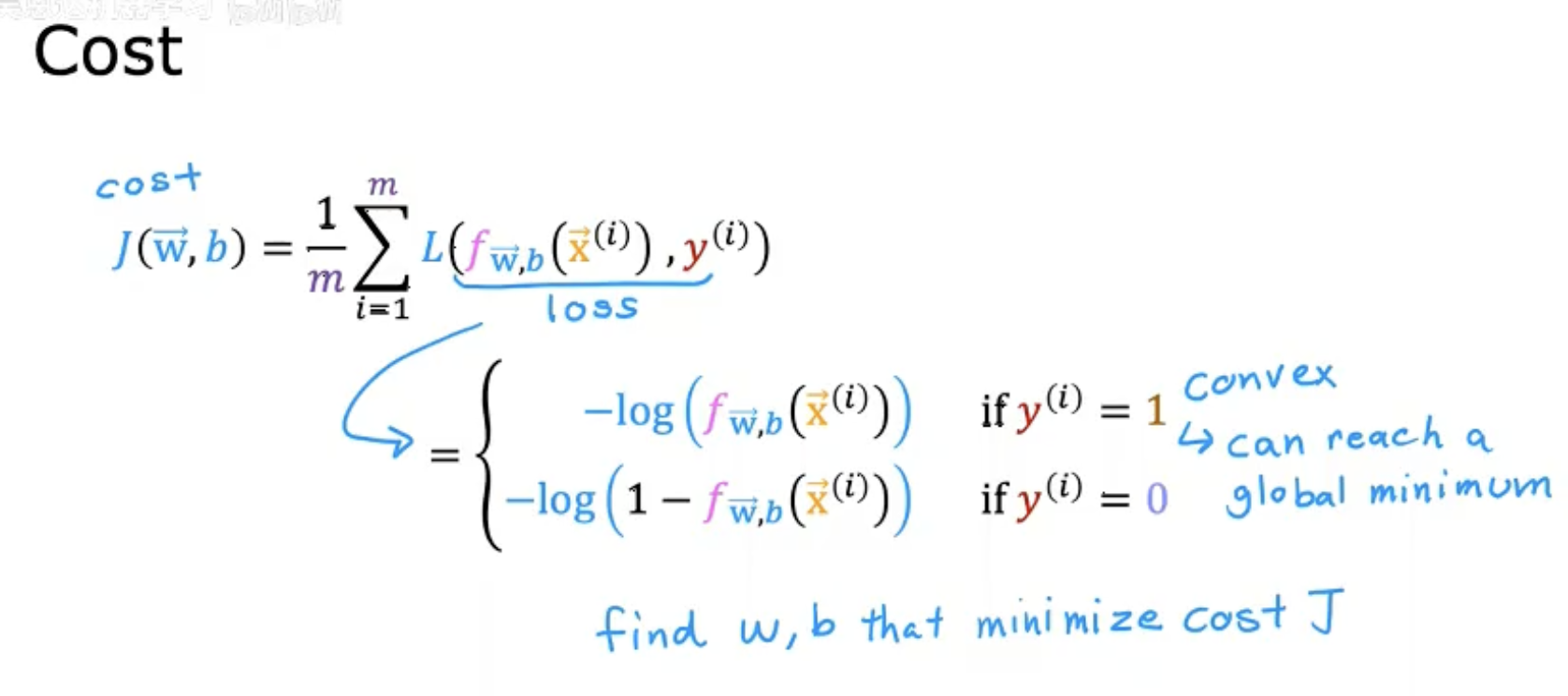
-
分段定义 :
损失函数 L 根据真实标签 y(i) 的取值(0 或 1)分段计算:
-
若 y(i)=1,损失为 −log(fW,b(x⃗(i)))。
-
若 y(i)=0,损失为 −log(1−fW,b(x⃗(i)))。
-
-
损失变化趋势:
-
当预测值 fW,b(x⃗(i)) 接近真实标签时(如 y(i)=1 且 f→1),损失趋近于 0。
-
当预测值与真实标签相反时(如 y(i)=1 但 f→0),损失趋近于无穷大。
-
-
核心作用 :
损失函数通过对数惩罚机制,迫使模型对错误预测(尤其是高置信度错误)付出更高代价,从而推动参数优化。
-
优化目标
通过调整参数 w⃗,b 最小化代价函数 J,使模型预测 fw⃗,b(x⃗) 尽可能接近真实标签 y。
四、逻辑回归损失函数的两种表达形式及其统一化


-
第一幅图
-
展示了逻辑回归损失函数从分段形式 到统一形式的简化过程。
-
分段形式(直观但冗长):
-
当 y=1,损失为 −log(f(x))
-
当 y=0,损失为 −log(1−f(x))
-
-
统一形式(紧凑且通用):
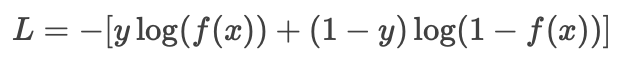
-
通过数学技巧将两种情况合并为一个公式,便于计算和优化。
-
-
第二幅图
-
将单样本的损失函数推广到整体代价函数(所有样本的平均损失)。
-
公式:
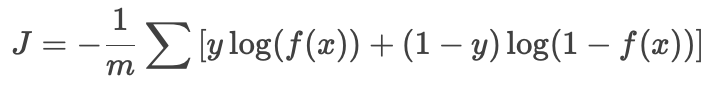
-
强调该函数是凸函数(convex),保证梯度下降能找到全局最优解。
-
这是我在我的网站中截取的文章,有更多的文章欢迎来访问我自己的博客网站rn.berlinlian.cn,这里还有很多有关计算机的知识,欢迎进行留言或者来我的网站进行留言!!!