今天我打算重写深度优先搜索(DeepSeek)(huaji)和广度优先搜索了,之前写的实在太烂啦,所以大家准备好纸和笔,一起来听听下面博主的讲解的吧
注:如果有写的不好的地方,那么请各位指出,但是请不要恶意攻击,不然后果自负
深度优先搜索(DFS)
前言
深度优先搜索(DFS)是一种很重要很重要的算法,后面学到图论,其中很多算法就是以深度优先搜索为底子的(如Tarjan),所以大家需要认真学习这个算法,为以后的学习打下牢固的基础(水字数的老毛病又犯了哈哈哈)
底层逻辑
不知道大家平时有没有玩过迷宫?玩过的同学又是怎么去找出路线的呢(博主都是一眼都就看出来的哈哈哈),那么计算机没有这种一眼下去就有大概路线的方法,计算机又是怎么逛迷宫的呢,计算机会使用搜索算法,深度优先搜索(以下简称DFS)是很有名的一种,DFS在空间时间方面不占优势(个人觉得比广搜慢一点,空间占用大一点),但是凭它那简洁的代码、那通俗易懂的思路和他那容易爆栈的危险(是不是不应该在这说哈哈)仍然广受大家欢迎,那他是怎么运作的呢?
现在想象一个迷宫(木有灯),深度优先搜索的工作原理就是:先朝一个方向尝试,然后有两种可能性,一种是一头撞墙上,另一种就是走进了一条路(也有可能还是这条,毕竟路也会拐弯),如果是第一种情况,那么就朝下个方向干同样的事情,如果所有方向都尝试过了,那么就退回上一步,如果是第二种情况,那么就进入那个新的点继续尝试,尝试完了就回到上一个点(如果走到终点就看看题目,如果只要你走到不管步数或类似的东西就直接结束,要管的话还要退回去,所以在每次走进新路的时候都要计算步数),如果都尝试完了(也就是跑回起点了)那么就可以结束了。
这个就是DFS的底层思路,撞遍所有的墙,走遍所有的路,找到路了就一路走到黑,撞晕了在回去上一个地方
实现方式
前置知识
如果你想学习DFS的实现方式,那么你得会递归,不会递归的请去自己学习(博主光讲搜索就很累了明明就是不想写),递归还是很简单的,基本一学就会
正题
咳咳咳,那么我现在就要开始讲讲DFS的具体实现方式了,既然看到这里的都学过递归,那么请看看DFS为什么那么适合用递归呢,大家知道,递归是可以回溯的,根本不需要什么记录上个点,这个就完美符合了DFS对于回溯的要求,还有,递归那种"一路走到黑"的特性也完美符合DFS的要求。
那么我们对于递归那么了解,也就不用废话解释了,直接上代码!
cpp
int DFS(int x,int y,int step){//x,y为坐标、step为步数(这项视题目而定,如果题目不求最短路,就可以不用他)
if(mapp[x][y]==0)return -1;
//mapp为地图,每个点0为墙,1为路,2为终点,-1表示此路不通
if(mapp[x][y]==2) return step; //如果只问有没有路,直接返回1即可
mapp[x][y]=0;//防止走回头路
int p=min(DFS(x+1,y,step+1),min(DFS(x-1,y,step+1),min(DFS(x,y+1,step+1),DFS(x,y-1,step+1))));//如果只问有没有路,就判断一下前面返回有没有一,有就返回1就可以了
mapp[x][y]=1;
return p;
}例题
(题目来源于洛谷)
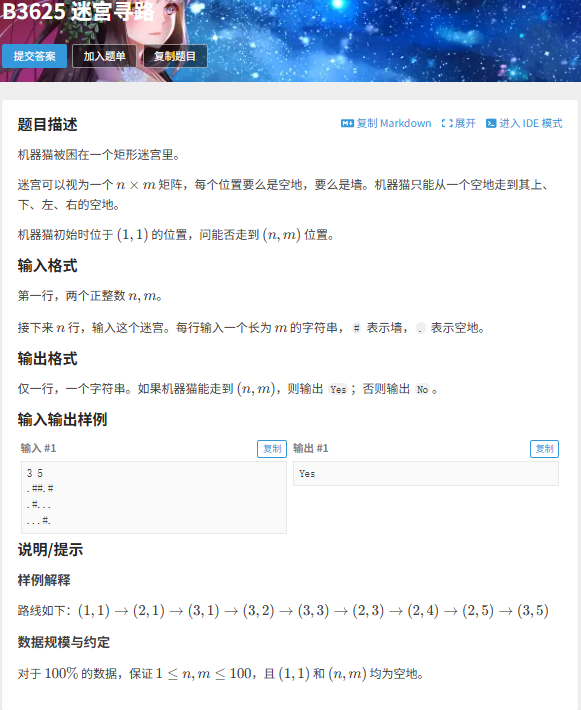
那这道题就很很很很很模板了,只要DFS一波,到终点返回1即可, 代码的话就在上面的模版那里,按注释里说的稍加变化即可
广度优先搜索(BFS)
底层逻辑
就不废话了(想解放qwq),直接开讲(又废话了一波)
比起DFS的单线程搜索,BFS就比较厉害了,他是这样的,还是个迷宫,但是呢,BFS就是直接往里面倒桶水(水源无限)如果然后到终点记录时间(水每秒走一格),如果水流出来了,那么迷宫就有路可走,时间就是你记录的时间。(更快了)
实现方式
既然更快,那么代码一定复杂(我这里就不写了),代码逻辑是这样的:首先建一个队列,往队列里摁入起点坐标(可以用pair,也可以用struct自定义),然后去找队里面的元素的相邻节点一一入队(先统计原队列里有多少个数据,在去出相应的数据,就不会出现新进来的就被出出去的情况了),每一步计算时间,到终点就跳出循环,输出数据,就是这么简单。
后记
重制一片真不容易呀,后面我会慢慢完善的