[机器学习]08-基于逻辑回归模型的鸢尾花数据集分类

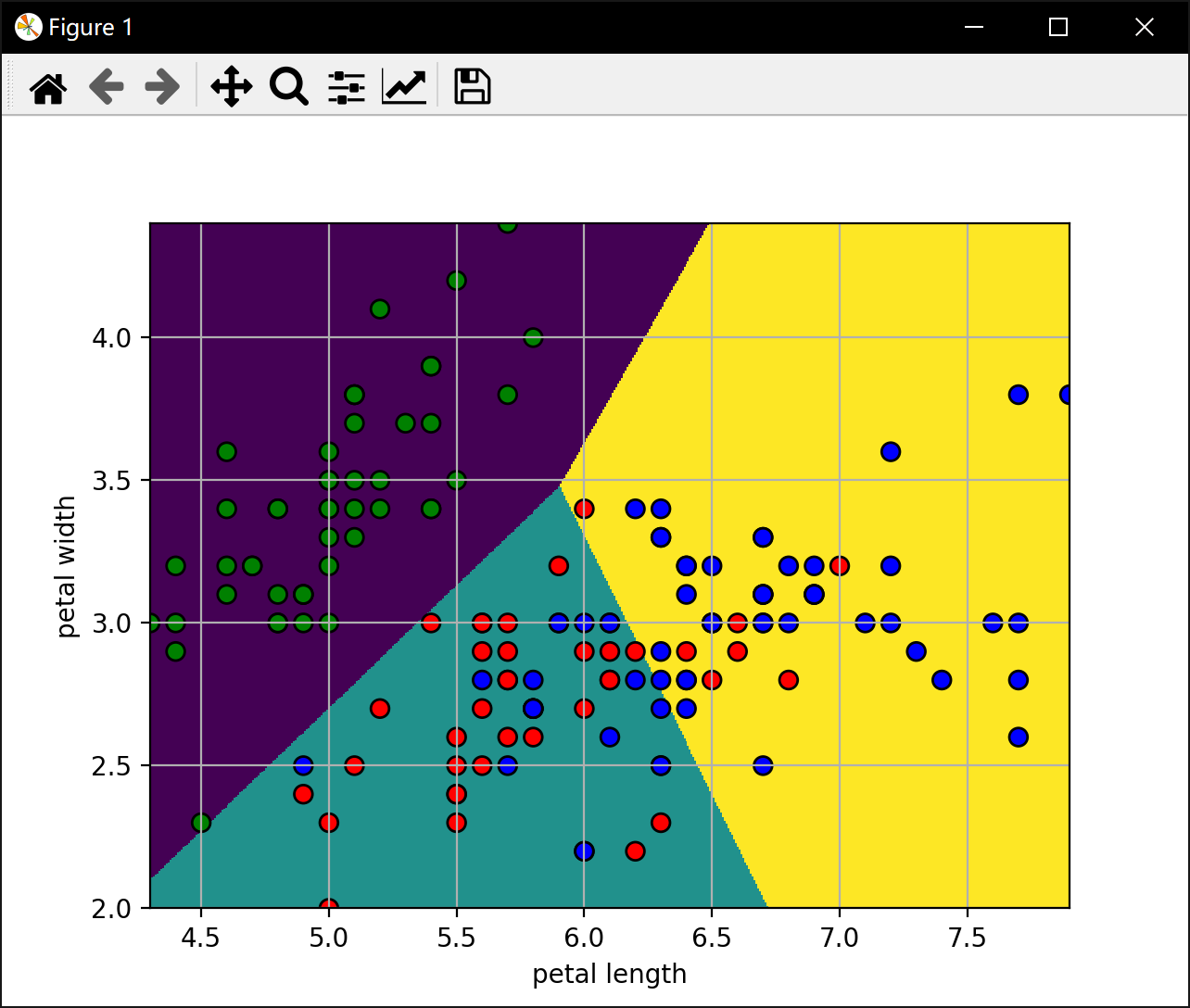
使用sklearn的LogisticRegression多分类模型

程序代码：

python 复制代码

import numpy as np
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn import datasets
from sklearn import preprocessing
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline

df = pd.read_csv('http://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=0)
x = df.values[:, :-1]
y = df.values[:, -1]
print('x = \n', x)
print('y = \n', y)
le = preprocessing.LabelEncoder()
le.fit(['Iris-setosa', 'Iris-versicolor', 'Iris-virginica'])
print(le.classes_)
y = le.transform(y)
print('Last Version, y = \n', y)

x = x[:, 0:2]
print(x)
print(y)
#x = StandardScaler().fit_transform(x)
lr = LogisticRegression()   # Logistic回归模型
lr.fit(x, y.ravel())        # 根据数据[x,y]，计算回归参数

X = x
Y = y
N, M = 500, 500     # 横纵各采样多少个值
x1_min, x1_max = X[:, 0].min(), X[:, 0].max()   # 第0列的范围
x2_min, x2_max = X[:, 1].min(), X[:, 1].max()   # 第1列的范围
t1 = np.linspace(x1_min, x1_max, N)
t2 = np.linspace(x2_min, x2_max, M)
x1, x2 = np.meshgrid(t1, t2)                    # 生成网格采样点
x_test = np.stack((x1.flat, x2.flat), axis=1)   # 测试点
print(x_test)

cm_light = mpl.colors.ListedColormap(['#009933', '#ff6666', '#33ccff'])
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
y_hat = lr.predict(x_test)       # 预测值
y_hat = y_hat.reshape(x1.shape)                 # 使之与输入的形状相同
plt.pcolormesh(x1, x2, y_hat)     # 预测值的显示
plt.scatter(X[:, 0], X[:, 1], c=Y.ravel(), edgecolors='k', s=50, cmap=cm_dark)
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.grid()
plt.show()

运行结果：

x =
$\[4.9 3.0 1.4 0.2$ $4.7 3.2 1.3 0.2$ $4.6 3.1 1.5 0.2$ $5.0 3.6 1.4 0.2$ $5.4 3.9 1.7 0.4$ $4.6 3.4 1.4 0.3$ $5.0 3.4 1.5 0.2$ $4.4 2.9 1.4 0.2$ $4.9 3.1 1.5 0.1$ $5.4 3.7 1.5 0.2$ $4.8 3.4 1.6 0.2$ $4.8 3.0 1.4 0.1$ $4.3 3.0 1.1 0.1$ $5.8 4.0 1.2 0.2$ $5.7 4.4 1.5 0.4$ $5.4 3.9 1.3 0.4$ $5.1 3.5 1.4 0.3$ $5.7 3.8 1.7 0.3$ $5.1 3.8 1.5 0.3$ $5.4 3.4 1.7 0.2$ $5.1 3.7 1.5 0.4$ $4.6 3.6 1.0 0.2$ $5.1 3.3 1.7 0.5$ $4.8 3.4 1.9 0.2$ $5.0 3.0 1.6 0.2$ $5.0 3.4 1.6 0.4$ $5.2 3.5 1.5 0.2$ $5.2 3.4 1.4 0.2$ $4.7 3.2 1.6 0.2$ $4.8 3.1 1.6 0.2$ $5.4 3.4 1.5 0.4$ $5.2 4.1 1.5 0.1$ $5.5 4.2 1.4 0.2$ $4.9 3.1 1.5 0.1$ $5.0 3.2 1.2 0.2$ $5.5 3.5 1.3 0.2$ $4.9 3.1 1.5 0.1$ $4.4 3.0 1.3 0.2$ $5.1 3.4 1.5 0.2$ $5.0 3.5 1.3 0.3$ $4.5 2.3 1.3 0.3$ $4.4 3.2 1.3 0.2$ $5.0 3.5 1.6 0.6$ $5.1 3.8 1.9 0.4$ $4.8 3.0 1.4 0.3$ $5.1 3.8 1.6 0.2$ $4.6 3.2 1.4 0.2$ $5.3 3.7 1.5 0.2$ $5.0 3.3 1.4 0.2$ $7.0 3.2 4.7 1.4$ $6.4 3.2 4.5 1.5$ $6.9 3.1 4.9 1.5$ $5.5 2.3 4.0 1.3$ $6.5 2.8 4.6 1.5$ $5.7 2.8 4.5 1.3$ $6.3 3.3 4.7 1.6$ $4.9 2.4 3.3 1.0$ $6.6 2.9 4.6 1.3$ $5.2 2.7 3.9 1.4$ $5.0 2.0 3.5 1.0$ $5.9 3.0 4.2 1.5$ $6.0 2.2 4.0 1.0$ $6.1 2.9 4.7 1.4$ $5.6 2.9 3.6 1.3$ $6.7 3.1 4.4 1.4$ $5.6 3.0 4.5 1.5$ $5.8 2.7 4.1 1.0$ $6.2 2.2 4.5 1.5$ $5.6 2.5 3.9 1.1$ $5.9 3.2 4.8 1.8$ $6.1 2.8 4.0 1.3$ $6.3 2.5 4.9 1.5$ $6.1 2.8 4.7 1.2$ $6.4 2.9 4.3 1.3$ $6.6 3.0 4.4 1.4$ $6.8 2.8 4.8 1.4$ $6.7 3.0 5.0 1.7$ $6.0 2.9 4.5 1.5$ $5.7 2.6 3.5 1.0$ $5.5 2.4 3.8 1.1$ $5.5 2.4 3.7 1.0$ $5.8 2.7 3.9 1.2$ $6.0 2.7 5.1 1.6$ $5.4 3.0 4.5 1.5$ $6.0 3.4 4.5 1.6$ $6.7 3.1 4.7 1.5$ $6.3 2.3 4.4 1.3$ $5.6 3.0 4.1 1.3$ $5.5 2.5 4.0 1.3$ $5.5 2.6 4.4 1.2$ $6.1 3.0 4.6 1.4$ $5.8 2.6 4.0 1.2$ $5.0 2.3 3.3 1.0$ $5.6 2.7 4.2 1.3$ $5.7 3.0 4.2 1.2$ $5.7 2.9 4.2 1.3$ $6.2 2.9 4.3 1.3$ $5.1 2.5 3.0 1.1$ $5.7 2.8 4.1 1.3$ $6.3 3.3 6.0 2.5$ $5.8 2.7 5.1 1.9$ $7.1 3.0 5.9 2.1$ $6.3 2.9 5.6 1.8$ $6.5 3.0 5.8 2.2$ $7.6 3.0 6.6 2.1$ $4.9 2.5 4.5 1.7$ $7.3 2.9 6.3 1.8$ $6.7 2.5 5.8 1.8$ $7.2 3.6 6.1 2.5$ $6.5 3.2 5.1 2.0$ $6.4 2.7 5.3 1.9$ $6.8 3.0 5.5 2.1$ $5.7 2.5 5.0 2.0$ $5.8 2.8 5.1 2.4$ $6.4 3.2 5.3 2.3$ $6.5 3.0 5.5 1.8$ $7.7 3.8 6.7 2.2$ $7.7 2.6 6.9 2.3$ $6.0 2.2 5.0 1.5$ $6.9 3.2 5.7 2.3$ $5.6 2.8 4.9 2.0$ $7.7 2.8 6.7 2.0$ $6.3 2.7 4.9 1.8$ $6.7 3.3 5.7 2.1$ $7.2 3.2 6.0 1.8$ $6.2 2.8 4.8 1.8$ $6.1 3.0 4.9 1.8$ $6.4 2.8 5.6 2.1$ $7.2 3.0 5.8 1.6$ $7.4 2.8 6.1 1.9$ $7.9 3.8 6.4 2.0$ $6.4 2.8 5.6 2.2$ $6.3 2.8 5.1 1.5$ $6.1 2.6 5.6 1.4$ $7.7 3.0 6.1 2.3$ $6.3 3.4 5.6 2.4$ $6.4 3.1 5.5 1.8$ $6.0 3.0 4.8 1.8$ $6.9 3.1 5.4 2.1$ $6.7 3.1 5.6 2.4$ $6.9 3.1 5.1 2.3$ $5.8 2.7 5.1 1.9$ $6.8 3.2 5.9 2.3$ $6.7 3.3 5.7 2.5$ $6.7 3.0 5.2 2.3$ $6.3 2.5 5.0 1.9$ $6.5 3.0 5.2 2.0$ $6.2 3.4 5.4 2.3$ $5.9 3.0 5.1 1.8\]$
y =
$'Iris-setosa' 'Iris-versicolor' 'Iris-virginica'$
Last Version, y =
$0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2$ $\[4.3 2.$ $4.30721443 2.$ $4.31442886 2.$
...
$7.88557114 4.4$ $7.89278557 4.4$ $7.9 4.4 \]$
进程已结束,退出代码0