2025-08-16：将元素分配给有约束条件的组。用go语言，给定两个整数数组：groups（groups[i] 表示第 i 个组的大小）和 elements。

2025-08-16：将元素分配给有约束条件的组。用go语言，给定两个整数数组：groups（groups[i] 表示第 i 个组的大小）和 elements。对每个组 i，从 elements 中选出一个下标 j（返回的结果是这些下标构成的数组 assigned），满足以下要求：

只能选那些能整除该组大小的元素（即 elements[j] 是 groups[i] 的因子）。
若有多个满足条件的下标，取最小的下标 j。
若没有任何元素满足，则对应位置记为 -1。
同一个元素可以被多个组重复选用。

返回按组顺序得到的下标数组 assigned。

1 <= groups.length <= 100000。

1 <= elements.length <= 100000。

1 <= groups[i] <= 100000。

1 <= elements[i] <= 100000。

输入： groups = [8,4,3,2,4], elements = [4,2]。

输出： [0,0,-1,1,0]。

解释：

elements[0] = 4 被分配给组 0、1 和 4。

elements[1] = 2 被分配给组 3。

无法为组 2 分配任何元素，分配 -1 。

题目来自力扣3447。

分步骤描述过程：

初始化阶段：
- 首先找到 groups 数组中的最大值 mx，这个值决定了我们需要处理的最大组大小。
- 创建一个长度为 mx + 1 的数组 target，并初始化所有值为 -1。target[y] 表示组大小为 y 时选择的 elements 的下标，初始时所有组都未被分配。
预处理阶段（标记阶段）：
- 遍历 elements 数组中的每个元素 x（记其下标为 i）：
  - 如果 x 大于 mx，则跳过（因为没有任何组的大小能比 mx 更大，x 不可能是任何组的因子）。
  - 如果 target[x] 已经被标记（即不为 -1），则跳过（因为我们需要最小的下标，当前 i 比之前标记的下标大）。
  - 对于 x 的所有倍数 y（即 y = x, 2x, 3x, ..., mx）：
    - 如果 target[y] 未被标记（即 -1），则将其标记为 i（表示组大小为 y 时可以选择 elements[i]）。
- 这一步的核心思想是：对于每个 x，标记所有能被 x 整除的组大小 y，并记录最小的 i。
回答询问阶段：
- 遍历 groups 数组中的每个组大小 x：
  - 直接从 target[x] 中获取对应的 elements 下标（因为预处理阶段已经完成了所有可能的标记）。
  - 如果 target[x] 仍为 -1，则表示没有 elements 中的元素能整除 x，分配 -1。
- 将结果直接写入 groups 数组（原地修改）并返回。

示例的具体过程：

以输入 groups = [8,4,3,2,4], elements = [4,2] 为例：

mx = 8，初始化 target = [-1, -1, -1, -1, -1, -1, -1, -1, -1]（长度为 9）。
遍历 elements：
- i=0, x=4：
  - x=4 <= mx，且 target[4] = -1，开始标记：
    - y=4：target[4] = 0。
    - y=8：target[8] = 0。
- i=1, x=2：
  - x=2 <= mx，且 target[2] = -1，开始标记：
    - y=2：target[2] = 1。
    - y=4：target[4] 已经是 0（不更新，因为需要最小下标）。
    - y=6：target[6] = 1。
    - y=8：target[8] 已经是 0（不更新）。
回答询问：
- groups[0]=8：target[8]=0 → 0。
- groups[1]=4：target[4]=0 → 0。
- groups[2]=3：target[3]=-1 → -1。
- groups[3]=2：target[2]=1 → 1。
- groups[4]=4：target[4]=0 → 0。
- 最终结果为 [0, 0, -1, 1, 0]。

时间复杂度：

预处理阶段：
- 遍历 elements 数组：O(m)，其中 m 是 elements 的长度。
- 对于每个 x，标记其倍数 y：总共有 mx/x 次操作。
  - 所有 x 的倍数标记的总次数为 mx/1 + mx/2 + mx/3 + ... + mx/mx ≈ O(mx * log(mx))`（调和级数）。
- 因此预处理阶段的时间复杂度为 O(m + mx * log(mx))。
回答询问阶段：
- 遍历 groups 数组：O(n)，其中 n 是 groups 的长度。
- 因此总时间复杂度为 O(m + mx * log(mx) + n)。

空间复杂度：

target 数组：O(mx)。
其他额外空间：O(1)。
因此总空间复杂度为 O(mx)。

总结：

总时间复杂度：O(m + mx * log(mx) + n)。
总空间复杂度：O(mx)。

其中 mx 是 groups 数组的最大值，m 是 elements 的长度，n 是 groups 的长度。

Go完整代码如下：

go 复制代码

package main

import (
	"fmt"
	"slices"
)

func assignElements(groups []int, elements []int) []int {
	mx := slices.Max(groups)
	target := make([]int, mx+1)
	for i := range target {
		target[i] = -1
	}

	for i, x := range elements {
		if x > mx || target[x] >= 0 { // x 及其倍数一定已被标记，跳过
			continue
		}
		for y := x; y <= mx; y += x { // 枚举 x 的倍数 y
			if target[y] < 0 { // 没有标记过
				target[y] = i // 标记 y 可以被 x 整除（记录 x 的下标）
			}
		}
	}

	// 回答询问
	for i, x := range groups {
		groups[i] = target[x] // 原地修改
	}
	return groups
}


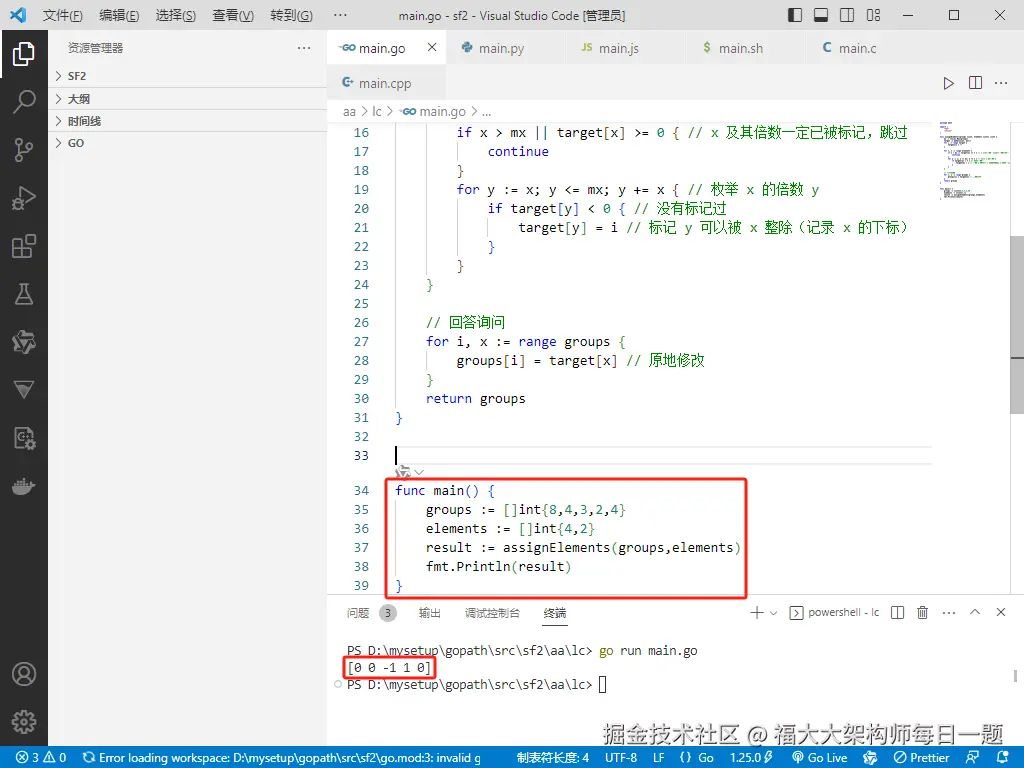
func main() {
	groups := []int{8,4,3,2,4}
	elements := []int{4,2}
	result := assignElements(groups,elements)
	fmt.Println(result)
}

Python完整代码如下：

python 复制代码

# -*-coding:utf-8-*-

from typing import List

def assign_elements(groups: List[int], elements: List[int]) -> List[int]:
    if not groups:
        return []

    mx = max(groups)
    # target[i] = 下标（elements 中的索引），未标记则为 -1
    target = [-1] * (mx + 1)

    for i, x in enumerate(elements):
        if x > mx or target[x] >= 0:
            continue
        y = x
        while y <= mx:
            if target[y] < 0:
                target[y] = i
            y += x

    # 原地修改 groups（如需不修改原列表可创建一个新列表）
    for idx, x in enumerate(groups):
        groups[idx] = target[x] if x <= mx else -1

    return groups

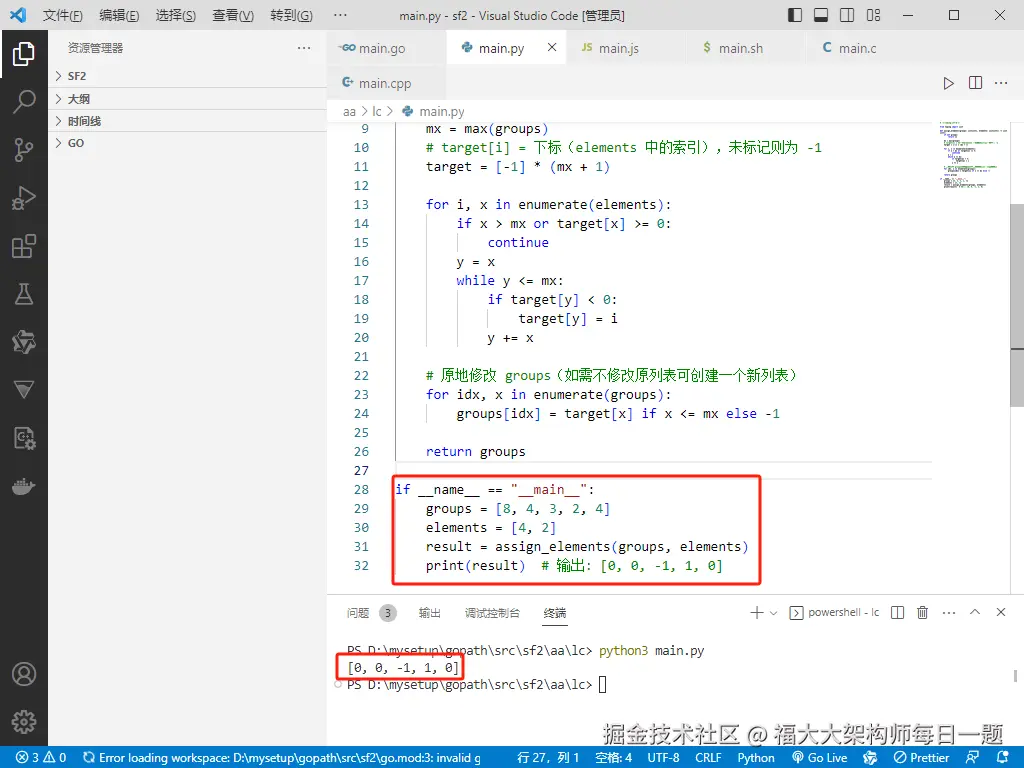
if __name__ == "__main__":
    groups = [8, 4, 3, 2, 4]
    elements = [4, 2]
    result = assign_elements(groups, elements)
    print(result)  # 输出: [0, 0, -1, 1, 0]