在神经网络里,梯度(Gradient) 是一个非常核心的数学概念,它直接决定了模型是如何"学习"的。
🌱 梯度的核心含义
-
数学定义 :梯度是多元函数对各个输入变量的偏导数组成的向量,描述了函数在某一点的变化方向和变化率。
-
几何意义:在某个点上,梯度指向函数值增长最快的方向;梯度的大小表示增长的"陡峭程度"。
🤖 在神经网络中的作用
在神经网络训练时:
-
误差计算 用损失函数(Loss Function)衡量预测值与真实值的差距。
-
梯度求解 通过**反向传播(Backpropagation)**计算损失函数对每个参数(权重和偏置)的梯度。
-
参数更新 使用梯度下降(Gradient Descent)或其变种(Adam、RMSprop 等)按梯度方向调整参数,使损失减小。
🧩 直观理解
想象你在一片雾蒙蒙的山中迷路,海拔高度代表损失值:
-
你想走到最低点(损失最小)。
-
梯度就像你脚下坡度的指南针,告诉你哪个方向是"上坡"。
-
如果想下山,就要沿着梯度的反方向走。
📌 数学符号示例
假设损失函数为 L(w1,w2)L(w_1, w_2),那么梯度是:
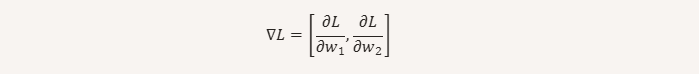
其中每个偏导数表示当改变该参数时,损失变化的速度。