决策树学习

ID3算法

核心指标：信息增益（属性带来的熵增）

划分原则：选择信息增益最大的属性（纯度提升最大）

缺陷：偏好取值较多的属性（如"编号"），易导致过拟合

C4.5算法

信息增益率 = 信息增益 ÷ 自身熵

目的 ：缓解ID3对多值属性的偏好，提升泛化能力

CART算法

核心指标：基尼指数（Gini Index）

公式：Gini(D)=1−∑pi2（p越大，Gini(D)越小，则数据集D的纯度越高）

物理意义 ：随机抽取两个样本类别不一致的概率

划分原则 ：基尼指数越小，数据集纯度越高

连续值处理

方法：通过分箱（离散化）或寻找最佳划分阈值，将连续属性转化为离散值

决策树剪枝策略

预剪枝

边建立决策树边进行剪枝的操作（更实用） · 限制深度，叶子节点个数，叶子节点样本数，信息增益量等。

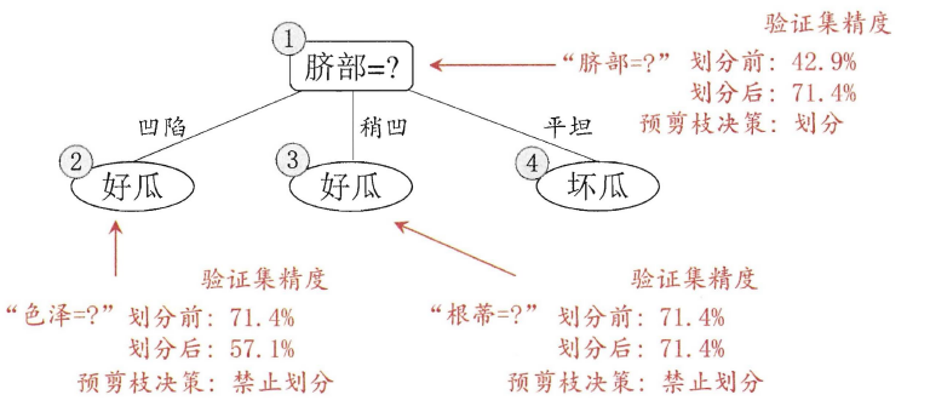
后剪枝

时机：建树完成后进行剪枝

损失函数：最终损失=自身GINI系数+α×叶子节点数量

调节参数 ：α较大 → 抑制过拟合（树更简单）α较小 → 侧重拟合效果（树更复杂）

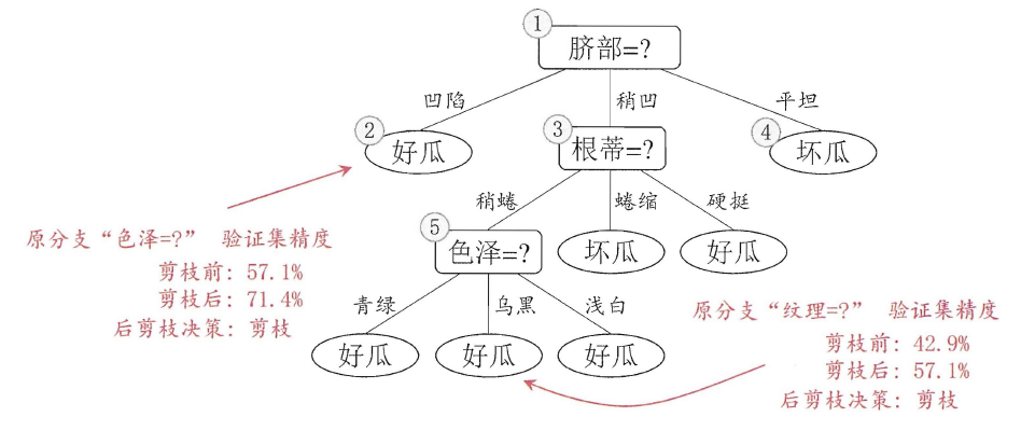
应用举例

泰坦尼克号幸存者预测

python 复制代码

import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
data = pd.read_csv("taitanic_data.csv", index_col = 0)
# 头信息，部分数据信息
data.head()
data.info()
# 删除缺失值过多的列 inplace=True覆盖原表; axis=1 删除列
data.drop(["Cabin"], inplace=True, axis=1)
# 删除和观察判断来说和预测的y没有关系的列
data.drop(["Name", "Ticket"], inplace=True, axis=1)
# 处理缺失值，填充均值
data["Age"] = data["Age"].fillna(data["Age"].mean())
# 删除含有缺失值的行
data = data.dropna()
data.info()
# 将三分类变量转换为数值型变量
labels = data["Embarked"].unique().tolist()
data["Embarked"] = data["Embarked"].apply(lambda x: labels.index(x))
# 性别转换，astype可以将文本类转换为数字，将二分类特征转换为0、1
data["Sex"] = (data["Sex"] == "male").astype("int")

data.head()
# 提取特征矩阵X（排除标签列"Survived"）
X = data.iloc[:, data.columns != "Survived"]
# 查看X的前10行数据
X[:10]
y= data.iloc[:, data.columns == "Survived"]
y[:10]
from sklearn.model_selection import train_test_split
# 正确数据分割流程
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 仅使用训练集进行调参
X_train_sub, X_val, y_train_sub, y_val = train_test_split(X_train, y_train, test_size=0.25, random_state=42)

# 修正测试集和训练集的索引
for i in [Xtrain, Xtest, Ytrain, Ytest]:
    i.index = range(i.shape[0])

# 查看分好的训练集（可选，截图中有查看操作）
Xtrain.head()  
# 创建实例
clf = DecisionTreeClassifier(random_state=25)
# 训练模型
clf = clf.fit(Xtrain, Ytrain)
# 模型评分
score_ = clf.score(Xtest, Ytest)
score_
# 10折交叉验证
score = cross_val_score(clf, X, y, cv=10).mean()
score
# 选择决策树的深度
tr = []
te = []
# 遍历10次，每次修改树的深度，在每次分支时，不用全部特征，而是随机选取一部分特征，从中选取不纯度相关指标最优的作为分支用的结点 random_state
for i in range(10):
    clf = DecisionTreeClassifier(random_state=20,
                                 max_depth=i + 1,
                                 criterion="entropy"
                                 )
    clf = clf.fit(X, y)
    score_tr = clf.score(Xtrain, Ytrain)
    # 10折交叉验证
    score_te = cross_val_score(clf, X, y, cv=10).mean()
    tr.append(score_tr)
    te.append(score_te)
print(max(tr))
print(max(te))
# 绘制训练集和测试集得分随深度变化的折线图
plt.plot(range(1, 11), tr, color="red", label="train")
plt.plot(range(1, 11), te, color="blue", label="test")
# 坐标轴的单位
plt.xticks(range(1, 11))
plt.legend()
plt.show()
# 最优分数
print(GS.best_score_)#验证集最佳参数组合在交叉验证过程中的平均验证分数  它评估的是训练数据内部的泛化能力

ID3算法​

C4.5算法​